Cracking the AP Chemistry Exam

Part IV

Content Review for the AP Chemistry Exam

Chapter 5

Big Idea #3: Chemical Reactions, Energy Changes, and Redox Reactions

CHEMICAL EQUATIONS

Balancing Chemical Equations

Normally, balancing a chemical equation is a trial-and-error process. You start with the most complicated-looking compound in the equation and work from there. There is, however, an old Princeton Review SAT trick that you may want to try if you see a balancing equation question on the multiple-choice section. The trick is called backsolving.

It works like this: To make a balancing equation question work in a multiple-choice format, one of the answer choices is the correct coefficient for one of the species in the reaction. So instead of starting blind in the trial-and-error process, you can insert the answer choices one by one to see which one works. You probably won’t have to try all four, and if you start in the middle and the number doesn’t work, it might be obviously too small or large, eliminating other choices before you have to try them. Let’s try it.

…NH₃ +…O₂ →…N₂ +…H₂O

1. If the equation above were balanced with lowest whole number coefficients, the coefficient for NH₃ would be

(A) 1

(B) 2

(C) 3

(D) 4

A Note About
Backsolving

Backsolving is more
efficient than the methods
that you’re accustomed
to. If you use the answer
choices that you’re given,
you streamline the trial-
and-error process and allow
yourself to use POE as
you work on the problem.

Here’s How to Crack It!

Start at (C) because it’s the middle number. If there are 3NH₃’s, then there can’t be a whole number coefficient for N₂, so (C) is wrong, and so is the other odd number answer, (A).

Try (D).

If there are 4NH₃’s, then there must be 2N₂’s and 6H₂O’s.

If there are 6 H₂O’s, then there must be 3 O₂’s, and the equation is balanced with lowest whole number coefficients.

Chemical Equations and Calculations

Many of the stoichiometry problems on the test will be formatted in the following way: You will be given a balanced chemical equation and told that you have some number of grams (or liters of gas, or molar concentration, and so on) of reactant. Then you will be asked what number of grams (or liters of gas, or molar concentration, and so on) of products are generated.

In these cases, follow this simple series of steps.

1. Convert whatever quantity you are given into moles.

2. If you are given information about two reactants, you may have to use the equation coefficients to determine which one is the limiting reagent. Remember: The limiting reagent is not necessarily the reactant that you have the least of; it is the reactant that runs out first.

3. Use the balanced equation to determine how many moles of the desired product are generated.

4. Convert moles of product to the desired unit.

Let’s try one.

2 HBr(aq) + Zn(s) → ZnBr₂(aq) + H₂(g)

2. A piece of solid zinc weighing 98 grams was added to a solution containing 324 grams of HBr. What is the volume of H₂ produced at standard temperature and pressure if the reaction above runs to completion?

(A) 11 liters

(B) 22 liters

(C) 34 liters

(D) 45 liters

Here’s How to Crack It!

1. Convert whatever quantity you are given into moles.

Moles of Zn = 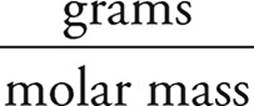= = 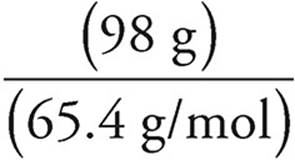1.5 mol

Moles of HBr = 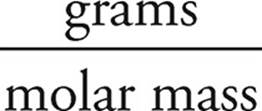= = 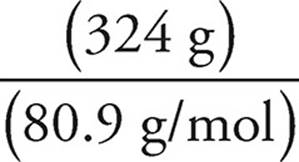4.0 mol

2. Use the balanced equation to find the limiting reagent. From the balanced equation, 2 moles of HBr are used for every mole of Zn that reacts, so when 1.5 moles of Zn react, 3 moles of HBr are consumed, and there will be HBr left over when all of the Zn is gone. That makes Zn the limiting reagent.

3. Use the balanced equation to determine how many moles of the desired product are generated.

1 mole of H₂ is produced for every mole of Zn consumed, so if 1.5 moles of Zn are consumed, then 1.5 moles of H₂ are produced.

4. Convert moles of product to the desired unit.

The H₂ gas is at STP, so we can convert directly from moles to volume.

Volume of H₂ = (moles)(22.4 L/mol) = (1.5 mol)(22.4 L/mol) = 33.6 L ≈ 34 L

So (C) is correct.

Let’s try another one using the same reaction.

2HBr(aq) + Zn(s) → ZnBr₂(aq) + H₂( g)

3. A piece of solid zinc weighing 13.1 grams was placed in a container. A 0.10-molar solution of HBr was slowly added to the container until the zinc was completely dissolved. What was the volume of HBr solution required to completely dissolve the solid zinc?

(A) 1.0 L

(B) 2.0 L

(C) 3.0 L

(D) 4.0 L

Here’s How to Crack It!

1. Convert whatever quantity you are given into moles.

Moles of Zn= 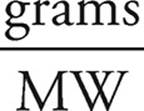= = 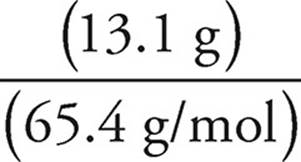0.200 mol

2. Use the balanced equation to find the limiting reagent.

3. Use the balanced equation to determine how many moles of the desired product are generated.

In this case, we’re using the balanced reaction to find out how much of one reactant is required to consume the other reactant.

We can see from the balanced equation that it takes 2 moles of HBr to react completely with 1 mole of Zn, so it will take 0.400 moles of HBr to react completely with 0.200 moles of Zn.

4. Convert moles of product to the desired unit.

Moles of HBr = (molarity)(volume)

Volume of HBr = 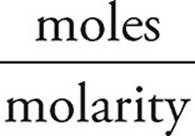= = 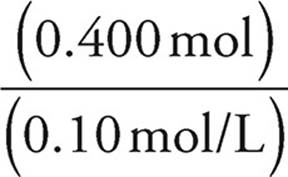4.0 L

So (D) is correct.

When you perform calculations, always include units. Including units in your calculations will help you (and the person scoring your test) keep track of what you are doing. While using the proper units in an answer is not typically worth any points in and of itself (with a few exceptions), AP graders may take off points if your units are missing or incorrect.