Cracking the AP Chemistry Exam
Part IV
Content Review for the AP Chemistry Exam
Chapter 6
Big Idea #4: Chemical Reactions and their Rates
CHAPTER 6 ANSWERS AND EXPLANATIONS
Multiple-Choice
1. D The answer to (A) shows all of the reactants and products that are part of this reaction. However, species that appear on both sides need to cancel. That eliminates B, one C, and D, leaving 2A + C → E
2. D Species B is a catalyst as it is present before before and after the reaction but cancels out of the overall equation. However, catalysts do not change the order of the reaction; they simply lower the activation energy so the reaction can proceed more quickly. The reaction would still take place without the catalyst, but it would proceed very slowly.
3. B The rate law for the slowest elementary step is also the overall rate law for the reaction. The rate law for any elementary step can be determined by taking the concentration of each reactant in that step and raising it to the power of any coefficient. Neither species A nor C has a coefficient in step 2, meaning they are both raised to the power of 1.
4. B Increasing the temperature increases the speed of the molecules. This will increase how often those molecules collide, meaning that a successful collision is more likely to happen. Additionally, there will also be more energy within each collision, making it more likely that the collision will exceed the activation energy barrier.
5. D While the rate of reaction may be increased by changing the concentration of A, the rate order, which describes how changing the concentration of A affects the speed of the reaction, will not change.
6. C To answer this we can do a unitless dimensional analysis:
M/s = k(M)(M)2
M/s = k(M)3
k = s−1M−2
7. B ; The coefficients on the reactants in the slowest elementary step match up with the order of those reactants in the overall rate law. However, B is an intermediate that is not present at the start of the reaction and as such cannot be part of the rate law. B is in equilibrium with 2A in the first step, though, so the 2A can be substituted for B in the slow step, which then yields choice (B) when the rate law is determined.
8. B For every two NO molecules that form, two NOCl molecules must disappear, so NO is appearing at the same rate that NOCl is disappearing. Choice (D) is wrong because for every mole of Cl2 that forms, two moles of NOCl are disappearing, so Cl2 is appearing at half the rate that NOCl is disappearing.
9. D From the rate law given in the question (Rate = k[H2][I2]), we can see that increasing the concentration of H2 will increase the rate of reaction. The rate constant, k, is not affected by changes in the concentration of the reactants.
10. A When temperature increases, the rate constant increases to reflect the fact that more reactant molecules are likely to have enough energy to react at any given time. So both the rate constant and the rate of reaction will increase.
11. C From a comparison of experiments 1 and 2, when [B] is doubled while [A] is held constant, the rate doubles. That means that the reaction is first order with respect to B.
From a comparison of experiments 2 and 3, when [A] is doubled while [B] is held constant, the rate doesn’t change. That means that the reaction is zero order with respect to A and that A will not appear in the rate law.
So the rate law is Rate = k[B].
12. D A spectrophotometer works by reading light absorbance. A red solution appears to be red because it transmits red light. The amount of light reflected by the solution does not change as it dilutes; the amount of light that is transmitted and absorbed does. The solution has a red color because the distance between the energy levels within the cobalt ions corresponds with the wavelength of red light.
13. D From a comparison of experiments 1 and 2, when [B] is doubled while [A] is held constant, the rate doubles. That means that the reaction is first order with respect to B.
From a comparison of experiments 2 and 3, when both [A] and [B] are doubled, the rate increases by a factor of 4. We would expect the rate to double based on the change in B; because the rate is in fact multiplied by 4, the doubling of A must also change the rate by a factor of 2, so the reaction is also first order with respect to A.
So the rate law is Rate = k[A][B].
14. A The key to this question is to recognize that reactant A is disappearing with a characteristic half-life. This is a signal that the reaction is first order with respect to A. So the rate law must be Rate = k[A].
15. D The reaction is a second order reaction, of which a graph of the inverse of concentration always produces a straight line with a slope equal to k, the rate constant.
16. B Make a chart. Always start at time = 0.
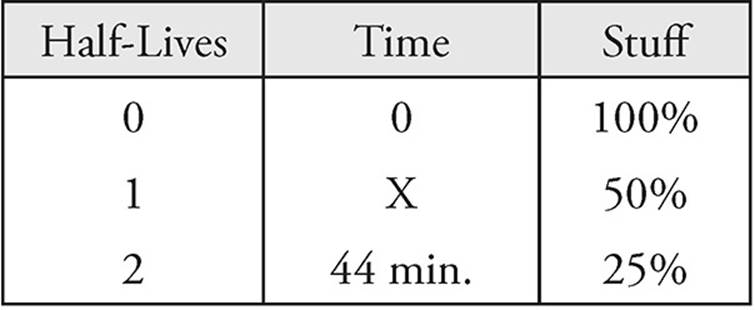
It takes two half-lives for the amount of  to decrease to 25 percent. If two half-lives takes 44 minutes, one half-life must be 22 minutes.
to decrease to 25 percent. If two half-lives takes 44 minutes, one half-life must be 22 minutes.
Free-Response
1. (a) When we compare the results of experiments 3 and 4, we see that when [A] doubles, the rate doubles, so the reaction is first order with respect to A.
When we compare the results of experiments 1 and 2, we see that when [B] doubles, the rate doubles, so the reaction is first order with respect to B.
Rate = k[A][B]
(b) Use the values from experiment 3, just because they look the simplest.
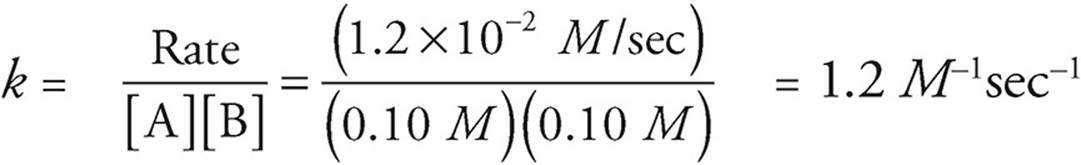
(c) Use the rate law.
Rate = k[A][B]
Rate = (1.2 M−1sec−1)(0.02 M)(0.02 M) = 4.8 × 10−4 M/sec
(d) (i) A + B → C + D
D + B → C
The two reactions add up to
A + 2B + D → 2C + D
D’s cancel, and we’re left with the balanced equation.
A + 2B → 2C
(ii) A + B → C + D (slow)
D + B → C (fast)
The first part of the mechanism is the slow, rate-determining step because its rate law is the same as the experimentally determined rate law.
2. (a) When we compare the results of experiments 1 and 2, we see that when [NO] doubles, the rate quadruples, so the reaction is second order with respect to NO.
When we compare the results of experiments 1 and 3, we see that when [Br2] doubles, the rate doubles, so the reaction is first order with respect to Br2.
Rate = k[NO]2[Br2]
(b) Use the values from experiment 1, just because they look the simplest.
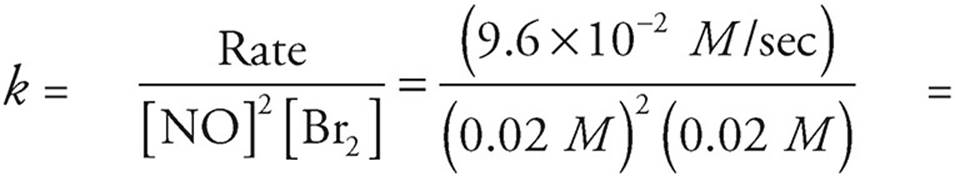
1.2 × 104 M−2 sec−1
(c) In experiment 2, we started with [Br2] = 0.02 M, so 0.01 M was consumed.
From the balanced equation, 2 moles of NO are consumed for every mole of Br2 consumed. So 0.02 M of NO are consumed.
[NO] remaining = 0.04 M − 0.02 M = 0.02 M
(d) Choice (I) agrees with the rate law.
NO + NO ↔ N2O2 (fast)
N2O2 + Br2 → 2NOBr (slow)
The slow step is the rate-determining step, with the following rate law:
Rate = k[N2O2][Br2]
Looking at the first step in the proposed mechanism, we can replace the N2O2 with 2NO. Doing so gives us:
2NO + Br2 → 2NOBr
The rate law for that elementary step matches the overall rate law determined previously.
3. (a) Use the first-order rate law and insert the first two lines from the table.
ln[N2O5]t − ln[N2O5]0 = −kt
ln(0.289) − ln(0.400) = −k(20.0 min)
−.325 = −k(20.0 min)
k = 0.0163 min−1
(b) Use the first-order rate law.
ln[N2O5]t − ln[N2O5]0 = −kt
ln(0.350) − ln(0.400) = −(0.0163 min−1)t
−0.134 = −(0.0163 min−1)t
t = 8.22 min
(c) Use the first-order rate law.
ln[N2O5] − ln[N2O5]0 = −kt
ln[N2O5] − ln(0.400) = −(0.0163 min−1)(100 min)
ln[N2O5] + 0.916 = 1.63
ln[N2O5] = −2.55
[N2O5] = e−2.55 M = 0.078 M
(d) For a first-order reaction, Rate = k[N2O5] = (0.0163 min−1)(0.400 M) = 0.00652 M/min
(e) You can see from the numbers on the table that the half-life is slightly over 40 min. To calculate it exactly, use the formula Half-life = 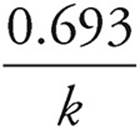 =
= 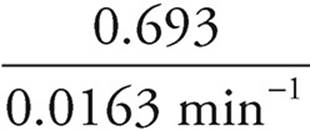 = 42.5 min
= 42.5 min
4. (a) (i) The reaction is first order. The half-life is constant; it takes 40 seconds for the concentration to drop from 0.20 M to 0.10 M, and another 40 seconds for it to drop from 0.10 M to 0.050 M. This type of exponential decay is typical of a first order reaction.
(ii) After t = 80 s, another 40 seconds is an additional half-life, and it would bring the concentration down to 0.025 M (half of 0.050 M)
(b) (i) We can use the stoichiometric ratios to determine the rate of appearance of P4:
2.5 × 10−3 M/s PH3 × 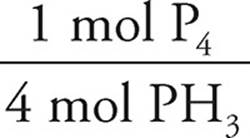 = 6.3 × 10−4 M/s P4
= 6.3 × 10−4 M/s P4
(ii) As the reaction progresses, the rate at which the phosphine disappears will decrease, as indicated by the decreasing slope of the line. Thus, the rate of appearance of P4 will also decrease.
(c) (i) The half-life of the phosphine will decrease. This is because at a higher temperature, the reaction will proceed faster. It will thus take less time for the phosphine to decay.
(ii) The rate law is unaffected by outside conditions and will remain unchanged.
(iii) The rate constant will increase. There is a directly proportional relationship between rate constant and temperature. As the temperature increases, so will the rate constant.
5. (a) The rate of the reaction will increase because the rate depends on the concentration of A as given in the rate law: Rate = k[A]2.
The rate constant is independent of the concentration of the reactants and will not change.
(b) The rate of the reaction will not change. If the reaction is zero order with respect to B, then the rate is independent of the concentration of B.
The rate constant is independent of the concentration of the reactants and will not change.
(c) The rate of the reaction will increase with increasing temperature because the rate constant increases with increasing temperature.
The rate constant increases with increasing temperature because at a higher temperature more gas molecules will collide with enough energy to overcome the activation energy for the reaction.
(d) Neither the rate nor the rate constant will be affected by the addition of an inert gas.
(e) The rate of the reaction will increase because decreasing the volume of the container will increase the concentration of A. Rate = k[A]2
The rate constant is independent of the concentration of the reactants and will not change.
6. (a) Line 2 is the catalyzed reaction. Adding a catalyst lowers the activation energy of the reaction, making it easier for the reaction to occur.
(b) Line 2 shows the higher temperature distribution. At a higher temperature, more of the molecules will be at higher energies, causing the distribution to flatten out and shift to the right.
(c) Line 1 is correct. ln[reactant] for a first order reaction changes in a linear fashion over time, as shown in the following equation.
ln[A]t = kt + ln[A]0
y = mx + b
Notice the similarity to the slope-intercept form for a linear equation.
(d) Graph 1 is correct, showing a decrease in the concentration of A as it is consumed in the reaction and a corresponding increase in the concentration of B as it is produced.
7. (a) An increase in temperature means an increase in the energy of the molecules present. If the molecules have more energy, then more of them will collide more often with enough energy to overcome the activation energy required for a reaction to take place, causing the reaction to proceed more quickly.
(b) A catalyst offers a reaction an alternative pathway with a lower activation energy. If the activation energy is lowered, then more molecular collisions will occur with enough energy to overcome the activation energy, causing the reaction to proceed more quickly.
(c) The effectiveness of a solid catalyst depends on the surface area of the catalyst that is exposed to the reactants. Grinding a solid into powder greatly increases its surface area.
(d) Increasing the concentration of reactants crowds the reactants more closely together, making it more likely that they will collide with one another. The more collisions that occur, the more likely that collisions that will result in reactions will occur.
8. (a) (i)  = 2.0 × 10−7 M/s
= 2.0 × 10−7 M/s
(ii) The solution starts reacting (and thus, fading) immediately after it is mixed. If the student waited 30 seconds before putting the cuvette in, the calculated rate of disappearance would thus decrease.
(b) A = abc
A = (26,000 cm/M)(1.00 cm)(3.8 × 10−5 M)
A = 0.98
(c) A reaction that is first order with respect to [CV+] will create a straight line in a graph of ln [CV+] vs. time.

(d) Between trials 1 and 2, the value of the [CV+] remained constant while the [OH−] doubled. At the same time, the rate of reaction also doubled, meaning there is a direct relationship between [OH−] and the rate, so the reaction is first order with respect to [OH−]. The rate with respect to [CV+] has already been established as first order, so:
rate = k[CV+][OH−]
(e) Either of the trials can be used for this. Taking trial 2:
7.20 × 10−7 M/s = k(5.5 × 10−5 M)(0.24 M)
k = 0.055 M−1s−1
(f) rate = k[CV+][OH−]
rate = (0.055 M−1s−1)(4.1 × 10−5 M)(0.18 M)
rate = 4.1 × 10−7 s−1