CHEMISTRY THE CENTRAL SCIENCE
13 PROPERTIES OF SOLUTIONS
13.5 COLLIGATIVE PROPERTIES
Some physical properties of solutions differ in important ways from those of the pure solvent. For example, pure water freezes at 0 °C, but aqueous solutions freeze at lower temperatures. We utilize this behavior when we add ethylene glycol antifreeze to a car's radiator to lower the freezing point of the solution. The added solute also raises the boiling point of the solution above that of pure water, making it possible to operate the engine at a higher temperature.
Lowering of the freezing point and raising of the boiling point are physical properties of solutions that depend on the quantity (concentration) but not the kind or identity of the solute particles. Such properties are called colligative properties. (Colligative means “depending on the collection”; colligative properties depend on the collective effect of the number of solute particles.)
In addition to freezing-point lowering and boiling-point raising, vapor-pressure lowering and osmotic pressure are also colligative properties. As we examine each one, notice how solute concentration quantitatively affects the property.
Vapor-Pressure Lowering
A liquid in a closed container establishes equilibrium with its vapor. 
(Section 11.5) The vapor pressure is the pressure exerted by the vapor when it is at equilibrium with the liquid (that is, when the rate of vaporization equals the rate of condensation). A substance that has no measurable vapor pressure is nonvolatile, whereas one that exhibits a vapor pressure is volatile.
A solution consisting of a volatile liquid solvent and a nonvolatile solute forms spontaneously because of the increase in entropy that accompanies their mixing. In effect, the solvent molecules are stabilized in their liquid state by this process and thus have a lower tendency to escape into the vapor state. Therefore, when a nonvolatile solute is present, the vapor pressure of the solvent is lower than the vapor pressure of the pure solvent, as illustrated in 
FIGURE 13.21.
The vapor pressure of a volatile solvent above a solution containing a nonvolatile solute is proportional to the solvent's concentration in the solution. This relationship is expressed quantitatively by Raoult's law, which states that the partial pressure exerted by solvent vapor above the solution, Psolution, equals the product of the mole fraction of the solvent, Xsolvent, times the vapor pressure of the pure solvent, P°solvent:
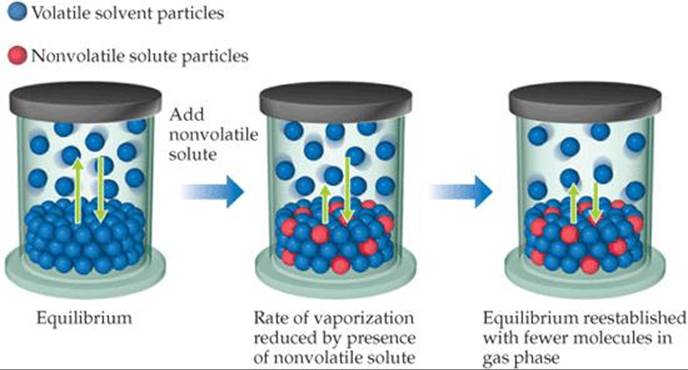
FIGURE 13.21 Vapor-pressure lowering. The presence of nonvolatile solute particles in a liquid solvent results in a reduction of the vapor pressure above the liquid.
For example, the vapor pressure of pure water at 20 °C is P°H2O = 17.5 torr. Imagine holding the temperature constant while adding glucose (C6H12O6) to the water so that the mole fractions in the resulting solution are XH2O = 0.800 and XC6H12O6 = 0.200. According to Equation 13.10, the vapor pressure of the water above this solution is 80.0% of that of pure water:
Psolution = (0.800)(17.5 torr) = 14.0 torr
The presence of the nonvolatile solute lowers the vapor pressure of the volatile solvent by 17.5 torr – 14.0 torr = 3.5 torr.
The vapor-pressure lowering, ΔP, is directly proportional to the mole fraction of the solute, Xsolute:
Thus, for the example of the solution of glucose in water, we have
The vapor-pressure lowering caused by adding a nonvolatile solute depends on the total concentration of solute particles, regardless of whether they are molecules or ions. Remember that vapor-pressure lowering is a colligative property, so its value for any solution depends on the concentration of solute particles and not on their kind or on their identity.
GIVE IT SOME THOUGHT
Adding 1 mol of NaCl to 1 kg of water lowers the vapor pressure of water more than adding 1 mol of C6H12O6. Explain.
SAMPLE EXERCISE 13.7 Calculation of Vapor Pressure of a Solution
Glycerin (C3H8O3) is a nonvolatile nonelectrolyte with a density of 1.26 g/mL at 25 °C. Calculate the vapor pressure at 25 °C of a solution made by adding 50.0 mL of glycerin to 500.0 mL of water. The vapor pressure of pure water at 25 °C is 23.8 torr (Appendix B), and its density is 1.00 g/mL.
SOLUTION
Analyze Our goal is to calculate the vapor pressure of a solution, given the volumes of solute and solvent and the density of the solute.
Plan We can use Raoult's law (Equation 13.10) to calculate the vapor pressure of a solution. The mole fraction of the solvent in the solution, Xsolvent, is the ratio of the number of moles of solvent (H2O) to total moles of solution (moles C3H8O3 + moles H2O).
Solve To calculate the mole fraction of water in the solution, we must determine the number of moles of C3H8O3 and H2O:
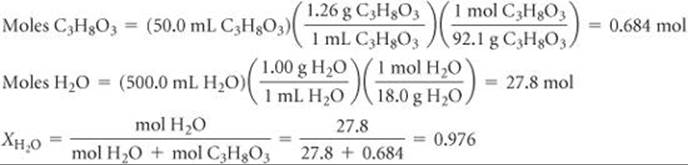
We now use Raoult's law to calculate the vapor pressure of water for the solution:
Comment The vapor pressure of the solution has been lowered by 23.8 torr – 23.2 torr = 0.6 torr relative to that of pure water. The vapor-pressure lowering can be calculated directly using Equation 13.11 together with the mole fraction of the solute, C3H8O3: ΔP = XC3H8O3P°H2O = (0.024)(23.8 torr) = 0.57 torr. Notice that the use of Equation 13.11 gives one more significant figure than the number obtained by subtracting the vapor pressure of the solution from that of the pure solvent.
PRACTICE EXERCISE
The vapor pressure of pure water at 110 °C is 1070 torr. A solution of ethylene glycol and water has a vapor pressure of 1.00 atm at 110 °C. Assuming that Raoult's law is obeyed, what is the mole fraction of ethylene glycol in the solution?
Answer: 0.290
A CLOSER LOOK
IDEAL SOLUTIONS WITH TWO OR MORE VOLATILE COMPONENTS
Solutions sometimes have two or more volatile components. Gasoline, for example, is a solution of several volatile liquids. To gain some understanding of such mixtures, consider an ideal solution of two volatile liquids, A and B. (For our purposes here, it does not matter which we call the solute and which the solvent.) The partial pressures above the solution are given by Raoult's law:
and the total vapor pressure above the solution is
Consider a mixture of 1.0 mol of benzene (C6H6) and 2.0 mol of toluene (C7H8) (Xben = 0.33, Xtol = 0.67). At 20 °C the vapor pressures of the pure substances are P°ben = 75 torr and P°tol = 22 torr. Thus, the partial pressures above the solution are
and the total vapor pressure above the liquid is
Note that the vapor is richer in benzene, the more volatile component.
The mole fraction of benzene in the vapor is given by the ratio of its vapor pressure to the total pressure (Equations 10.14 and 10.15):
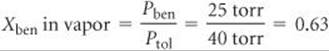
Although benzene constitutes only 33% of the molecules in the solution, it makes up 63% of the molecules in the vapor.
When an ideal liquid solution containing two volatile components is in equilibrium with its vapor, the more volatile component will be relatively richer in the vapor. This fact forms the basis of distillation, a technique used to separate (or partially separate) mixtures containing volatile components. Distillation is the procedure by which a moonshiner obtains whiskey using a still and by which petrochemical plants achieve the separation of crude petroleum into gasoline, diesel fuel, lubricating oil, and so forth (
FIGURE 13.22). Distillation is also used routinely on a small scale in the laboratory.
RELATED EXERCISES: 13.67, 13.68
FIGURE 13.22 The volatile components of organic mixtures can be separated on an industrial scale.
An ideal gas is defined as one that obeys the ideal-gas equation (Section 10.4), and an ideal solution is defined as one that obeys Raoult's law. Whereas ideality for a gas arises from a complete lack of intermolecular interaction, ideality for a solution implies total uniformity of interaction. The molecules in an ideal solution all influence one another in the same way—in other words, solute–solute, solvent–solvent, and solute–solvent interactions are indistinguishable from one another. Real solutions best approximate ideal behavior when the solute concentration is low and solute and solvent have similar molecular sizes and take part in similar types of intermolecular attractions.
Many solutions do not obey Raoult's law exactly and so are not ideal. If, for instance, the solvent–solute interactions in a solution are weaker than either the solvent–solvent or solute–solute interactions, the vapor pressure tends to be greater than predicted by Raoult's law (that is, the vapor-pressure lowering is less than what Raoult's law predicts). When the solute–solvent interactions in a solution are exceptionally strong, as might be the case when hydrogen bonding exists, the vapor pressure is lower than Raoult's law predicts (the vapor-pressure lowering is greaterthan what the law predicts). Although you should be aware that these departures from ideality occur, we will ignore them for the remainder of this chapter.
Boiling-Point Elevation
In Sections 11.5 and 11.6 we examined the vapor pressures of pure substances and how to use them to construct phase diagrams. How does the phase diagram of a solution and, hence, its boiling and freezing points differ from that of the pure solvent? The addition of a nonvolatile solute lowers the vapor pressure of the solution. Thus, in 
FIGURE 13.23 the vapor-pressure curve of the solution is shifted downward relative to the vapor-pressure curve of the pure solvent.
Recall from Section 11.5 that the normal boiling point of a liquid is the temperature at which its vapor pressure equals 1 atm. Because the solution has a lower vapor pressure than the pure solvent, a higher temperature is required for the solution to achieve a vapor pressure of 1 atm. As a result, the boiling point of the solution is higher than that of the pure solvent. This effect is seen in Figure 13.23. We find the normal boiling points of the pure solvent from the graph by locating the point where the horizontal line at 1 atm intersects the black vapor-pressure curve and then tracing this point down to the temperature axis. For the solution, the horizontal line at 1 atm intersects the blue vapor-pressure curve at a higher temperature, indicating that the solution has a higher boiling point than the pure solvent.
The increase in boiling point relative to that of the pure solvent, ΔTb, is a positive quantity obtained by subtracting the boiling point of the pure solvent from the boiling point of the solution. The value of ΔTb is directly proportional to the solution molality:
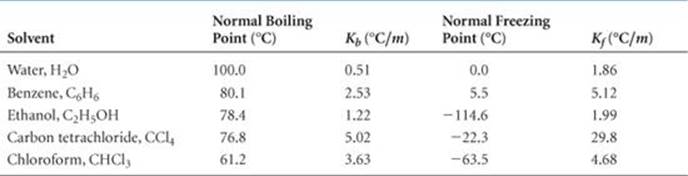
The magnitude of Kb, which is called the molal boiling-point-elevation constant, depends only on the solvent. Some typical values for several common solvents are given in 
TABLE 13.3. For water, the table shows Kb = 0.51 °C/m, which means that the boiling point of any aqueous solution that is 1 m in nonvolatile solute particles is 0.51 °C higher than the boiling point of pure water. Because solutions generally do not behave ideally, the constants listed in Table 13.3 serve well only for solutions that are not too concentrated.
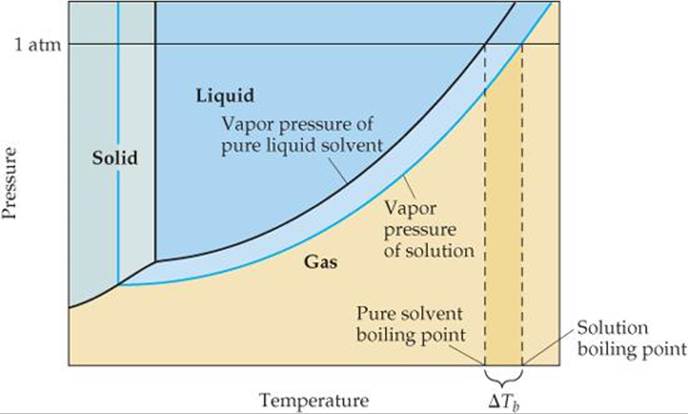
FIGURE 13.23 Phase diagram illustrating boiling-point elevation.
TABLE 13.3 • Molal Boiling-Point-Elevation and Freezing-Point-Depression Constants
It is important to remember that boiling-point elevation is proportional to the total concentration of solute particles, regardless of whether the particles are molecules or ions. When NaCl dissolves in water, 2 mol of solute particles (1 mol of Na+ and 1 mol of Cl–) are formed for each mole of NaCl that dissolves. Therefore, a 1 m aqueous solution of NaCl is 1 m in Na+ and 1 m in Cl–, making it 2 m in total solute particles. As a result, the boiling-point elevation of a 1 m aqueous solution of NaCl is approximately (2 m)(0.51 °C/m) = 1 °C, twice as large as the boiling-point elevation of a 1 m solution of a nonelectrolyte such as sucrose. Thus, to properly predict the effect of a particular solute on boiling-point elevation (or any other colligative property), it is important to know whether the solute is an electrolyte or a nonelectrolyte. (Sections 4.1 and 4.3)
GIVE IT SOME THOUGHT
A solute dissolved in water causes the boiling point to increase by 0.51 °C. Does this necessarily mean that the concentration of the solute is 1.0 m?
Freezing-Point Depression
The vapor-pressure curves for the liquid and solid phases meet at the triple point. (Section 11.6) In FIGURE 13.24 we see that the triple-point temperature of the solution is lower than the triple-point temperature of pure liquid because the solution has a lower vapor pressure than the pure liquid.
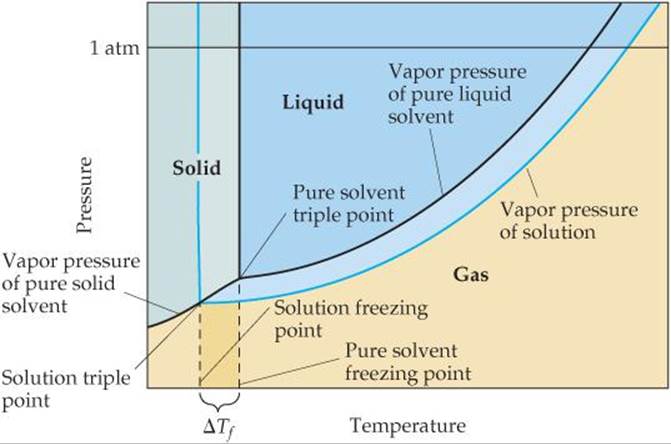
FIGURE 13.24 Phase diagram illustrating freezing-point depression.
The freezing point of a solution is the temperature at which the first crystals of pure solvent form in equilibrium with the solution. Recall from Section 11.6 that the line representing the solid–liquid equilibrium rises nearly vertically from the triple point. Because the triple-point temperature of the solution is lower than that of the pure liquid, the freezing point of the solution is lower than that of the pure liquid. The decrease in freezing point, ΔTf, is a positive quantity obtained by subtracting the freezing point of the solution from the freezing point of the pure solvent.
Like the boiling-point elevation, ΔTf is directly proportional to solute molality:
The values of Kf, the molal freezing-point-depression constant, for several common solvents are given in Table 13.3. For water, Kf is 1.86 °C/m. Therefore, any aqueous solution that is 1 m in nonvolatile solute particles (such as 1 m C6H12O6 or 0.5 m NaCl) freezes at the temperature that is 1.86 °C lower than the freezing point of pure water.
The freezing-point depression caused by solutes explains the use of antifreeze in cars and the use of calcium chloride (CaCl2) to melt ice on roads during winter.
SAMPLE EXERCISE 13.8 Calculation of Boiling-Point Elevation and Freezing-Point Depression
Automotive antifreeze consists of ethylene glycol, CH2(OH)CH2(OH), a nonvolatile nonelectrolyte. Calculate the boiling point and freezing point of a 25.0 mass % solution of ethylene glycol in water.
SOLUTION
Analyze We are given that a solution contains 25.0 mass % of a nonvolatile, nonelectrolyte solute and asked to calculate the boiling and freezing points of the solution. To do this, we need to calculate the boiling-point elevation and freezing-point depression.
Plan To calculate the boiling-point elevation and the freezing-point depression using Equations 13.12 and 13.13, we must express the concentration of the solution as molality. Let's assume for convenience that we have 1000 g of solution. Because the solution is 25.0 mass % ethylene glycol, the masses of ethylene glycol and water in the solution are 250 and 750 g, respectively. Using these quantities, we can calculate the molality of the solution, which we use with the molal boiling-point-elevation and freezing-point-depression constants (Table 13.3) to calculate ΔTb and ΔTf. We add ΔTb to the boiling point and subtract ΔTf from the freezing point of the solvent to obtain the boiling point and freezing point of the solution.
Solve The molality of the solution is calculated as follows:
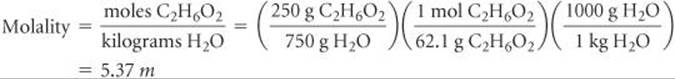
We can now use Equations 13.12 and 13.13 to calculate the changes in the boiling and freezing points:
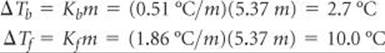
Hence, the boiling and freezing points of the solution are
Comment Notice that the solution is a liquid over a larger temperature range than the pure solvent.
PRACTICE EXERCISE
Calculate the freezing point of a solution containing 0.600 kg of CHCl3 and 42.0 g of eucalyptol (C10H18O), a fragrant substance found in the leaves of eucalyptus trees. (See Table 13.3.)
Answer: –65.6 °C
SAMPLE EXERCISE 13.9 Freezing-Point Depression in Aqueous Solutions
List the following aqueous solutions in order of their expected freezing point: 0.050 m CaCl2, 0.15 m NaCl, 0.10 m HCl, 0.050 m CH3COOH, 0.10 m C12H22O11.
SOLUTION
Analyze We must order five aqueous solutions according to expected freezing points, based on molalities and the solute formulas.
Plan The lowest freezing point will correspond to the solution with the greatest concentration of solute particles. To determine the total concentration of solute particles in each case, we must determine whether the substance is a nonelectrolyte or an electrolyte and consider the number of ions formed when an electrolyte ionizes.
Solve CaCl2, NaCl, and HCl are strong electrolytes, CH3COOH (acetic acid) is a weak electrolyte, and C12H22O11 is a nonelectrolyte. The molality of each solution in total particles is as follows:
Because the freezing points depend on the total molality of particles in solution, the expected ordering is 0.15 m NaCl (lowest freezing point), 0.10 m HCl, 0.050 m CaCl2, 0.10 m C12H22O11, and 0.050 m CH3COOH (highest freezing point).
PRACTICE EXERCISE
Which of the following solutes will produce the largest increase in boiling point upon addition to 1 kg of water: 1 mol of Co(NO3)2, 2 mol of KCl, 3 mol of ethylene glycol (C2H6O2)?
Answer: 2 mol of KCl because it contains the highest concentration of particles, 2 m K+ and 2 m Cl–, giving 4 m in all
Osmosis
Certain materials, including many membranes in biological systems and synthetic substances such as cellophane, are semipermeable. When in contact with a solution, these materials allow only small molecules—water molecules, for instance—to pass through their network of tiny pores.
Consider a situation in which only solvent molecules are able to pass through a semipermeable membrane placed between two solutions of different concentrations. The rate at which the solvent passes from the less concentrated solution (lower solute concentration but higher solvent concentration) to the more concentrated solution (higher solute concentration but lower solvent concentration) is greater than the rate in the opposite direction. Thus, there is a net movement of solvent molecules from the solution with a lower solute concentration into the one with a higher solute concentration. In this process, called osmosis, the net movement of solvent is always toward the solution with the higher solute concentration, as if the solutions were driven to attain equal concentrations.
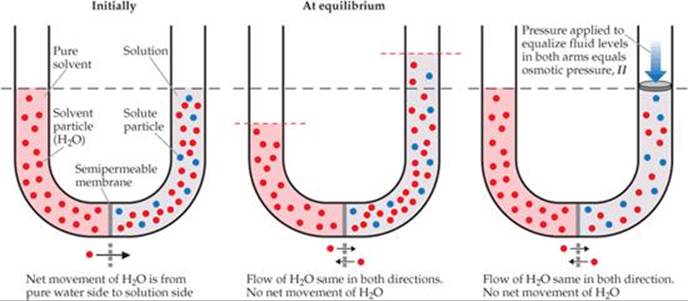
FIGURE 13.25 shows the osmosis that occurs between an aqueous solution and pure water. The U-tube contains water on the left and an aqueous solution on the right. There is a net movement of water through the membrane from left to right, As a result, the liquid levels in the two arms become unequal. Eventually, the pressure difference resulting from the unequal liquid heights becomes so large that the net flow of water ceases. The pressure required to stop osmosis from a pure solvent to a solution is the osmotic pressure of the solution. If an external pressure equal to the osmotic pressure is applied to the solution, the liquid levels in the two arms can be equalized, as shown in the right panel of Figure 13.25.
GO FIGURE
If the pure water in the left arm of the U-tube is replaced by a solution more concentrated than the one in the right arm, what will happen?
FIGURE 13.25 Osmosis.
The osmotic pressure obeys a law similar in form to the ideal-gas law, ΠV = nRT, where Π is the osmotic pressure, V is the volume of the solution, n is the number of moles of solute, R is the ideal-gas constant, and T is the Kelvin temperature. From this equation, we can write
where M is the molarity of the solution. Because the osmotic pressure for any solution depends on the solution concentration, osmotic pressure is a colligative property.
If two solutions of identical osmotic pressure are separated by a semipermeable membrane, no osmosis will occur. The two solutions are isotonic with respect to each other. If one solution is of lower osmotic pressure, it is hypotonic with respect to the more concentrated solution. The more concentrated solution is hypertonic with respect to the dilute solution.
GIVE IT SOME THOUGHT
Of two KBr solutions, one 0.50 m and the other 0.20 m, which is hypotonic with respect to the other?
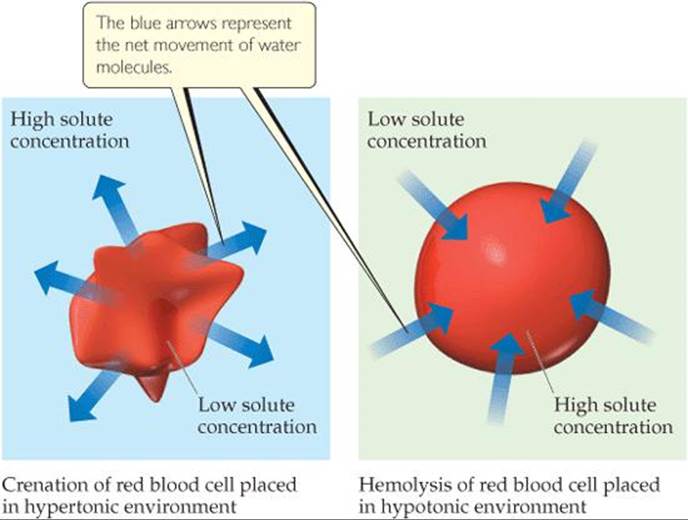
Osmosis plays an important role in living systems. The membranes of red blood cells, for example, are semipermeable. Placing a red blood cell in a solution that is hypertonic relative to the intracellular solution (the solution inside the cells) causes water to move out of the cell (FIGURE 13.26). This causes the cell to shrivel, a process called crenation. Placing the cell in a solution that is hypotonic relative to the intracellular fluid causes water to move into the cell. This may cause the cell to rupture, a process called hemolysis. People who need body fluids or nutrients replaced but cannot be fed orally are given solutions by intravenous (IV) infusion, which feeds nutrients directly into the veins. To prevent crenation or hemolysis of red blood cells, the IV solutions must be isotonic with the intracellular fluids of the blood cells.
GO FIGURE
If the fluid surrounding a patient's red blood cells is depleted in electrolytes, is crenation or hemolysis more likely to occur?
FIGURE 13.26 Osmosis through red blood cell wall.
SAMPLE EXERCISE 13.10 Calculation Involving Osmotic Pressure
The average osmotic pressure of blood is 7.7 atm at 25 °C. What molarity of glucose (C6H12O6) will be isotonic with blood?
SOLUTION
Analyze We are asked to calculate the concentration of glucose in water that would be isotonic with blood, given that the osmotic pressure of blood at 25 °C is 7.7 atm.
Plan Because we are given the osmotic pressure and temperature, we can solve for the concentration, using Equation 13.14.
Solve
Comment In clinical situations the concentrations of solutions are generally expressed as mass percentages. The mass percentage of a 0.31 M solution of glucose is 5.3%. The concentration of NaCl that is isotonic with blood is 0.16 M, because NaCl ionizes to form two particles, Na+ and Cl–(a 0.155 M solution of NaCl is 0.310 M in particles). A 0.16 M solution of NaCl is 0.9 mass % in NaCl. This kind of solution is known as a physiological saline solution.
PRACTICE EXERCISE
What is the osmotic pressure at 20 °C of a 0.0020 M sucrose (C12H22O11) solution?
Answer: 0.048 atm, or 37 torr
There are many interesting biological examples of osmosis. A cucumber placed in concentrated brine loses water via osmosis and shrivels into a pickle. People who eat a lot of salty food retain water in tissue cells and intercellular space because of osmosis. The resultant swelling or puffiness is called edema. Water moves from soil into plant roots partly because of osmosis. Bacteria on salted meat or candied fruit lose water through osmosis, shrivel, and die—thus preserving the food.
Movement of a substance from an area where its concentration is high to an area where it is low is spontaneous. Biological cells transport water and other select materials through their membranes, permitting nutrients to enter and waste materials to exit. In some cases substances must be moved across the cell membrane from an area of low concentration to one of high concentration. This movement—called active transport—is not spontaneous, so cells must expend energy to do it.
GIVE IT SOME THOUGHT
Is the osmotic pressure of a 0.10 M solution of NaCl greater than, less than, or equal to that of a 0.10 M solution of KBr?
Determination of Molar Mass
The colligative properties of solutions provide a useful means of determining molar mass. Any of the four colligative properties can be used, as shown in Sample Exercises 13.11 and 13.12.
SAMPLE EXERCISE 13.11 Molar Mass from Freezing-Point Depression
A solution of an unknown nonvolatile nonelectrolyte was prepared by dissolving 0.250 g of the substance in 40.0 g of CCl4. The boiling point of the resultant solution was 0.357 °C higher than that of the pure solvent. Calculate the molar mass of the solute.
SOLUTION
Analyze Our goal is to calculate the molar mass of a solute based on knowledge of the boiling-point elevation of its solution in CCl4, ΔTb = 0.357 °C, and the masses of solute and solvent. Table 13.3 gives Kb for the solvent (CCl4), Kb = 5.02 °C/m.
Plan We can use Equation 13.12, ΔTb = Kbm, to calculate the molality of the solution. Then we can use molality and the quantity of solvent (40.0 g CCl4) to calculate the number of moles of solute. Finally, the molar mass of the solute equals the number of grams per mole, so we divide the number of grams of solute (0.250 g) by the number of moles we have just calculated.
Solve From Equation 13.12 we have
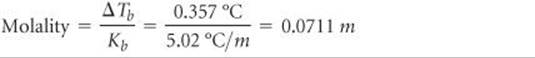
Thus, the solution contains 0.0711 mol of solute per kilogram of solvent. The solution was prepared using 40.0 g = 0.0400 kg of solvent (CCl4). The number of moles of solute in the solution is therefore
The molar mass of the solute is the number of grams per mole of the substance:
PRACTICE EXERCISE
Camphor (C10H16O) melts at 179.8 °C, and it has a particularly large freezing-point-depression constant, Kf = 40.0 °C/m. When 0.186 g of an organic substance of unknown molar mass is dissolved in 22.01 g of liquid camphor, the freezing point of the mixture is found to be 176.7 °C. What is the molar mass of the solute?
Answer: 110 g/mol
SAMPLE EXERCISE 13.12 Molar Mass from Osmotic Pressure
The osmotic pressure of an aqueous solution of a certain protein was measured to determine the protein's molar mass. The solution contained 3.50 mg of protein dissolved in sufficient water to form 5.00 mL of solution. The osmotic pressure of the solution at 25 °C was found to be 1.54 torr. Treating the protein as a nonelectrolyte, calculate its molar mass.
SOLUTION
Analyze Our goal is to calculate the molar mass of a high-molecular-mass protein, based on its osmotic pressure and a knowledge of the mass of protein and solution volume.
Plan The temperature (T = 25 °C) and osmotic pressure (Π = 1.54 torr) are given, and we know the value of R so we can use Equation 13.14 to calculate the molarity of the solution, M. In doing so, we must convert temperature from °C to K and the osmotic pressure from torr to atm. We then use the molarity and the volume of the solution (5.00 mL) to determine the number of moles of solute. Finally, we obtain the molar mass by dividing the mass of the solute (3.50 mg) by the number of moles of solute.
Solve Solving Equation 13.14 for molarity gives
Because the volume of the solution is 5.00 mL = 5.00 × 10–3 L, the number of moles of protein must be
Moles = (8.28 × 10–5 mol/L)(5.00 × 10–3 L) = 4.14 × 10–7 mol
The molar mass is the number of grams per mole of the substance. The sample has a mass of 3.50 mg = 3.50 × 10–3 g. The molar mass is the number of grams divided by the number of moles:
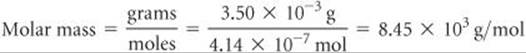
Comment Because small pressures can be measured easily and accurately, osmotic pressure measurements provide a useful way to determine the molar masses of large molecules.
PRACTICE EXERCISE
A sample of 2.05 g of polystyrene of uniform polymer chain length was dissolved in enough toluene to form 0.100 L of solution. The osmotic pressure of this solution was found to be 1.21 kPa at 25 °C. Calculate the molar mass of the polystyrene.
Answer: 4.20 × 104 g/mol
A CLOSER LOOK
COLLIGATIVE PROPERTIES OF ELECTROLYTE SOLUTIONS
The colligative properties of solutions depend on the total concentration of solute particles, regardless of whether the particles are ions or molecules. Thus, we expect a 0.100 m solution of NaCl to have a freezing-point depression of (0.200 m)(1.86 °C/m) = 0.372 °C because it is 0.100 m in Na+(aq) and 0.100 m in Cl–(aq). The measured freezing-point depression is only 0.348 °C, however, and the situation is similar for other strong electrolytes. A 0.100 m solution of KCl, for example, freezes at –0.344 °C.
The difference between expected and observed colligative properties for strong electrolytes is due to electrostatic attractions between ions. As the ions move about in solution, ions of opposite charge collide and “stick together” for brief moments. While they are together, they behave as a single particle called an ion pair (FIGURE 13.27). The number of independent particles is thereby reduced, causing a reduction in the freezing-point depression (as well as in boiling-point elevation, vapor-pressure reduction, and osmotic pressure).
One measure of the extent to which electrolytes dissociate is the van't Hoff factor, i. This factor is the ratio of the actual value of a colligative property to the value calculated when the substance is assumed to be a nonelectrolyte. Using the freezing-point depression, for example, we have
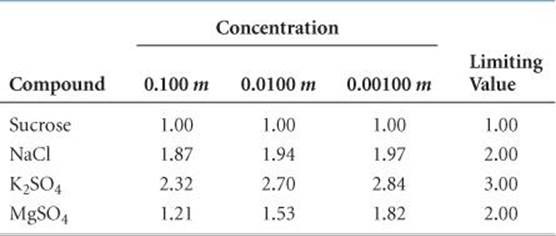
The limiting value of i can be determined for a salt from the number of ions per formula unit. For NaCl, for example, the limiting van't Hoff factor is 2 because NaCl consists of one Na+ and one Cl– per formula unit; for K2SO4 it is 3 because K2SO4 consists of two K+ and one SO42– per formula unit. In the absence of any information about the actual value of i for a solution, we will use the limiting value in calculations.
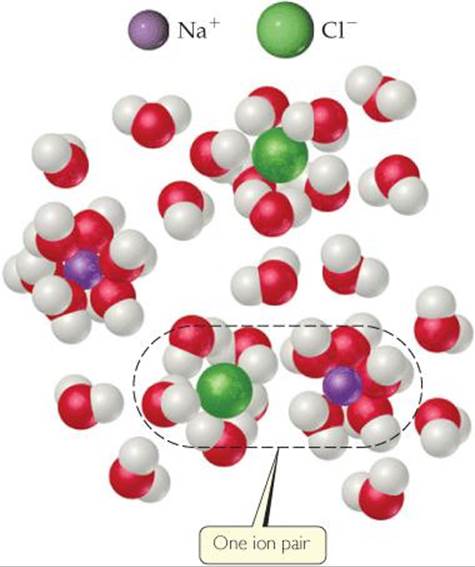
FIGURE 13.27 Ion pairing and colligative properties. A solution of NaCl contains not only separated Na+(ag) and Cl–(aq) ions but ion pairs as well.
Two trends are evident in 
TABLE 13.4, which gives measured van't Hoff factors for several substances at different dilutions. First, dilution affects the value of i for electrolytes; the more dilute the solution, the more closely i approaches the limiting value. Thus, we conclude that the extent of ion pairing in electrolyte solutions decreases upon dilution. Second, the lower the charges on the ions, the less i departs from the limiting value because the extent of ion pairing decreases as the ionic charges decrease. Both trends are consistent with simple electrostatics: The force of interaction between charged particles decreases as their separation increases and as their charges decrease.
RELATED EXERCISES: 13.83, 13.84, 13.103, 13.105
TABLE 13.4 • van't Hoff Factors for Several Substances at 25 °C
