CHEMISTRY THE CENTRAL SCIENCE
14 CHEMICAL KINETICS
14.4 THE CHANGE OF CONCENTRATION WITH TIME
The rate laws we have examined so far enable us to calculate the rate of a reaction from the rate constant and reactant concentrations. These rate laws can also be converted into equations that show the relationship between concentrations of reactants or products and time. The mathematics required to accomplish this conversion involves calculus. We do not expect you to be able to perform the calculus operations, but you should be able to use the resulting equations. We will apply this conversion to three of the simplest rate laws: those that are first order overall, those that are second order overall, and those that are zero order overall.
First-Order Reactions
A first-order reaction is one whose rate depends on the concentration of a single reactant raised to the first power. For a reaction of the type A → products, the rate law may be first order:
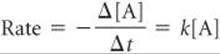
This form of a rate law, which expresses how rate depends on concentration, is called the differential rate law. Using an operation from calculus called integration, this relationship can be transformed into an equation that relates the initial concentration of A, [A]0, to its concentration at any other time t, [A]t:
This form of the rate law is called the integrated rate law. The function “ln” in Equation 14.12 is the natural logarithm (Appendix A.2). Equation 14.12 can also be rearranged to
Equations 14.12 and 14.13 can be used with any concentration units as long as the units are the same for both [A]t and [A]0.
For a first-order reaction, Equation 14.12 or 14.13 can be used in several ways. Given any three of the following quantities, we can solve for the fourth: k, t, [A]0, and [A]t. Thus, you can use these equations to determine (1) the concentration of a reactant remaining at any time after the reaction has started, (2) the time interval required for a given fraction of a sample to react, or (3) the time interval required for a reactant concentration to fall to a certain level.
SAMPLE EXERCISE 14.7 Using the Integrated First-Order Rate Law
The decomposition of a certain insecticide in water at 12 °C follows first-order kinetics with a rate constant of 1.45 yr–1. A quantity of this insecticide is washed into a lake on June 1, leading to a concentration of 5.0 × 10–7 g/cm3. Assume that the average temperature of the lake is 12 °C. (a)What is the concentration of the insecticide on June 1 of the following year? (b) How long will it take for the insecticide concentration to decrease to 3.0 × 10–7 g/cm3?
SOLUTION
Analyze We are given the rate constant for a reaction that obeys first-order kinetics, as well as information about concentrations and times, and asked to calculate how much reactant (insecticide) remains after one year. We must also determine the time interval needed to reach a particular insecticide concentration. Because the exercise gives time in (a) and asks for time in (b), we know that the integrated rate law, Equation 14.13, is required.
Plan
(a) We are given k = 1.45 yr–1, t = 1.00 yr and [insecticide]0 = 5.0 × 10–7 g/cm3, and so Equation 14.13 can be solved for [insecticide]t. (b) We have k = 1.45 yr–1, [insecticide]0 = 5.0 × 10–7 g/cm3, and [insecticide]t = 3.0 × 10–7 g/cm3, and so we can solve Equation 14.13 for time, t.
Solve
(a) Substituting the known quantities into Equation 14.13, we have
ln(3.0 × 10–7) = –(1.45 yr–1)(t) + ln(5.0 × 10–7)
We use the ln function on a calculator to evaluate the second term on the right, giving
ln[insecticide]t = 1 yr = –1.45 + (–14.51) = –15.96
To obtain [insecticide]t = 1 yr, we use the inverse natural logarithm, or ex, function on the calculator:
[insecticide]t = 1 yr = e–15.96 = 1.2 × 10–7 g/cm3
Note that the concentration units for [A]t and [A]0 must be the same.
(b) Again substituting into Equation 14.13, with [insecticide]t = 3.0 × 10–7 g/cm3, gives
t = –[ln(3.0 × 10–7) – ln(5.0 × 10–7)]/1.45 yr–1
= –(–15.02 + 14.51)/1.45 yr–1 = 0.35 yr
Solving for t gives
ln[insecticide]t = 1 yr = –(1.45 yr–1)(1.00 yr) + ln(5.0 × 10–7)
Check In part (a) the concentration remaining after 1.00 yr (that is, 1.2 × 10–7 g/cm3) is less than the original concentration (5.0 × 10–7 g/cm3), as it should be. In (b) the given concentration (3.0 × 10–7 g/cm3) is greater than that remaining after 1.00 yr, indicating that the time must be less than a year. Thus, t = 0.35 yr is a reasonable answer.
PRACTICE EXERCISE
The decomposition of dimethyl ether, (CH3)2O, at 510 °C is a first-order process with a rate constant of 6.8 × 10–4 s–1:
(CH3)2O(g) → CH4(g) + H2(g) + CO(g)
If the initial pressure of (CH3)2O is 135 torr, what is its pressure after 1420 s?
Answer: 51 torr
Equation 14.13 can be used to verify whether a reaction is first order and to determine its rate constant. This equation has the form of the general equation for a straight line, y = mx + b, in which m is the slope and b is the y-intercept of the line (Appendix A.4):
For a first-order reaction, therefore, a graph of ln[A]t versus time gives a straight line with a slope of – k and a y-intercept of ln[A]0. A reaction that is not first order will not yield a straight line.
As an example, consider the conversion of methyl isonitrile (CH3NC) to its isomer acetonitrile (CH3CN) (
FIGURE 14.7). Because experiments show that the reaction is first order, we can write the rate equation:
ln[CH3NC]t = –kt + ln[CH3NC]0
FIGURE 14.7 The first-order reaction of CH3NC conversion into CH3CN.
We run the reaction at a temperature at which methyl isonitrile is a gas (199 °C), and 
FIGURE 14.8 (a) shows how the pressure of this gas varies with time. We can use pressure as a unit of concentration for a gas because we know from the ideal-gas law the pressure is directly proportional to the number of moles per unit volume. Figure 14.8(b) shows that a plot of the natural logarithm of the pressure versus time is a straight line. The slope of this line is –5.1 × 10–5 s–1. (You should verify this for yourself, remembering that your result may vary slightly from ours because of inaccuracies associated with reading the graph.) Because the slope of the line equals –k, the rate constant for this reaction equals 5.1 × 10–5 s–1.
Second-Order Reactions
A second-order reaction is one whose rate depends either on a reactant concentration raised to the second power or on the concentrations of two reactants each raised to the first power. For simplicity, let's consider reactions of the type A → products or A + B → products that are second order in just one reactant, A:
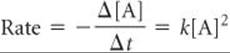
With the use of calculus, this differential rate law can be used to derive the integrated rate law
This equation, like Equation 14.13, has four variables, k, t, [A]0, and[A]t, and any one of these can be calculated knowing the other three. Equation 14.14 also has the form of a straight line (y = mx + b). If the reaction is second order, a plot of 1/[A]t versus t yields a straight line with slope kand y-intercept 1/[A]0. One way to distinguish between first-and second-order rate laws is to graph both ln[A]t and 1/[A]t against t. If the ln[A]t plot is linear, the reaction is first order; if the 1/[A]t plot is linear, the reaction is second order.
GO FIGURE
What can you conclude from the fact that the plot of ln P versus t is linear?
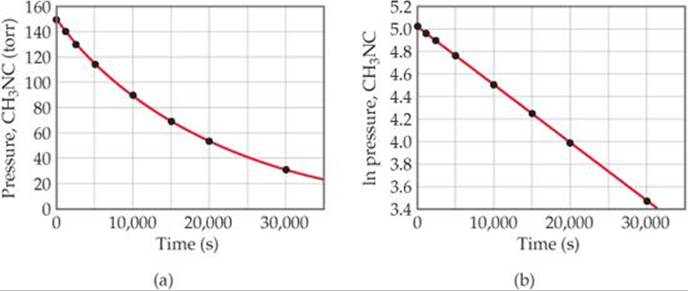
FIGURE 14.8 Kinetic data for conversion of methyl isonitrile into acetonitrile.
SAMPLE EXERCISE 14.8 Determining Reaction Order from the Integrated Rate Law
The following data were obtained for the gas-phase decomposition of nitrogen dioxide at 300 °C, NO2(g) → NO(g) + ½ O2(g):
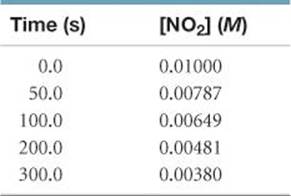
Is the reaction first or second order in NO2?
SOLUTION
Analyze We are given the concentrations of a reactant at various times during a reaction and asked to determine whether the reaction is first or second order.
Plan We can plot ln[NO2] and 1/[NO2] against time. One or the other will be linear, indicating whether the reaction is first or second order.
Solve To graph ln[NO2] and 1/[NO2] against time, we will first prepare the following table from the data given:
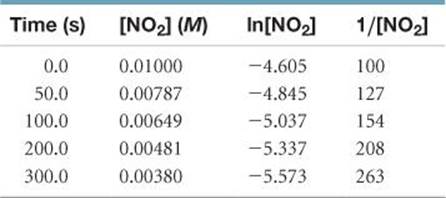
As FIGURE 14.9 shows, only the plot of 1/[NO2] versus time is linear. Thus, the reaction obeys a second-order rate law: Rate = k[NO2]2. From the slope of this straight-line graph, we determine that k = 0.543 M–1 s–1 for the disappearance of NO2.
PRACTICE EXERCISE
The decomposition of NO2 discussed in the Sample Exercise is second order in NO2 with k = 0.543 M–1 s–1. If the initial concentration of NO2 in a closed vessel is 0.0500, what is the concentration of this reactant after 0.500 hr?
Answer: [NO2] = 1.00 × 10–3M
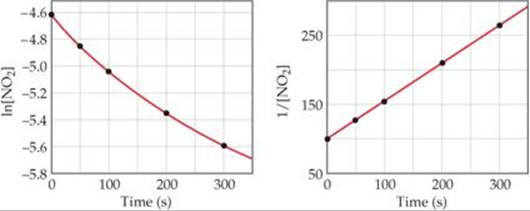
FIGURE 14.9 Kinetic data for decomposition of NO2.
Zero-Order Reactions
We've seen that in a first-order reaction the concentration of a reactant A decreases non-linearly, as shown by the red curve in FIGURE 14.10. As [A] declines, the rate at which it disappears declines in proportion. A zero-order reaction is one in which the rate of disappearance of A isindependent of [A]. The rate law for a zero-order reaction is
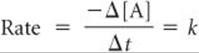
GO FIGURE
At which times during the reaction would you have trouble distinguishing a zero-order reaction from a first-order reaction?
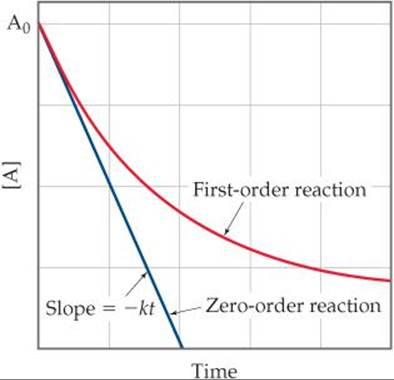
FIGURE 14.10 Comparison of first-order and zero-order reactions for the disappearance of reactant A with time.
The integrated rate law for a zero-order reaction is
[A]t = –kt + [A]0
where [A]t is the concentration of A at time t and [A]0 is the initial concentration. This is the equation for a straight line with vertical intercept [A]0 and slope –kt, as shown in the blue curve in Figure 14.10.
The most common type of zero-order reaction occurs when a gas undergoes decomposition on the surface of a solid. If the surface is completely covered by decomposing molecules, the rate of reaction is constant because the number of reacting surface molecules is constant, so long as there is some gas-phase substance left.
Half-Life
The half-life of a reaction, t1/2, is the time required for the concentration of a reactant to reach half its initial value, [A]t1/2 = ½ [A]0. Half-life is a convenient way to describe how fast a reaction occurs, especially if it is a first-order process. A fast reaction has a short half-life.
We can determine the half-life of a first-order reaction by substituting [A]t½ = ½ [A]0 for [A]t and t1/2 for t in Equation 14.12:
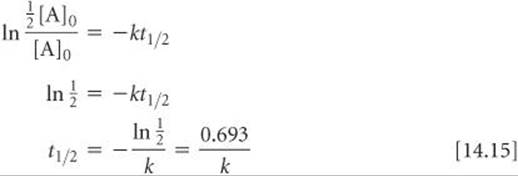
From Equation 14.15, we see that t1/2 for a first-order rate law does not depend on the initial concentration of any reactant. Consequently, the half-life remains constant throughout the reaction. If, for example, the concentration of a reactant is 0.120 M at some instant in the reaction, it will be ½(0.120 M) = 0.060 M after one half-life. After one more half-life passes, the concentration will drop to 0.030 M, and so on. Equation 14.15 also indicates that, for a first-order reaction, we can calculate t1/2 if we know k and calculate k if we know t1/2.
The change in concentration over time for the first-order rearrangement of gaseous methyl isonitrile at 199 °C is graphed in FIGURE 14.11. Because the concentration of this gas is directly proportional to its pressure during the reaction, we have chosen to plot pressure rather than concentration in this graph. The first half-life occurs at 13,600 s (3.78 hr). At a time 13,600 s later, the methyl isonitrile pressure (and therefore, concentration) has decreased to half of one-half, or one-fourth, of the initial value. In a first-order reaction, the concentration of the reactant decreases by one-half in each of a series of regularly spaced time intervals, each interval equal to t1/2.
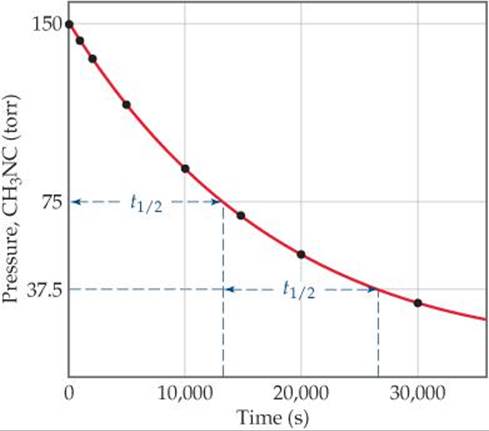
FIGURE 14.11 Kinetic data for the rearrangment of methyl isonitrile to acetonitrile at 199 °C, showing the half-life of the reaction.
GIVE IT SOME THOUGHT
If a solution containing 10.0 g of a substance reacts by first-order kinetics, how many grams remain after 3 half-lives?
CHEMISTRY PUT TO WORK
Methyl Bromide in the Atmosphere
The compounds known as chlorofluorocarbons (CFCs) are well-known agents responsible for the destruction of Earth's protective ozone layer. Another simple molecule that has the potential to destroy the stratospheric ozone layer is methyl bromide, CH3Br (FIGURE 14.12). Because this substance has a wide range of uses, including antifungal treatment of plant seeds, it has been produced in large quantities in the past (about 150 million pounds per year worldwide in 1997, at the height of its production). In the stratosphere, the C — Br bond is broken through absorption of short-wavelength radiation. The resultant Br atoms then catalyze decomposition of O3.
Methyl bromide is removed from the lower atmosphere by a variety of mechanisms, including a slow reaction with ocean water:
To determine the potential importance of CH3Br in destruction of the ozone layer, it is important to know how rapidly the reaction in Equation 14.16 and all other reactions remove CH3Br from the lower atmosphere before it can diffuse into the stratosphere.
The average lifetime of CH3Br in Earth's lower atmosphere is difficult to measure because the conditions that exist in the atmosphere are too complex to be simulated in the laboratory. Instead, scientists analyzed nearly 4000 atmospheric samples collected above the Pacific Ocean for the presence of several trace organic substances, including methyl bromide. From these measurements, it was possible to estimate the atmospheric residence time for CH3Br.
The atmospheric residence time is related to the half-life for CH3Br in the lower atmosphere, assuming the CH3Br decomposes by a first-order process. From the experimental data, the half-life for methyl bromide in the lower atmosphere is estimated to be 0.8 ± 0.1 year. That is, a collection of CH3Br molecules present at any given time will, on average, be 50% decomposed after 0.8 year, 75% decomposed after 1.6 years, and so on. A half-life of 0.8 year, while comparatively short, is still sufficiently long so that CH3Br contributes significantly to the destruction of the ozone layer.
In 1997 an international agreement was reached to phase out use of methyl bromide in developed countries by 2005. However, in recent years exemptions for critical agricultural use have been requested and granted. Nevertheless, worldwide production was down to 25 million pounds in 2009, two-thirds of which is used in the United States.
RELATED EXERCISE: 14.124
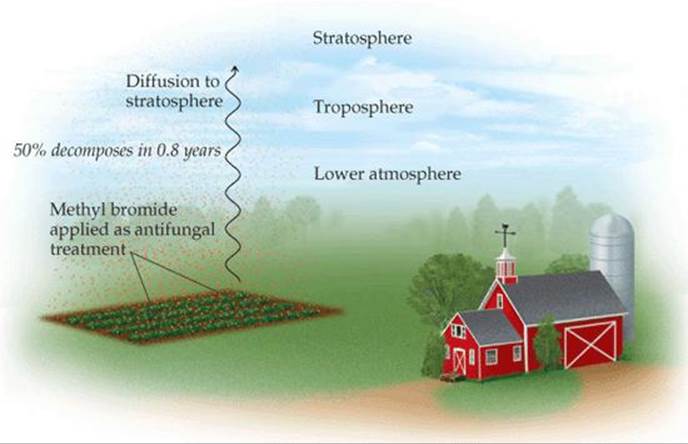
FIGURE 14.12 Distribution and fate of methyl bromide in Earth's atmosphere.
SAMPLE EXERCISE 14.9 Determining the Half-Life of a First-Order Reaction
The reaction of C4H9Cl with water is a first-order reaction. (a) Use Figure 14.4 to estimate the half-life for this reaction. (b) Use the half-life from (a) to calculate the rate constant.
SOLUTION
Analyze We are asked to estimate the half-life of a reaction from a graph of concentration versus time and then to use the half-life to calculate the rate constant for the reaction.
Plan
(a) To estimate a half-life, we can select a concentration and then determine the time required for the concentration to decrease to half of that value. (b) Equation 14.15 is used to calculate the rate constant from the half-life.
Solve
(a) From the graph, we see that the initial value of [C4H9Cl] is 0.100 M. The half-life for this first-order reaction is the time required for [C4H9Cl] to decrease to 0.050 M, which we can read off the graph. This point occurs at approximately 340 s.
(b) Solving Equation 14.15 for k, we have
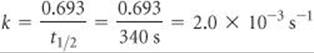
Check At the end of the second half-life, which should occur at 680 s, the concentration should have decreased by yet another factor of 2, to 0.025. Inspection of the graph shows that this is indeed the case.
PRACTICE EXERCISE
(a) Using Equation 14.15, calculate t1/2 for the decomposition of the insecticide described in Sample Exercise 14.7. (b) How long does it take for the concentration of the insecticide to reach one-quarter of the initial value?
Answer: (a) 0.478 yr = 1.51 × 107 s, (b) it takes two half-lives, 2(0.478 yr) = 0.956 yr
The half-life for second-order and other reactions depends on reactant concentrations and therefore changes as the reaction progresses. We obtained Equation 14.15 for the half-life for a first-order reaction by substituting [A]t1/2 = ½ [A]0 for [A]t and t1/2 for t in Equation 14.12. We find the half-life of a second-order reaction by making the same substitutions into Equation 14.14:
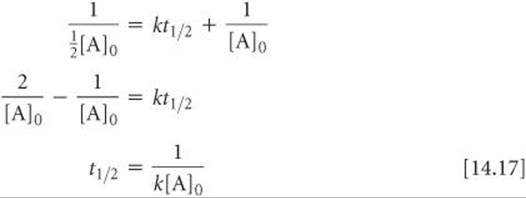
In this case the half-life depends on the initial concentration of reactant—the lower the initial concentration, the longer the half-life.
GIVE IT SOME THOUGHT
How does the half-life of a second-order reaction change as the reaction proceeds?