CHEMISTRY THE CENTRAL SCIENCE
14 CHEMICAL KINETICS
14.6 REACTION MECHANISMS
A balanced equation for a chemical reaction indicates the substances present at the start of the reaction and those present at the end of the reaction. It provides no information, however, about the detailed steps that occur at the molecular level as the reactants are turned into products. The steps by which a reaction occurs is called the reaction mechanism. At the most sophisticated level, a reaction mechanism describes the order in which bonds are broken and formed and the changes in relative positions of the atoms in the course of the reaction.
Elementary Reactions
We have seen that reactions take place because of collisions between reacting molecules. For example, the collisions between molecules of methyl isonitrile (CH3NC) can provide the energy to allow the CH3NC to rearrange to acetonitrile:
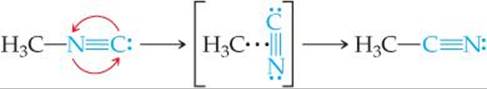
Similarly, the reaction of NO and O3 to form NO2 and O2 appears to occur as a result of a single collision involving suitably oriented and sufficiently energetic NO and O3 molecules:
Both reactions occur in a single event or step and are called elementary reactions.
The number of molecules that participate as reactants in an elementary reaction defines the molecularity of the reaction. If a single molecule is involved, the reaction is unimolecular. The rearrangement of methyl isonitrile is a unimolecular process. Elementary reactions involving the collision of two reactant molecules are bimolecular. The reaction between NO and O3 is bimolecular. Elementary reactions involving the simultaneous collision of three molecules are termolecular. Termolecular reactions are far less probable than unimolecular or bimolecular processes and are rarely encountered. The chance that four or more molecules will collide simultaneously with any regularity is even more remote; consequently, such collisions are never proposed as part of a reaction mechanism.
GIVE IT SOME THOUGHT
What is the molecularity of the elementary reaction?
NO(g) + Cl2(g) → NOCl(g) + Cl(g)
Multistep Mechanisms
The net change represented by a balanced chemical equation often occurs by a multistep mechanism consisting of a sequence of elementary reactions. For example, below 225 °C, the reaction
appears to proceed in two elementary reactions (or two elementary steps), each of which is bimolecular. First, two NO2 molecules collide, and an oxygen atom is transferred from one to the other. The resultant NO3 then collides with a CO molecule and transfers an oxygen atom to it:
NO2(g) + NO2(g) → NO3(g) + NO(g)
NO3(g) + CO(g) → NO2(g) + CO2(g)
Thus, we say that the reaction occurs by a two-step mechanism.
The chemical equations for the elementary reactions in a multistep mechanism must always add to give the chemical equation of the overall process. In the present example the sum of the two elementary reactions is
2 NO2(g) + NO3(g) + CO(g) → NO2(g) + NO3(g) + NO(g) + CO2(g)
Simplifying this equation by eliminating substances that appear on both sides gives Equation 14.23, the net equation for the process.
Because NO3 is neither a reactant nor a product of the reaction—it is formed in one elementary reaction and consumed in the next—it is called an intermediate. Multistep mechanisms involve one or more intermediates. Intermediates are not the same as transition states, as shown in 
FIGURE 14.20. Intermediates can be stable and can therefore sometimes be identified and even isolated. Transition states, on the other hand, are always inherently unstable and as such can never be isolated. Nevertheless, the use of advanced “ultrafast” techniques sometimes allows us to characterize them.
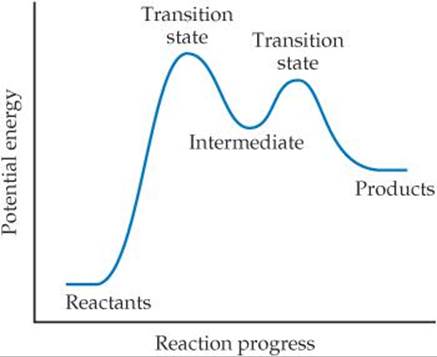
FIGURE 14.20 The energy profile of a reaction, showing transition states and an intermediate.
SAMPLE EXERCISE 14.12 Determining Molecularity and Identifying Intermediates
It has been proposed that the conversion of ozone into O2 proceeds by a two-step mechanism:
O3(g) → O2(g) + O(g)
O3(g) + O(g) → 2 O2(g)
(a) Describe the molecularity of each elementary reaction in this mechanism.
(b) Write the equation for the overall reaction. (c) Identify the intermediate(s).
SOLUTION
Analyze We are given a two-step mechanism and asked for (a) the molecularities of each of the two elementary reactions, (b) the equation for the overall process, and (c) the intermediate.
Plan The molecularity of each elementary reaction depends on the number of reactant molecules in the equation for that reaction. The overall equation is the sum of the equations for the elementary reactions. The intermediate is a substance formed in one step of the mechanism and used in another and therefore not part of the equation for the overall reaction.
Solve
(a) The first elementary reaction involves a single reactant and is consequently unimolecular. The second reaction, which involves two reactant molecules, is bimolecular.
(b) Adding the two elementary reactions gives
2 O3(g) + O(g) → 3 O2(g) + O(g)
Because O(g) appears in equal amounts on both sides of the equation, it can be eliminated to give the net equation for the chemical process:
2 O3(g) → 3 O2(g)
(c) The intermediate is O(g). It is neither an original reactant nor a final product but is formed in the first step of the mechanism and consumed in the second.
PRACTICE EXERCISE
For the reaction
Mo(CO)6 + P(CH3)3 → Mo(CO)5 P(CH3)3 + CO
the proposed mechanism is
Mo(CO)6 → Mo(CO)5 + CO
Mo(CO)5 + P(CH3)3 → Mo(CO)5 P(CH3)3
(a) Is the proposed mechanism consistent with the equation for the overall reaction? (b) What is the molecularity of each step of the mechanism? (c) Identify the intermediate(s).
Answer: (a) Yes, the two equations add to yield the equation for the reaction. (b) The first elementary reaction is unimolecular, and the second one is bimolecular. (c) Mo(CO)5
Rate Laws for Elementary Reactions
In Section 14.3 we stressed that rate laws must be determined experimentally; they cannot be predicted from the coefficients of balanced chemical equations. We are now in a position to understand why this is so. Every reaction is made up of a series of one or more elementary steps, and the rate laws and relative speeds of these steps dictate the overall rate law for the reaction. Indeed, the rate law for a reaction can be determined from its mechanism, as we will see shortly, and compared with the experimental rate law. Thus, our next challenge in kinetics is to arrive at reaction mechanisms that lead to rate laws consistent with those observed experimentally. We start by examining the rate laws of elementary reactions.
Elementary reactions are significant in a very important way: If a reaction is elementary, its rate law is based directly on its molecularity. For example, consider the unimolecular reaction
A → products
As the number of A molecules increases, the number that react in a given time interval increases proportionally. Thus, the rate of a unimolecular process is first order:
Rate = k[A]
For bimolecular elementary steps, the rate law is second order, as in the reaction
A + B → products Rate = k[A][B]
The second-order rate law follows directly from collision theory. If we double the concentration of A, the number of collisions between molecules of A and B doubles; likewise, if we double [B], the number of collisions between A and B doubles. Therefore, the rate law is first order in both [A] and [B] and second order overall.
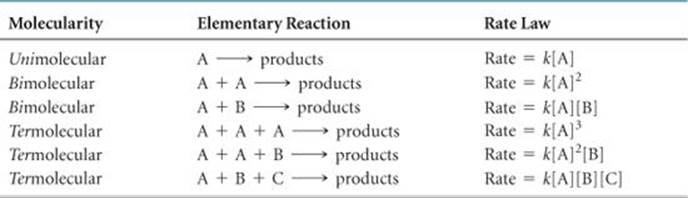
The rate laws for all feasible elementary reactions are given in 
TABLE 14.3. Notice how each rate law follows directly from the molecularity of the reaction. It is important to remember, however, that we cannot tell by merely looking at a balanced, overall chemical equation whether the reaction involves one or several elementary steps.
TABLE 14.3 • Elementary Reactions and Their Rate Laws
SAMPLE EXERCISE 14.13 Predicting the Rate Law for an Elementary Reaction
If the following reaction occurs in a single elementary reaction, predict its rate law:
H2(g) + Br2(g) → 2 HBr(g)
SOLUTION
Analyze We are given the equation and asked for its rate law, assuming that it is an elementary process.
Plan Because we are assuming that the reaction occurs as a single elementary reaction, we are able to write the rate law using the coefficients for the reactants in the equation as the reaction orders.
Solve The reaction is bimolecular, involving one molecule of H2 and one molecule of Br2. Thus, the rate law is first order in each reactant and second order overall:
Rate = k[H2][Br2]
Comment Experimental studies of this reaction show that the reaction actually has a very different rate law:
Rate = k[H2][Br2]1/2
Because the experimental rate law differs from the one obtained by assuming a single elementary reaction, we can conclude that the mechanism cannot occur by a single elementary step. It must, therefore, involve two or more elementary steps.
PRACTICE EXERCISE
Consider the following reaction: 2 NO(g) + Br2(g) → 2 NOBr(g). (a) Write the rate law for the reaction, assuming it involves a single elementary reaction. (b) Is a single-step mechanism likely for this reaction?
Answer: (a) Rate = k[NO]2 [Br2], (b) No, because termolecular reactions are very rare.
The Rate-Determining Step for a Multistep Mechanism
As with the reaction in Sample Exercise 14.13, most reactions occur by mechanisms that involve two or more elementary reactions. Each step of the mechanism has its own rate constant and activation energy. Often one step is much slower than the others, and the overall rate of a reaction cannot exceed the rate of the slowest elementary step. Because the slow step limits the overall reaction rate, it is called the rate-determining step (or rate-limiting step).
To understand the concept of the rate-determining step for a reaction, consider a toll road with two toll plazas (
FIGURE 14.21). Cars enter the toll road at point 1 and pass through toll plaza A. They then pass an intermediate point 2 before passing through toll plaza B and arriving at point 3. We can envision this trip along the toll road as occurring in two elementary steps:
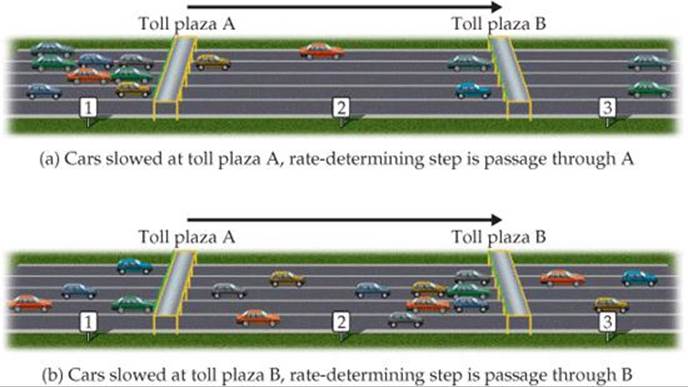
FIGURE 14.21 Rate-determining steps in traffic flow on a toll road.
Now suppose that one or more gates at toll plaza A are malfunctioning, so that traffic backs up behind the gates, as depicted in Figure 14.21(a). The rate at which cars can get to point 3 is limited by the rate at which they can get through the traffic jam at plaza A. Thus, step 1 is the rate-determining step of the journey along the toll road. If, however, all gates at A are functioning but one or more at B are not, traffic flows quickly through A but gets backed up at B, as depicted in Figure 14.21(b). In this case step 2 is the rate-determining step.
In the same way, the slowest step in a multistep reaction limits the overall rate. By analogy to Figure 14.21(a), the rate of a fast step following the rate-determining step does not speed up the overall rate. If the slow step is not the first one, as is the case in Figure 14.21(b), the faster preceding steps produce intermediate products that accumulate before being consumed in the slow step. In either case, the rate-determining step governs the rate law for the overall reaction.
GIVE IT SOME THOUGHT
Why can't the rate law for a reaction generally be deduced from the balanced equation for the reaction?
Mechanisms with a Slow Initial Step
We can most easily see the relationship between the slow step in a mechanism and the rate law for the overall reaction by considering an example in which the first step in a multistep mechanism is the rate-determining step. Consider the reaction of NO2 and CO to produce NO and CO2(Equation 14.23). Below 225 °C, it is found experimentally that the rate law for this reaction is second order in NO2 and zero order in CO: Rate = k[NO2]2. Can we propose a reaction mechanism consistent with this rate law? Consider the two-step mechanism:*
Step 2 is much faster than step 1; that is, k2 >> k1, telling us that the intermediate NO3(g) is slowly produced in step 1 and immediately consumed in step 2.
Because step 1 is slow and step 2 is fast, step 1 is the rate-determining step. Thus, the rate of the overall reaction depends on the rate of step 1, and the rate law of the overall reaction equals the rate law of step 1. Step 1 is a bimolecular process that has the rate law
Rate = k1[NO2]2
Thus, the rate law predicted by this mechanism agrees with the one observed experimentally. The reactant CO is absent from the rate law because it reacts in a step that follows the rate-determining step.
A scientist would not, at this point, say that we have “proved” that this mechanism is correct. All we can say is that the rate law predicted by the mechanism is consistent with experiment. There could easily be a different sequence of steps that leads to the same rate law. If, however, the predicted rate law of the proposed mechanism disagrees with experiment, we know for certain that the mechanism cannot be correct.
SAMPLE EXERCISE 14.14 Determining the Rate Law for a Multistep Mechanism
The decomposition of nitrous oxide, N2O, is believed to occur by a two-step mechanism:
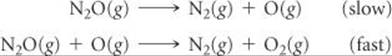
(a) Write the equation for the overall reaction. (b) Write the rate law for the overall reaction.
SOLUTION
Analyze Given a multistep mechanism with the relative speeds of the steps, we are asked to write the overall reaction and the rate law for that overall reaction.
Plan (a) Find the overall reaction by adding the elementary steps and eliminating the intermediates. (b) The rate law for the overall reaction will be that of the slow, rate-determining step.
Solve (a) Adding the two elementary reactions gives
2 N2O(g) + O(g) → 2 N2(g) + 2 O2(g) + O(g)
Omitting the intermediate, O(g), which occurs on both sides of the equation, gives the overall reaction:
2 N2O(g) → 2 N2(g) + O2(g)
(b) The rate law for the overall reaction is just the rate law for the slow, rate-determining elementary reaction. Because that slow step is a unimolecular elementary reaction, the rate law is first order:
Rate = k[N2O]
PRACTICE EXERCISE
Ozone reacts with nitrogen dioxide to produce dinitrogen pentoxide and oxygen:
O3(g) + 2 NO2(g) → N2O5(g) + O2(g)
The reaction is believed to occur in two steps:
The experimental rate law is rate = k[O3][NO2]. What can you say about the relative rates of the two steps of the mechanism?
Answer: Because the rate law conforms to the molecularity of the first step, that must be the rate-determining step. The second step must be much faster than the first one.
Mechanisms with a Fast Initial Step
It is less straightforward to derive the rate law for a mechanism in which an intermediate is a reactant in the rate-determining step. This situation arises in multistep mechanisms when the first step is fast and therefore not the rate-determining step. Let's consider one example: the gas-phase reaction of nitric oxide (NO) with bromine (Br2):
The experimentally determined rate law for this reaction is second order in NO and first order in Br2:
We seek a reaction mechanism that is consistent with this rate law. One possibility is that the reaction occurs in a single termolecular step:
As noted in Practice Exercise 14.13, this does not seem likely because termolecular processes are so rare.
GIVE IT SOME THOUGHT
Why are termolecular elementary steps rare in gas-phase reactions?
Let's consider an alternative mechanism that does not involve a termolecular step:
In this mechanism, step 1 involves two processes: a forward reaction and its reverse.
Because step 2 is the rate-determining step, the rate law for that step governs the rate of the overall reaction:
However, NOBr2 is an intermediate generated in the forward reaction of step 1. Intermediates are usually unstable and have a low, unknown concentration. Thus, the rate law of Equation 14.28 depends on the unknown concentration of an intermediate. This is not desirable. Instead, in general, we want to express the rate law for any reaction in terms of the reactants, or the products if necessary, of the reaction.
With the aid of some assumptions, we can express the concentration of the intermediate NOBr2 in terms of the concentrations of the starting reactants NO and Br2. We first assume that NOBr2 is unstable and does not accumulate to any significant extent in the reaction mixture. Once formed, NOBr2 can be consumed either by reacting with NO to form NOBr or by re-forming NO and Br2. The first of these possibilities is step 2 of our alternative mechanism, a slow process. The second is the reverse of step 1, a unimolecular process:
Because step 2 is slow, we assume that most of the NOBr2 falls apart according to this reaction. Thus, we have both the forward and reverse reactions of step 1 occurring much faster than step 2. Because they occur rapidly relative to step 2, the forward and reverse reactions of step 1 establish an equilibrium. As in any other dynamic equilibrium, the rate of the forward reaction equals that of the reverse reaction:
Solving for [NOBr2], we have
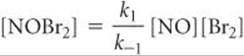
Substituting this relationship into Equation 14.28, we have
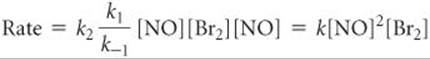
where the experimental rate constant k equals k2k1/k–1. This expression is consistent with the experimental rate law (Equation 14.25). Thus, our alternative mechanism (Equation 14.27), which involves two steps but only unimolecular and bimolecular processes, is far more probable than the single-step termolecular mechanism of Equation 14.26.
In general, whenever a fast step precedes a slow one, we can solve for the concentration of an intermediate by assuming that an equilibrium is established in the fast step.
SAMPLE EXERCISE 14.15 Deriving the Rate Law for a Mechanism with a Fast Initial Step
Show that the following mechanism for Equation 14.24 also produces a rate law consistent with the experimentally observed one:
SOLUTION
Analyze We are given a mechanism with a fast initial step and asked to write the rate law for the overall reaction.
Plan The rate law of the slow elementary step in a mechanism determines the rate law for the overall reaction. Thus, we first write the rate law based on the molecularity of the slow step. In this case the slow step involves the intermediate N2O2 as a reactant. Experimental rate laws, however, do not contain the concentrations of intermediates; instead they are expressed in terms of the concentrations of starting substances. Thus, we must relate the concentration of N2O2 to the concentration of NO by assuming that an equilibrium is established in the first step.
Solve The second step is rate determining, so the overall rate is
Rate = k2[N2O2][Br2]
We solve for the concentration of the intermediate N2O2 by assuming that an equilibrium is established in step 1; thus, the rates of the forward and reverse reactions in step 1 are equal:
k1[NO]2 = k–1[N2O2]
Solving for the concentration of the intermediate, N2O2, gives
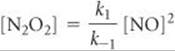
Substituting this expression into the rate expression gives
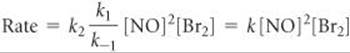
Thus, this mechanism also yields a rate law consistent with the experimental one.
PRACTICE EXERCISE
The first step of a mechanism involving the reaction of bromine is
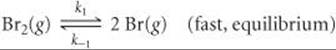
What is the expression relating the concentration of Br(g) to that of Br2(g)?
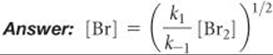
So far we have considered only three reaction mechanisms: one for a reaction that occurs in a single elementary step and two for simple multistep reactions where there is one rate-determining step. There are other more complex mechanisms, however. If you take a biochemistry class, for example, you will learn about cases in which you have to assume that the concentration of an intermediate cannot be neglected in deriving the rate law. Furthermore, some mechanisms require a large number of steps, sometimes 35 or more, to arrive at a rate law that agrees with experimental data!