CHEMISTRY THE CENTRAL SCIENCE

14 CHEMICAL KINETICS

EXERCISES

VISUALIZING CONCEPTS

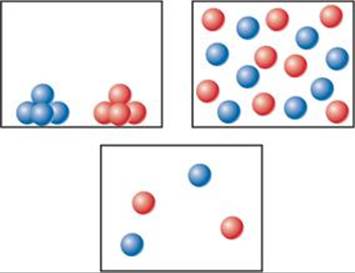
14.1 For which one of the following vessels for the reaction A + B → C is the reaction the fastest? Assume all vessels are at the same temperature. [Section 4.1]

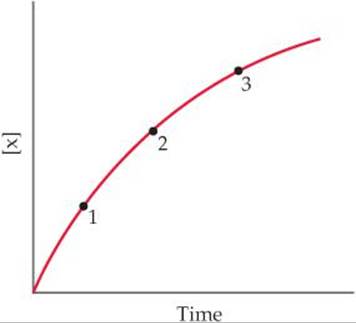
14.2 Consider the following graph of the concentration of a substance over time. (a) Is X a reactant or product of the reaction? (b) Is the reaction speeding up, slowing down, or not changing its rate as time progresses? (c) Why is the average rate of the reaction different between points 1 and 2 than between points 2 and 3? [Section 14.2]

14.3 You study the rate of a reaction, measuring both the concentration of the reactant and the concentration of the product as a function of time, and obtain the following results:

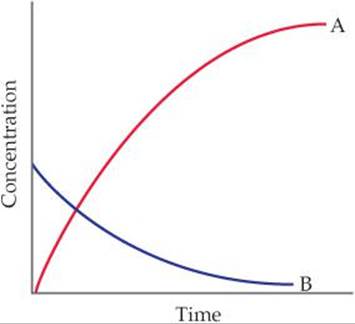
Which chemical equation is consistent with these data: (a) A → B, (b) B → A, (c) A → 2 B, (d) B → 2 A? Explain your choice. [Section 14.2]

14.4 You perform the reaction K + L → M, monitor the production of M over time, and then plot this graph from your data:

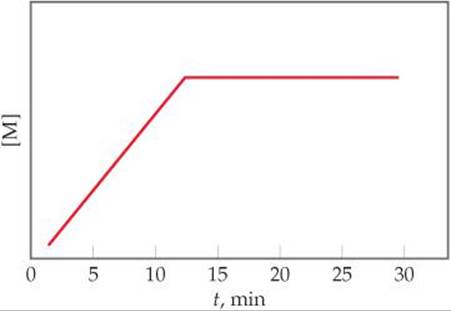
(a) Is the reaction occurring at a constant rate from t = 0 to t = 15 min? Explain. (b) Is the reaction completed at t = 15 min? Explain.

14.5 You perform a series of experiments for the reaction A → B + C and find that the rate law has the form rate = k[A]^x. Determine the value of x in each of the following cases: (a) There is no rate change when [A]₀ is tripled. (b) The rate increases by a factor of 9 when [A]₀ is tripled.(c) When [A]₀ is doubled, the rate increases by a factor of 8. [Section 14.3]

14.6 The following diagrams represent mixtures of NO(g) and O₂(g). These two substances react as follows:

2 NO(g) + O₂(g) → 2 NO₂(g)

It has been determined experimentally that the rate is second order in NO and first order in O₂. Based on this fact, which of the following mixtures will have the fastest initial rate? [Section 14.3]

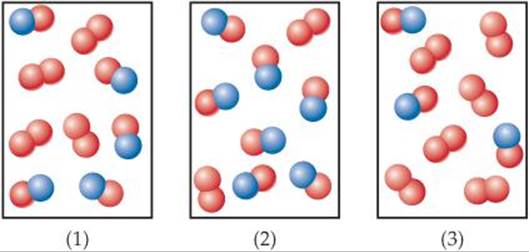
14.7 A friend studies a first-order reaction and obtains the following three graphs for experiments done at two different temperatures. (a) Which two graphs represent experiments done at the same temperature? What accounts for the difference in these two graphs? In what way are they the same? (b) Which two graphs represent experiments done with the same starting concentration but at different temperatures? Which graph probably represents the lower temperature? How do you know? [Section 14.4]

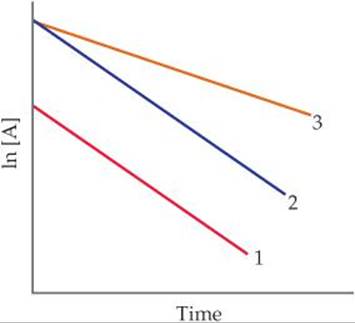
14.8 (a) Given the following diagrams at t = 0 min and t = 30 min, what is the half-life of the reaction if it follows first-order kinetics?

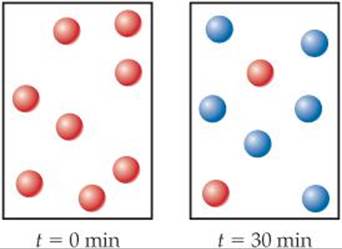
(b) After four half-life periods for a first-order reaction, what fraction of reactant remains? [Section 14.4]

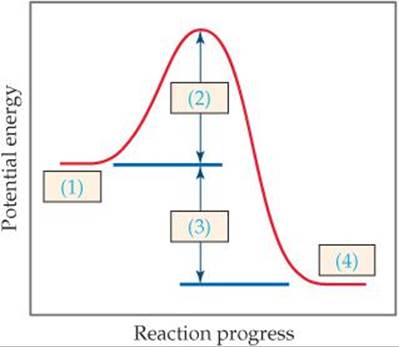
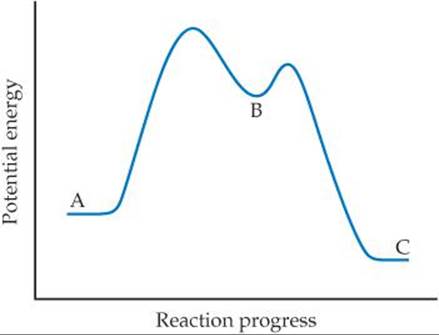
14.9 The following diagram shows the reaction profile of a reaction. Label the components indicated by the boxes. [Section 14.5]

14.10 You study the effect of temperature on the rate of two reactions and graph the natural logarithm of the rate constant for each reaction as a function of 1/T. How do the two graphs compare (a) if the activation energy of the second reaction is higher than the activation energy of the first reaction but the two reactions have the same frequency factor, and (b) if the frequency factor of the second reaction is higher than the frequency factor of the first reaction but the two reactions have the same activation energy? [Section 14.5]

14.11 The following graph shows two different reaction pathways for the same overall reaction at the same temperature. (a) Which pathway is slower? Why? (b) How can there be two different reaction pathways for the same reaction at the same temperature? Discuss. [Section 14.6]

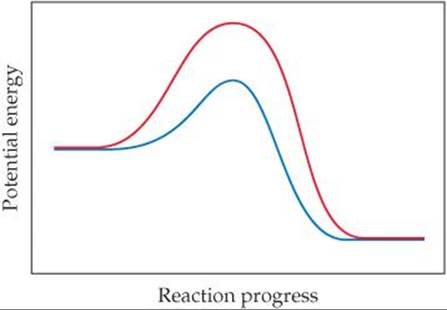
14.12 Consider the diagram that follows, which represents two steps in an overall reaction. The red spheres are oxygen, the blue ones nitrogen, and the green ones fluorine. (a) Write the chemical equation for each step in the reaction. (b) Write the equation for the overall reaction. (c)Identify the intermediate in the mechanism. (d) Write the rate law for the overall reaction if the first step is the slow, rate-determining step. [Section 14.6]

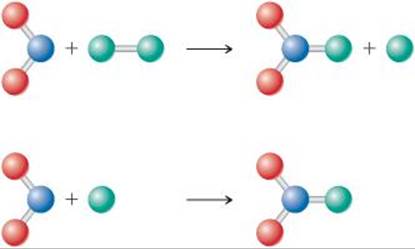
14.13 Based on the following reaction profile, how many intermediates are formed in the reaction A → C? How many transition states are there? Which step is the fastest? Is the reaction A → C exothermic or endothermic? [Section 14.6]

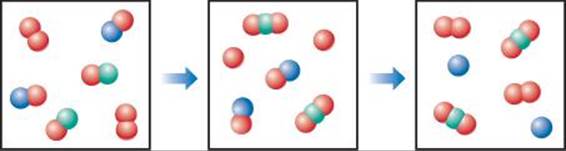
14.14 Draw a possible transition state for the bimolecular reaction depicted here. (The blue spheres are nitrogen atoms, and the red ones are oxygen atoms.) Use dashed lines to represent the bonds that are in the process of being broken or made in the transition state. [Section 14.6]

14.15 The following diagram represents an imaginary two-step mechanism. Let the red spheres represent element A, the green ones element B, and the blue ones element C. (a) Write the equation for the net reaction that is occurring. (b) Identify the intermediate. (c) Identify the catalyst. [Sections 14.6 and 14.7]

14.16 Draw a graph showing the reaction pathway for an overall exothermic reaction with two intermediates that are produced at different rates. On your graph indicate the reactants, products, intermediates, transition states, and activation energies. [Sections 14.6 and 14.7]

REACTION RATES (sections 14.1 and 14.2)

14.17 (a) What is meant by the term reaction rate? (b) Name three factors that can affect the rate of a chemical reaction. (c) Is the rate of disappearance of reactants always the same as the rate of appearance of products? Explain.

14.18 (a) What are the units usually used to express the rates of reactions occurring in solution? (b) From your everyday experience, give two examples of the effects of temperature on the rates of reactions. (c) What is the difference between average rate and instantaneous rate?

______

14.19 Consider the following hypothetical aqueous reaction: A(aq) → B(aq). A flask is charged with 0.065 mol of A in a total volume of 100.0 mL. The following data are collected:

(a) Calculate the number of moles of B at each time in the table, assuming that there are no molecules of B at time zero, and that A cleanly converts to B with no intermediates. (b) Calculate the average rate of disappearance of A for each 10-min interval in units of M/s. (c) Between t= 10 min and t = 30 min, what is the average rate of appearance of B in units of M/s? Assume that the volume of the solution is constant.

14.20 A flask is charged with 0.100 mol of A and allowed to react to form B according to the hypothetical gas-phase reaction A(g) → B(g). The following data are collected:

(a) Calculate the number of moles of B at each time in the table, assuming that A is cleanly converted to B with no intermediates. (b) Calculate the average rate of disappearance of A for each 40-s interval in units of mol/s. (c) What additional information would be needed to calculate the rate in units of concentration per time?

______

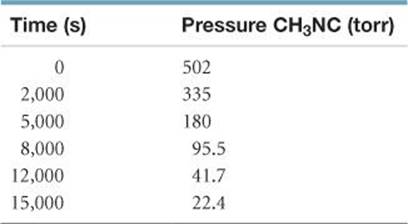
14.21 The isomerization of methyl isonitrile (CH₃NC) to acetonitrile (CH₃CN) was studied in the gas phase at 215 °C, and the following data were obtained:

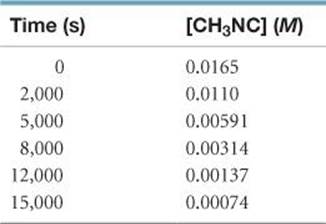
(a) Calculate the average rate of reaction, in M/s, for the time interval between each measurement. (b) Calculate the average rate of reaction over the entire time of the data from t = 0 to t = 15,000s. (c) Graph [CH₃NC] versus time and determine the instantaneous rates in M/s at t = 5000 s and t = 8000 s.

14.22 The rate of disappearance of HCl was measured for the following reaction:

CH₃OH(aq) + HCl(aq) → CH₃Cl(aq) + H₂O(l)

The following data were collected:

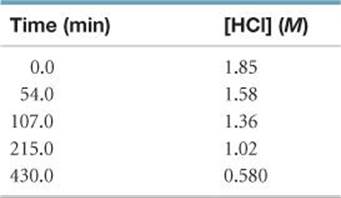
(a) Calculate the average rate of reaction, in M/s, for the time interval between each measurement. (b) Calculate the average rate of reaction for the entire time for the data from t = 0.0 min to t = 430.0 min.

(c) Graph [HCl] versus time and determine the instantaneous rates in M/min and M/s at t = 75.0 min and t = 250 min.

______

14.23 For each of the following gas-phase reactions, indicate how the rate of disappearance of each reactant is related to the rate of appearance of each product:

(a) H₂O₂(g) → H₂(g) + O₂(g)

(b) 2 N₂O(g) → 2 N₂(g) + O₂(g)

(c) N₂(g) + 3 H₂(g) → 2 NH₃(g)

(d) C₂H₅NH₂(g) → C₂H₄(g) + NH₃(g)

14.24 For each of the following gas-phase reactions, write the rate expression in terms of the appearance of each product and disappearance of each reactant:

(a) 2 H₂O(g) → 2 H₂(g) + O₂(g)

(b) 2 SO₂(g) + O₂(g) → 2 SO₃(g)

(c) 2 NO(g) + 2 H₂(g) → N₂(g) + 2 H₂O(g)

(d) N₂(g) + 2 H₂(g) → N₂H₄(g)

______

14.25 (a) Consider the combustion of H₂(g): 2 H₂(g) + O₂(g) → 2 H₂O(g). If hydrogen is burning at the rate of 0.48 mol/s, what is the rate of consumption of oxygen? What is the rate of formation of water vapor? (b) The reaction 2 NO(g) + Cl₂(g) → 2 NOCl(g) is carried out in a closed vessel. If the partial pressure of NO is decreasing at the rate of 56 torr/min, what is the rate of change of the total pressure of the vessel?

14.26 (a) Consider the combustion of ethylene, C₂H₄(g) + 3 O₂(g) → 2 CO₂(g) + 2 H₂O(g). If the concentration of C₂H₄ is decreasing at the rate of 0.036 M/s, what are the rates of change in the concentrations of CO₂ and H₂O? (b) The rate of decrease in N₂H₄ partial pressure in a closed reaction vessel from the reaction N₂H₄(g) + H₂(g) → 2 NH₃(g) is 74 torr per hour. What are the rates of change of NH₃ partial pressure and total pressure in the vessel?

RATE LAWS (section 14.3)

14.27 A reaction A + B → C obeys the following rate law: Rate = k [B]². (a) If [A] is doubled, how will the rate change? Will the rate constant change? Explain. (b) What are the reaction orders for A and B? What is the overall reaction order? (c) What are the units of the rate constant?

14.28 Consider a hypothetical reaction between A, B, and C that is first order in A, zero order in B, and second order in C. (a) Write the rate law for the reaction. (b) How does the rate change when [A] is doubled and the other reactant concentrations are held constant? (c) How does the rate change when [B] is tripled and the other reactant concentrations are held constant? (d) How does the rate change when [C] is tripled and the other reactant concentrations are held constant? (e) By what factor does the rate change when the concentrations of all three reactants are tripled? (f) By what factor does the rate change when the concentrations of all three reactants are cut in half?

______

14.29 The decomposition reaction of N₂O₅ in carbon tetrachloride is 2 N₂O₅ → 4 NO₂ + O₂. The rate law is first order in N₂O₅. At 64 °C the rate constant is 4.82 × 10^–3 s^–1. (a) Write the rate law for the reaction. (b) What is the rate of reaction when [N₂O₅] = 0.0240 M? (c) What happens to the rate when the concentration of N₂O₅ is doubled to 0.0480 M? (d) What happens to the rate when the concentration of N₂O₅ is halved to 0.0120 M?

14.30 Consider the following reaction:

2 NO(g) + 2 H₂(g) → N₂(g) + 2 H₂O(g)

(a) The rate law for this reaction is first order in H₂ and second order in NO. Write the rate law. (b) If the rate constant for this reaction at 1000 K is 6.0 × 10⁴M^–2 s^–1, what is the reaction rate when [NO] = 0.035 M and [H₂] = 0.015 M? (c) What is the reaction rate at 1000 K when the concentration of NO is increased to 0.10 M, while the concentration of H₂ is 0.010 M? (d) What is the reaction rate at 1000 K if [NO] is decreased to 0.010 M and [H₂] is increased to 0.030 M?

______

14.31 Consider the following reaction:

CH₃Br(aq) + OH^–(aq) → CH₃OH(aq) + Br^–(aq)

The rate law for this reaction is first order in CH₃Br and first order in OH^–. When [CH₃Br] is 5.0 × 10^–3M and [OH^–] is 0.050 M, the reaction rate at 298 K is 0.0432 M/s. (a) What is the value of the rate constant? (b) What are the units of the rate constant? (c) What would happen to the rate if the concentration of OH^– were tripled? (d) What would happen to the rate if the concentration of both reactants were tripled?

14.32 The reaction between ethyl bromide (C₂H₅Br) and hydroxide ion in ethyl alcohol at 330 K, C₂H₅Br(alc) + OH^–(alc) → C₂H₅OH(l) + Br^–(alc), is first order each in ethyl bromide and hydroxide ion. When [C₂H₅Br] is 0.0477 M and [OH^–] is 0.100 M, the rate of disappearance of ethyl bromide is 1.7 × 10^–7M/s. (a) What is the value of the rate constant? (b) What are the units of the rate constant? (c) How would the rate of disappearance of ethyl bromide change if the solution were diluted by adding an equal volume of pure ethyl alcohol to the solution?

______

14.33 The iodide ion reacts with hypochlorite ion (the active ingredient in chlorine bleaches) in the following way: OCl^– + I^– → OI^– + Cl^–. This rapid reaction gives the following rate data:

(a) Write the rate law for this reaction. (b) Calculate the rate constant with proper units. (c) Calculate the rate when [OCl^–] = 2.0 × 10^–3M and [I^–] = 5.0 × 10^–4M.

14.34 The reaction 2 ClO₂(aq) + 2 OH^–(aq) → ClO₃^–(aq) + ClO₂^–(aq) + H₂O(l) was studied with the following results:

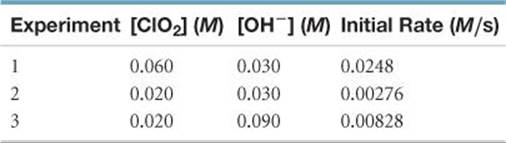
(a) Determine the rate law for the reaction. (b) Calculate the rate constant with proper units. (c) Calculate the rate when [ClO₂] = 0.100 M and [OH^–] = 0.050 M.

______

14.35 The following data were measured for the reaction BF₃(g) + NH₃(g) → F₃BNH₃(g):

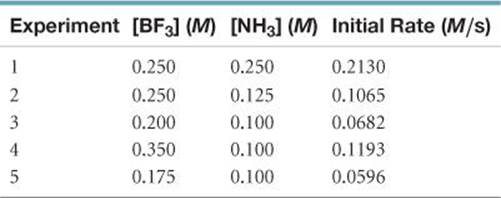
(a) What is the rate law for the reaction? (b) What is the over all order of the reaction? (c) Calculate the rate constant with proper units? (d) What is the rate when [BF₃] = 0.100 M and [NH₃] = 0.500 M?

14.36 The following data were collected for the rate of disappearance of NO in the reaction 2 NO(g) + O₂(g) → 2 NO₂(g):

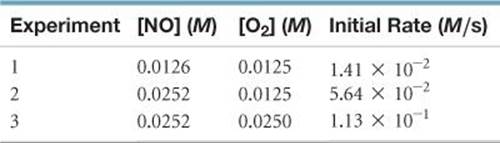
(a) What is the rate law for the reaction? (b) What are the units of the rate constant? (c) What is the average value of the rate constant calculated from the three data sets? (d) What is the rate of disappearance of NO when [NO] = 0.0750 M and [O₂] = 0.0100 M? (e) What is the rate of disappearance of O₂ at the concentrations given in part (d)?

______

[14.37] Consider the gas-phase reaction between nitric oxide and bromine at 273 °C: 2 NO(g) + Br₂(g) → 2 NOBr(g). The following data for the initial rate of appearance of NOBr were obtained:

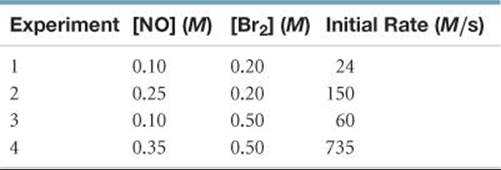
(a) Determine the rate law. (b) Calculate the average value of the rate constant for the appearance of NOBr from the four data sets. (c) How is the rate of appearance of NOBr related to the rate of disappearance of Br₂? (d) What is the rate of disappearance of Br₂ when [NO] = 0.075M and [Br₂] = 0.25 M?

[14.38] Consider the reaction of peroxydisulfate ion (S₂O₈^2–) with iodide ion (I^–) in aqueous solution:

S₂O₈^2– (aq) + 3 I^–(aq) → 2 SO₄^2–(aq) + I₃^–(aq)

At a particular temperature the initial rate of disappearance of S₂O₈^2– varies with reactant concentrations in the following manner:

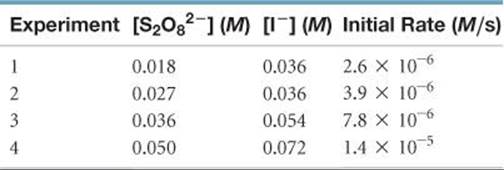
(a) Determine the rate law for the reaction and state the units of the rate constant. (b) What is the average value of the rate constant for the disappearance of S₂O₈^2– based on the four sets of data? (c) How is the rate of disappearance of S₂O₈^2–related to the rate of disappearance of I^–?(d) What is the rate of disappearance of I^– when [S₂O₈^2–] = 0.025 M and [I^–] = 0.050 M?

CHANGE OF CONCENTRATION WITH TIME (section 14.4)

14.39 (a) Define the following symbols that are encountered in rate equations for the generic reaction A → B: [A]₀, t_1/2 [A]_t, k. (b) What quantity, when graphed versus time, will yield a straight line for a first-order reaction? (c) How can you calculate the rate constant for a first-order reaction from the graph you made in part (b)?

14.40 (a) For a generic second-order reaction A → B, what quantity, when graphed versus time, will yield a straight line? (b) What is the slope of the straight line from part (a)? (c) How do the half-lives of first-order and second-order reactions differ?

______

14.41 For the generic reaction A → B that is zero order in A, what would you graph in order to obtain the rate constant?

14.42 Sketch a graph for the generic first-order reaction A → B that has concentration of A on the vertical axis and time on the horizontal axis. (a) Is this graph linear? Explain. (b) Indicate on your graph the half-life for the reaction.

______

14.43 (a) The gas-phase decomposition of SO₂Cl₂, SO₂Cl₂(g) → SO₂(g) + Cl₂(g), is first order in SO₂Cl₂. At 600 K the half-life for this process is 2.3 × 10⁵ s. What is the rate constant at this temperature? (b) At 320 °C the rate constant is 2.2 × 10^–5 s^–1. What is the half-life at this temperature?

14.44 Molecular iodine, I₂(g), dissociates into iodine atoms at 625 K with a first-order rate constant of 0.271 s^–1. (a) What is the half-life for this reaction? (b) If you start with 0.050 M I₂ at this temperature, how much will remain after 5.12 s assuming that the iodine atoms do not recombine to form I₂?

______

14.45 As described in Exercise 14.43, the decomposition of sulfuryl chloride (SO₂Cl₂) is a first-order process. The rate constant for the decomposition at 660 K is 4.5 × 10^–2 s^–1. (a) If we begin with an initial SO₂Cl₂ pressure of 450 torr, what is the pressure of this substance after 60 s?(b) At what time will the pressure of SO₂Cl₂ decline to one-tenth its initial value?

14.46 The first-order rate constant for the decomposition of N₂O₅, 2 N₂O₅(g) → 4 NO₂(g) + O₂(g), at 70 °C is 6.82 × 10^–3 s^–1. Suppose we start with 0.0250 mol of N₂O₅(g) in a volume of 2.0 L. (a) How many moles of N₂O₅ will remain after 5.0 min? (b) How many minutes will it take for the quantity of N₂O₅ to drop to 0.010 mol? (c) What is the half-life of N₂O₅ at 70 °C?

______

14.47 The reaction

SO₂Cl₂(g) → SO₂(g) + Cl₂(g)

is first order in SO₂Cl₂. Using the following kinetic data, determine the magnitude and units of the first-order rate constant:

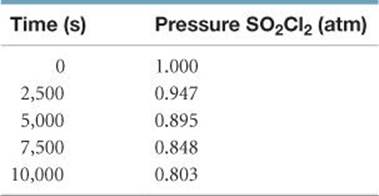
14.48 From the following data for the first-order gas-phase isomerization of CH₃NC at 215 °C, calculate the first-order rate constant and half-life for the reaction:

______

14.49 Consider the data presented in Exercise 14.19. (a) By using appropriate graphs, determine whether the reaction is first order or second order. (b) What is the rate constant for the reaction? (c) What is the half-life for the reaction?

14.50 Consider the data presented in Exercise 14.20. (a) Determine whether the reaction is first order or second order. (b) What is the rate constant? (c) What is the half-life?

______

14.51 The gas-phase decomposition of NO₂, 2 NO₂(g) → 2 NO(g) + O₂(g), is studied at 383 °C, giving the following data:

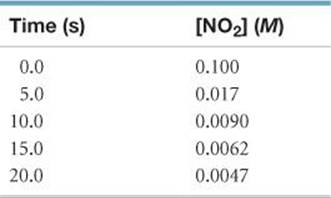
(a) Is the reaction first order or second order with respect to the concentration of NO₂? (b) What is the rate constant? (c) If you used the method of initial rates to obtain the order for NO₂, predict what reaction rates you would measure in the beginning of the reaction for initial concentrations of 0.200 M, 0.100 M, and 0.050 M NO₂.

14.52 Sucrose (C₁₂H₂₂O₁₁), commonly known as table sugar, reacts in dilute acid solutions to form two simpler sugars, glucose and fructose, both of which have the formula C₆H₁₂O₆. At 23 °C and in 0.5 M HCl, the following data were obtained for the disappearance of sucrose:

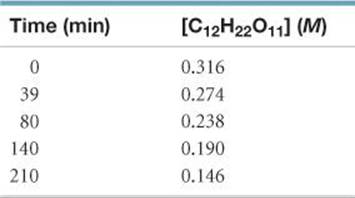
(a) Is the reaction first order or second order with respect to [C₁₂H₂₂O₁₁]? (b) What is the rate constant? (c) Using this rate constant, calculate the concentration of sucrose at 39, 80, 140, and 210 min if the initial sucrose concentration was 0.316 M and the reaction was zero order in sucrose.

TEMPERATURE AND RATE (section 14.5)

14.53 (a) What factors determine whether a collision between two molecules will lead to a chemical reaction? (b) According to the collision model, why does temperature affect the value of the rate constant? (c) Does the rate constant for a reaction generally increase or decrease with an increase in reaction temperature?

14.54 (a) In which of the following reactions would you expect the orientation factor to be least important in leading to reaction: NO + O → NO₂ or H + Cl → HCl? (b) How does the kinetic-molecular theory help us understand the temperature dependence of chemical reactions?

______

14.55 Calculate the fraction of atoms in a sample of argon gas at 400 K that has an energy of 10.0 kJ or greater.

14.56 (a) The activation energy for the isomerization of methyl isonitrile (Figure 14.7) is 160 kJ/mol. Calculate the fraction of methyl isonitrile molecules that has an energy of 160.0 kJ or greater at 500 K. (b) Calculate this fraction for a temperature of 520 K. What is the ratio of the fraction at 520 K to that at 500 K?

______

14.57 The gas-phase reaction Cl(g) + HBr(g) → HCl(g) + Br(g) has an overall enthalpy change of —66 kJ. The activation energy for the reaction is 7 kJ. (a) Sketch the energy profile for the reaction, and label E_a and ΔE. (b) What is the activation energy for the reverse reaction?

14.58 For the elementary process N₂O₅(g) → NO₂(g) + NO₃(g) the activation energy (E_a) and overall ΔE are 154 kJ/mol and 136 kJ/mol, respectively. (a) Sketch the energy profile for this reaction, and label E_a and ΔE. (b) What is the activation energy for the reverse reaction?

______

14.59 Indicate whether each statement is true or false. If it is false, rewrite it so that it is true.

(a) If you compare two reactions with similar collision factors, the one with the larger activation energy will be faster.

(b) A reaction that has a small rate constant must have a small frequency factor.

(c) Increasing the reaction temperature increases the fraction of successful collisions between reactants.

14.60 Indicate whether each statement is true or false. If it is false, rewrite it so that it is true.

(a) If you measure the rate constant for a reaction at different temperatures, you can calculate the overall enthalpy change for the reaction.

(b) Exothermic reactions are faster than endothermic reactions.

(c) If you double the temperature for a reaction, you cut the activation energy in half.

______

14.61 Based on their activation energies and energy changes and assuming that all collision factors are the same, which of the following reactions would be fastest and which would be slowest? Explain your answer.

(a) E_a = 45 kJ/mol; ΔE = –25 kJ/mol

(b) E_a = 35 kJ/mol; ΔE = –10 kJ/mol

(c) E_a = 55 kJ/mol; ΔE = 10 kJ/mol

14.62 Which of the reactions in Exercise 14.61 will be fastest in the reverse direction? Which will be slowest? Explain.

______

14.63 (a) A certain first-order reaction has a rate constant of 2.75 × 10^–2 s^–1 at 20 °C. What is the value of k at 60 °C if E_a = 75.5 kJ/mol? (b) Another first-order reaction also has a rate constant of 2.75 × 10^–2 s^–1 at 20 °C. What is the value of k at 60 °C if E_a = 125 kJ/mol? (c) What assumptions do you need to make in order to calculate answers for parts (a) and (b)?

14.64 Understanding the high-temperature behavior of nitrogen oxides is essential for controlling pollution generated in automobile engines. The decomposition of nitric oxide (NO) to N₂ and O₂ is second order with a rate constant of 0.0796 M^–1 s^–1 at 737 °C and 0.0815 M^–1 s^–1 at 947 °C. Calculate the activation energy for the reaction.

______

14.65 The rate of the reaction

CH₃COOC₂H₅(aq) + OH^–(aq) → CH₃COO^–(aq) + C₂H₅OH(aq)

was measured at several temperatures, and the following data were collected:

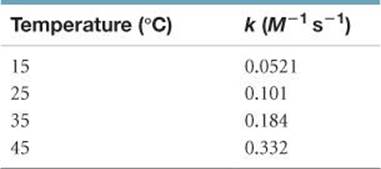
Calculate the value of E_a by constructing an appropriate graph.

14.66 The temperature dependence of the rate constant for a reaction is tabulated as follows:

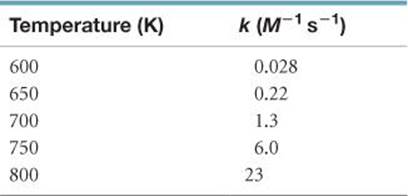
Calculate E_a and A.

______

[14.67] The activation energy of a certain reaction is 65.7 kJ/mol. How many times faster will the reaction occur at 50 °C than at 0 °C? State the assumptions you need to make in order to perform this calculation.

[14.68] The following is a quote from an article in the August 18,1998, issue of The New York Times about the breakdown of cellulose and starch: “A drop of 18 degrees Fahrenheit [from 77 °F to 59 °F] lowers the reaction rate six times; a 36-degree drop [from 77 °F to 41 °F] produces a fortyfold decrease in the rate.” (a) Calculate activation energies for the breakdown process based on the two estimates of the effect of temperature on rate. Are the values consistent? (b) Assuming the value of E_a calculated from the 36-degree drop and that the rate of breakdown is first order with a half-life at 25 °C of 2.7 years, calculate the half-life for breakdown at a temperature of –15 °C.

REACTION MECHANISMS (section 14.6)

14.69 (a) What is meant by the term elementary reaction? (b) What is the difference between a unimolecular and a bimolecular elementary reaction? (c) What is a reaction mechanism?

14.70 (a) What is meant by the term molecularity? (b) Why are termolecular elementary reactions so rare? (c) What is an intermediate in a mechanism?

______

14.71 What are the differences between an intermediate and a transition state?

14.72 What is meant by the term rate-determining step?

______

14.73 What is the molecularity of each of the following elementary reactions? Write the rate law for each.

(a) Cl₂(g) → 2 Cl(g)

(b) OCl^–(aq) + H₂O(l) → HOCl(aq) + OH^–(aq)

(c) NO(g) + Cl₂(g) → NOCl₂(g)

14.74 What is the molecularity of each of the following elementary reactions? Write the rate law for each.

(a) 2 NO(g) → N₂O₂(g)

(c) SO₃(g) → SO₂(g) + O(g)

______

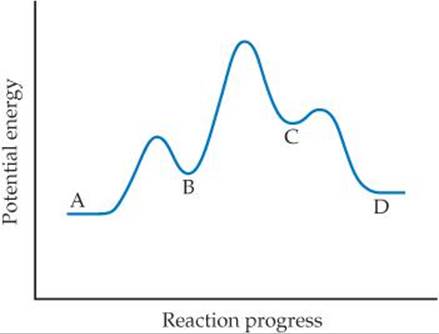
14.75 (a) Based on the following reaction profile, how many intermediates are formed in the reaction A → D? (b) How many transition states are there? (c) Which step is the fastest? (d) Is the reaction A → D exothermic or endothermic?

14.76 Consider the following energy profile.

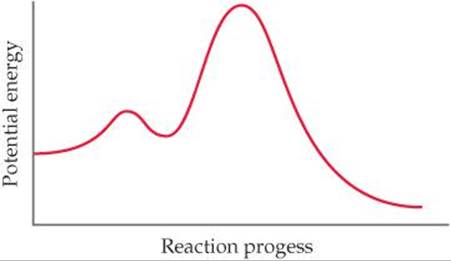
(a) How many elementary reactions are in the reaction mechanism? (b) How many intermediates are formed in the reaction? (c) Which step is rate limiting? (d) Is the overall reaction exothermic or endothermic?

______

14.77 The following mechanism has been proposed for the gas-phase reaction of H₂ with ICl:

H₂(g) + ICl(g) → HI(g) + HCl(g)

HI(g) + ICl(g) → I₂(g) + HCl(g)

(a) Write the balanced equation for the overall reaction. (b) Identify any intermediates in the mechanism. (c) If the first step is slow and the second one is fast, which rate law do you expect to be observed for the overall reaction?

14.78 The decomposition of hydrogen peroxide is catalyzed by iodide ion. The catalyzed reaction is thought to proceed by a two-step mechanism:

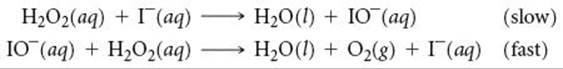
(a) Write the chemical equation for the overall process. (b) Identify the intermediate, if any, in the mechanism. (c) Assuming that the first step of the mechanism is rate determining, predict the rate law for the overall process.

______

14.79 The reaction 2 NO(g) + Cl₂(g) → 2 NOCl(g) was performed and the following data obtained:

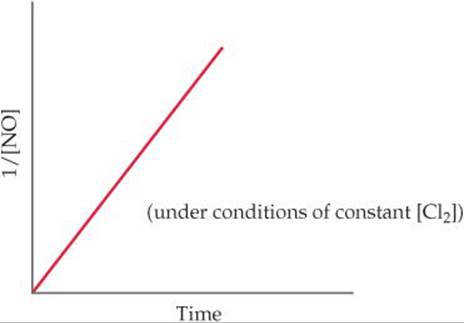
Is the following mechanism consistent with the data? Explain.

NO(g) + Cl₂(g) → NOCl₂(g)

NOCl₂(g) + NO(g) → 2 NOCl(g)

14.80 You have studied the gas-phase oxidation of HBr by O₂:

4 HBr(g) + O₂(g) → 2 H₂O(g) + 2 Br₂(g)

You find the reaction to be first order with respect to HBr and first order with respect to O₂. You propose the following mechanism:

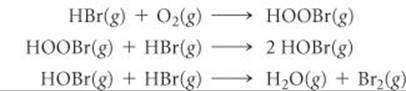
(a) Confirm that the elementary reactions add to give the overall reaction. (b) Based on the experimentally determined rate law, which step is rate determining? (c) What are the intermediates in this mechanism? (d) If you are unable to detect HOBr or HOOBr among the products, does this disprove your mechanism?

CATALYSIS (section 14.7)

14.81 (a) What is a catalyst? (b) What is the difference between a homogeneous and a heterogeneous catalyst? (c) Do catalysts affect the overall enthalpy change for a reaction, the activation energy, or both?

14.82 (a) Most commercial heterogeneous catalysts are extremely finely divided solid materials. Why is particle size important? (b) What role does adsorption play in the action of a heterogeneous catalyst?

______

[14.83] Platinum nanoparticles of diameter ˜2 nm are important catalysts in carbon monoxide oxidation to carbon dioxide. Platinum crystallizes in a face-centered cubic arrangement with an edge length of 3.924 Å. (a) Estimate how many platinum atoms would fit into a 2.0-nm sphere; the volume of a sphere is (4/3)πr³. Recall that 1Å = 1 × 10^–10 m and 1 nm = 1 × 10^–9 m. (b) Estimate how many platinum atoms are on the surface of a 2.0-nm Pt sphere, using the surface area of a sphere (4πr²) and assuming that the “footprint” of one Pt atom can be estimated from its atomic diameter of 2.8 Å. (c) Using your results from (a) and (b), calculate the percentage of Pt atoms that are on the surface of a 2.0-nm nanoparticle. (d) Repeat these calculations for a 5.0-nm platinum nanoparticle. (e) Which size of nanoparticle would you expect to be more catalytically active and why?

14.84 In solution, chemical species as simple as H+ and OH– can serve as catalysts for reactions. Imagine you could measure the [H⁺] of a solution containing an acid-catalyzed reaction as it occurs. Assume the reactants and products themselves are neither acids nor bases. Sketch the [H⁺] concentration profile you would measure as a function of time for the reaction, assuming t = 0 is when you add a drop of acid to the reaction.

______

14.85 The oxidation of SO₂ to SO₃ is catalyzed by NO₂. The reaction proceeds according to:

(a) Show that the two reactions can be summed to give the overall oxidation of SO₂ by O₂ to give SO₃. (b) Why do we consider NO₂ a catalyst and not an intermediate in this reaction? (c) Is this an example of homogeneous catalysis or heterogeneous catalysis?

14.86 NO catalyzes the decomposition of N₂O, possibly by the following mechanism:

(a) What is the chemical equation for the overall reaction? Show how the two steps can be added to give the overall equation. (b) Why is NO considered a catalyst and not an intermediate? (c) If experiments show that during the decomposition of N₂O, NO₂ does not accumulate in measurable quantities, does this rule out the proposed mechanism? If you think not, suggest what might be going on.

______

14.87 Many metallic catalysts, particularly the precious-metal ones, are often deposited as very thin films on a substance of high surface area per unit mass, such as alumina (Al₂O₃) or silica (SiO₂). (a) Why is this an effective way of utilizing the catalyst material compared to having powdered metals? (b) How does the surface area affect the rate of reaction?

14.88 (a) If you were going to build a system to check the effectiveness of automobile catalytic converters on cars, what substances would you want to look for in the car exhaust? (b) Automobile catalytic converters have to work at high temperatures, as hot exhaust gases stream through them. In what ways could this be an advantage? In what ways a disadvantage? (c) Why is the rate of flow of exhaust gases over a catalytic converter important?

______

14.89 When D₂ reacts with ethylene (C₂H₄) in the presence of a finely divided catalyst, ethane with two deuteriums, CH₂D—CH₂D, is formed. (Deuterium, D, is an isotope of hydrogen of mass 2). Very little ethane forms in which two deuteriums are bound to one carbon (for example, CH₃—CHD₂). Use the sequence of steps involved in the reaction (Figure 14.24) to explain why this is so.

14.90 Heterogeneous catalysts that perform hydrogenation reactions, as illustrated in Figure 14.24, are subject to “poisoning,” which shuts down their catalytic ability. Compounds of sulfur are often poisons. Suggest a mechanism by which such compounds might act as poisons.

______

14.91 (a) Explain the importance of enzymes in biological systems. (b) What chemical transformations are catalyzed (i) by the enzyme catalase, (ii) by nitrogenase? (c) Many enzymes follow this generic reaction mechanism, where E is enzyme, S is substrate, ES is the enzyme-substrate complex (where the substrate is bound to the enzyme's active site), and P is the product:

What assumptions are made in this model with regard to the rate of the bound substrate being chemically transformed into bound product in the active site?

14.92 There are literally thousands of enzymes at work in complex living systems such as human beings. What properties of enzymes give rise to their ability to distinguish one substrate from another?

______

14.93 The enzyme carbonic anhydrase catalyzes the reaction CO₂(g) + H₂O(l) → HCO₃^–(aq) + H⁺(aq). In water, without the enzyme, the reaction proceeds with a rate constant of 0.039 s at 25 °C. In the presence of the enzyme in water, the reaction proceeds with a rate constant of 1.0 × 10⁶ s^–1 at 25 °C. Assuming the collision factor is the same for both situations, calculate the difference in activation energies for the uncatalyzed versus enzyme-catalyzed reaction.

14.94 The enzyme urease catalyzes the reaction of urea, (NH₂CONH₂), with water to produce carbon dioxide and ammonia. In water, without the enzyme, the reaction proceeds with a first-order rate constant of 4.15 × 10^–5 s^–1 at 100 °C. In the presence of the enzyme in water, the reaction proceeds with a rate constant of 3.4 × 10⁴ s^–1 at 21 °C. (a) Write out the balanced equation for the reaction catalyzed by urease. (b) Assuming the collision factor is the same for both situations, estimate the difference in activation energies for the uncatalyzed versus enzyme-catalyzed reaction.

______

[14.95] The activation energy of an uncatalyzed reaction is 95 kJ/mol. The addition of a catalyst lowers the activation energy to 55 kJ/mol. Assuming that the collision factor remains the same, by what factor will the catalyst increase the rate of the reaction at (a) 25 °C, (b) 125 °C?

[14.96] Suppose that a certain biologically important reaction is quite slow at physiological temperature (37 °C) in the absence of a catalyst. Assuming that the collision factor remains the same, by how much must an enzyme lower the activation energy of the reaction in order to achieve a 1 × 10⁵-fold increase in the reaction rate?

ADDITIONAL EXERCISES

14.97 Explain why rate laws generally cannot be written from balanced equations. Under what circumstance is the rate law related directly to the balanced equation for a reaction?

14.98 Hydrogen sulfide (H₂S) is a common and troublesome pollutant in industrial wastewaters. One way to remove H₂S is to treat the water with chlorine, in which case the following reaction occurs:

H₂S(aq) + Cl₂(aq) → S(s) + 2 H⁺(aq) + 2 Cl^–(aq)

The rate of this reaction is first order in each reactant. The rate constant for the disappearance of H₂S at 28 °C is 3.5 × 10^–2M^–1 s^–1. If at a given time the concentration of H₂S is 2.0 × 10^–4M and that of Cl₂ is 0.025 M, what is the rate of formation of Cl^–?

14.99 The reaction 2 NO(g) + O₂(g) → 2 NO₂(g) is second order in NO and first order in O₂. When [NO] = 0.040 M and [O₂] = 0.035 M, the observed rate of disappearance of NO is 9.3 × 10^–5M/s. (a) What is the rate of disappearance of O₂ at this moment? (b) What is the value of the rate constant? (c) What are the units of the rate constant? (d) What would happen to the rate if the concentration of NO were increased by a factor of 1.8?

14.100 Consider the following reaction between mercury(II) chloride and oxalate ion:

2 HgCl₂(aq) + C₂O₄^2–(aq) → 2 Cl^–(aq) + 2 CO₂(g) + Hg₂Cl₂(s)

The initial rate of this reaction was determined for several concentrations of HgCl₂ and C₂O₄^2–, and the following rate data were obtained for the rate of disappearance of C₂O₄^2–:

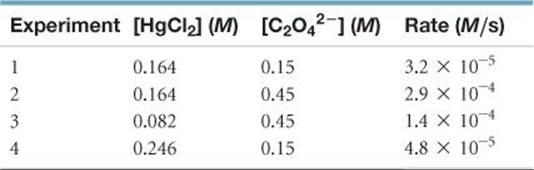
(a) What is the rate law for this reaction? (b) What is the value of the rate constant with proper units? (c) What is the reaction rate when the initial concentration of HgCl₂ is 0.100 M and that of (C₂O₄^2–) is 0.25 M if the temperature is the same as that used to obtain the data shown?

14.101 The reaction 2 NO₂ → 2 NO + O₂ has the rate constant k = 0.63 M^–1 s^–1. Based on the units for k, is the reaction first or second order in NO₂? If the initial concentration of NO₂ is 0.100 M, how would you determine how long it would take for the concentration to decrease to 0.025 M?

14.102 Consider two reactions. Reaction (1) has a constant half-life, whereas reaction (2) has a half-life that gets longer as the reaction proceeds. What can you conclude about the rate laws of these reactions from these observations?

[14.103] When chemists are performing kinetics experiments, the general rule of thumb is to allow the reaction to proceed for 4 half-lives. (a) Explain how you would be able to tell that the reaction has proceeded for 4 half-lives. (b) Let us suppose a reaction A → B takes 6 days to proceed for 4 half-lives and is first order in A. However, when your lab partner performs this reaction for the first time, he does not realize how long it takes, and he stops taking kinetic data, monitoring the loss of A, after only 2 hours. Your lab partner concludes the reaction is zero order in A based on the data. Sketch a graph of [A] versus time to convince your lab partner the two of you need to be in the lab for a few days to obtain the proper rate law for the reaction.

14.104 (a) The reaction H₂O₂(aq) → H₂O(l) + ½ O₂(g) is first order. Near room temperature, the rate constant equals 7.0 × 10^–4 s^–1. Calculate the half-life at this temperature. (b) At 415 °C, (CH₂)₂O decomposes in the gas phase, (CH₂)₂O(g) → CH₄(g) + CO(g). If the reaction is first order with a half-life of 56.3 min at this temperature, calculate the rate constant in s^–1.

14.105 Americium-241 is used in smoke detectors. It has a first order rate constant for radioactive decay of k = 1.6 × 10^–3 yr^–1. By contrast, iodine-125, which is used to test for thyroid functioning, has a rate constant for radioactive decay of k = 0.011 day^–1. (a) What are the half-lives of these two isotopes? (b) Which one decays at a faster rate? (c) How much of a 1.00-mg sample of each isotope remains after 3 half-lives? (d) How much of a 1.00-mg sample of each isotope remains after 4 days?

14.106 Urea (NH₂CONH₂) is the end product in protein metabolism in animals. The decomposition of urea in 0.1 M HCl occurs according to the reaction

NH₂CONH₂(aq) + H⁺(aq) + 2 H₂O(l) → 2 NH₄ + (aq) + HCO₃^–(aq)

The reaction is first order in urea and first order overall. When [NH₂CONH₂] = 0.200 M, the rate at 61.05 °C is 8.56 × 10^–5M/s. (a) What is the rate constant, k? (b) What is the concentration of urea in this solution after 4.00 × 10³ s if the starting concentration is 0.500 M? (c) What is the half-life for this reaction at 61.05 °C?

14.107 The rate of a first-order reaction is followed by spectroscopy, monitoring the absorbance of a colored reactant at 520 nm. The reaction occurs in a 1.00-cm sample cell, and the only colored species in the reaction has an extinction coefficient of 5.60 × 10³M^–1 cm^–1 at 520 nm. (a)Calculate the initial concentration of the colored reactant if the absorbance is 0.605 at the beginning of the reaction. (b) The absorbance falls to 0.250 at 30.0 min. Calculate the rate constant in units of s^–1. (c) Calculate the half-life of the reaction. (d) How long does it take for the absorbance to fall to 0.100?

[14.108] A colored dye compound decomposes to give a colorless product. The original dye absorbs at 608 nm and has an extinction coefficient of 4.7 × 10⁴M^–1cm^–1 at that wavelength. You perform the decomposition reaction in a 1-cm cuvette in a spectrometer and obtain the following data:

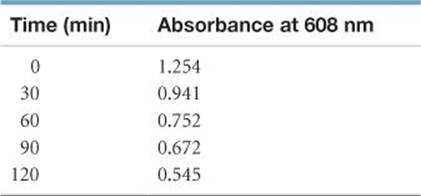
From these data, determine the rate law for the reaction “dye → product” and determine the rate constant.

14.109 Cyclopentadiene (C₅H₆) reacts with itself to form dicyclopentadiene (C₁₀H₁₂). A 0.0400 M solution of C₅H₆ was monitored as a function of time as the reaction 2 C₅H₆ → C₁₀H₁₂ proceeded. The following data were collected:

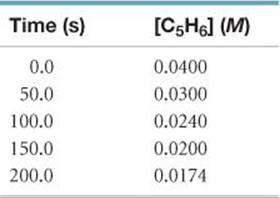
Plot [C₅H₆] versus time, ln [C₅H₆] versus time, and 1/[C₅H₆] versus time. What is the order of the reaction? What is the value of the rate constant?

14.110 (a) Two reactions have identical values for E_a. Does this ensure that they will have the same rate constant if run at the same temperature? Explain. (b) Two similar reactions have the same rate constant at 25 °C, but at 35 °C one of the reactions has a larger rate constant than the other. Account for these observations.

14.111 The first-order rate constant for reaction of a particular organic compound with water varies with temperature as follows:

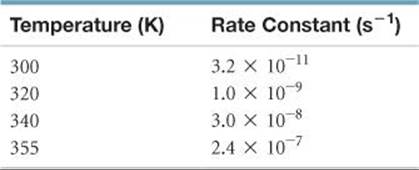
From these data, calculate the activation energy in units of kJ/mol.

14.112 The following mechanism has been proposed for the reaction of NO with H₂ to form N₂O and H₂O:

(a) Show that the elementary reactions of the proposed mechanism add to provide a balanced equation for the reaction. (b) Write a rate law for each elementary reaction in the mechanism. (c) Identify any intermediates in the mechanism. (d) The observed rate law is rate =k[NO]²[H₂]. If the proposed mechanism is correct, what can we conclude about the relative speeds of the first and second reactions?

14.113 Ozone in the upper atmosphere can be destroyed by the following two-step mechanism:

Cl(g) + O₃(g) → ClO(g) + O₂(g)

ClO(g) + O(g) → Cl(g) + O₂(g)

(a) What is the overall equation for this process? (b) What is the catalyst in the reaction? How do you know? (c) What is the intermediate in the reaction? How do you distinguish it from the catalyst?

14.114 Using Figure 14.23 as your basis, draw the energy profile for the bromide–catalyzed decomposition of hydrogen peroxide. (a) Label the curve with the activation energies for reactions [14.30] and [14.31]. (b) Notice from Figure 14.22 that when Br^–(aq) is first added, Br₂accumulates to some extent during the reaction and the solution turns brown. What does this tell us about the relative rates of the reactions represented by Equations 14.30 and 14.31?

[14.115] The following mechanism has been proposed for the gas-phase reaction of chloroform (CHCl₃) and chlorine:

Step 1: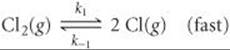

Step 2:

Step 3:

(a) What is the overall reaction? (b) What are the intermediates in the mechanism? (c) What is the molecularity of each of the elementary reactions? (d) What is the rate-determining step? (e) What is the rate law predicted by this mechanism? (Hint: The overall reaction order is not an integer.)

[14.116] In a hydrocarbon solution, the gold compound (CH₃)₃AuPH₃ decomposes into ethane (C₂H₆) and a different gold compound, (CH₃)AuPH₃. The following mechanism has been proposed for the decomposition of (CH₃)₃AuPH₃:

Step 1:

Step 2:

Step 3:

(a) What is the overall reaction? (b) What are the intermediates in the mechanism? (c) What is the molecularity of each of the elementary steps? (d) What is the rate-determining step? (e) What is the rate law predicted by this mechanism? (f) What would be the effect on the reaction rate of adding PH₃ to the solution of (CH₃)₃AuPH₃?

14.117 One of the many remarkable enzymes in the human body is carbonic anhydrase, which catalyzes the interconversion of carbon dioxide and water with bicarbonate ion and protons. If it were not for this enzyme, the body could not rid itself rapidly enough of the CO₂ accumulated by cell metabolism. The enzyme catalyzes the dehydration (release to air) of up to 10⁷ CO₂ molecules per second. Which components of this description correspond to the terms enzyme, substrate, and turnover number?

14.118 Enzymes are often described as following the two-step mechanism:

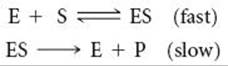
where E = enzyme, S = substrate, ES = enzyme-substrate complex, and P = product.

(a) If an enzyme follows this mechanism, what rate law is expected for the reaction? (b) Molecules that can bind to the active site of an enzyme but are not converted into product are called enzyme inhibitors. Write an additional elementary step to add into the preceding mechanism to account for the reaction of E with I, an inhibitor.

INTEGRATIVE EXERCISES

14.119 Dinitrogen pentoxide (N₂O₅) decomposes in chloroform as a solvent to yield NO₂ and O₂. The decomposition is first order with a rate constant at 45 °C of 1.0 × 10^–5 s^–1. Calculate the partial pressure of O₂ produced from 1.00 L of 0.600 M N₂O₅ solution at 45 °C over a period of 20.0 hr if the gas is collected in a 10.0-L container. (Assume that the products do not dissolve in chloroform.)

[14.120] The reaction between ethyl iodide and hydroxide ion in ethanol (C₂H₅OH) solution, C₂H₅I(alc) + OH^–(alc) → C₂H₅OH(l) + I^–(alc), has an activation energy of 86.8 kJ/mol and a frequency factor of 2.10 × 10¹¹M^–1 s^–1. (a) Predict the rate constant for the reaction at 35 °C. (b) A solution of KOH in ethanol is made up by dissolving 0.335 g KOH in ethanol to form 250.0 mL of solution. Similarly, 1.453 g of C₂H₅I is dissolved in ethanol to form 250.0 mL of solution. Equal volumes of the two solutions are mixed. Assuming the reaction is first order in each reactant, what is the initial rate at 35 °C? (c) Which reagent in the reaction is limiting, assuming the reaction proceeds to completion? (d) Assuming the frequency factor and activation energy do not change as a function of temperature, calculate the rate constant for the reaction at 50 °C.

[14.121] You obtain kinetic data for a reaction at a set of different temperatures. You plot ln k versus 1/T and obtain the following graph:

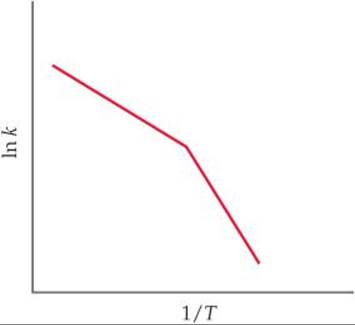
Suggest a molecular-level interpretation of these unusual data.

14.122 The gas-phase reaction of NO with F₂ to form NOF and F has an activation energy of E_a = 6.3 kJ/mol and a frequency factor of A = 6.0 × 10⁸M^–1 s^–1. The reaction is believed to be bimolecular:

NO(g) + F₂(g) → NOF(g) + F(g)

(a) Calculate the rate constant at 100 °C. (b) Draw the Lewis structures for the NO and the NOF molecules, given that the chemical formula for NOF is misleading because the nitrogen atom is actually the central atom in the molecule. (c) Predict the shape for the NOF molecule. (d)Draw a possible transition state for the formation of NOF, using dashed lines to indicate the weak bonds that are beginning to form. (e) Suggest a reason for the low activation energy for the reaction.

14.123 The mechanism for the oxidation of HBr by O₂ to form 2 H₂O and Br₂ is shown in Exercise 14.80. (a) Calculate the overall standard enthalpy change for the reaction process. (b) HBr does not react with O₂ at a measurable rate at room temperature under ordinary conditions. What can you infer from this about the magnitude of the activation energy for the rate-determining step? (c) Draw a plausible Lewis structure for the intermediate HOOBr. To what familiar compound of hydrogen and oxygen does it appear similar?

[14.124] The rates of many atmospheric reactions are accelerated by the absorption of light by one of the reactants. For example, consider the reaction between methane and chlorine to produce methyl chloride and hydrogen chloride:

Reaction 1: CH₄(g) + Cl₂(g) → CH₃Cl(g) + HCl(g)

This reaction is very slow in the absence of light. However, Cl₂(g) can absorb light to form Cl atoms:

Reaction 2: Cl₂(g) + hv → 2 Cl(g)

Once the Cl atoms are generated, they can catalyze the reaction of CH₄ and Cl₂, according to the following proposed mechanism:

Reaction 3: CH₄(g) + Cl(g) → CH₃(g) + HCl(g)

Reaction 4: CH₃(g) + Cl₂(g) → CH₃Cl(g) + Cl(g)

The enthalpy changes and activation energies for these two reactions are tabulated as follows:

(a) By using the bond enthalpy for Cl₂ (Table 8.4), determine the longest wavelength of light that is energetic enough to cause reaction 2 to occur. In which portion of the electromagnetic spectrum is this light found? (b) By using the data tabulated here, sketch a quantitative energy profile for the catalyzed reaction represented by reactions 3 and 4. (c) By using bond enthalpies, estimate where the reactants, CH₄(g) + Cl₂(g), should be placed on your diagram in part (b). Use this result to estimate the value of E_a for the reaction CH₄(g) + Cl₂(g) → CH₃(g) + HCl(g) + Cl(g). (d) The species Cl(g) and CH₃(g) in reactions 3 and 4 are radicals, that is, atoms or molecules with unpaired electrons. Draw a Lewis structure of CH₃, and verify that it is a radical. (e) The sequence of reactions 3 and 4 comprises a radical chain mechanism. Why do you think this is called a “chain reaction”? Propose a reaction that will terminate the chain reaction.

[14.125] Many primary amines, RNH₂, where R is a carbon-containing fragment such as CH₃, CH₃CH₂, and so on, undergo reactions where the transition state is tetrahedral. (a) Draw a hybrid orbital picture to visualize the bonding at the nitrogen in a primary amine (just use a C atom for “R”). (b) What kind of reactant with a primary amine can produce a tetrahedral intermediate?

[14.126] The NO_x waste stream from automobile exhaust includes species such as NO and NO₂. Catalysts that convert these species to N₂ are desirable to reduce air pollution. (a) Draw the Lewis dot and VSEPR structures of NO, NO₂, and N₂. (b) Using a resource such as Table 8.4, look up the energies of the bonds in these molecules. In what region of the electromagnetic spectrum are these energies? (c) Design a spectroscopic experiment to monitor the conversion of NO_x into N₂, describing what wavelengths of light need to be monitored as a function of time.