CHEMISTRY THE CENTRAL SCIENCE

15 CHEMICAL EQUILIBRIUM

15.2 THE EQUILIBRIUM CONSTANT

A reaction in which reactants convert to products and products convert to reactants in the same reaction vessel naturally leads to an equilibrium, regardless of how complicated the reaction is and regardless of the nature of the kinetic processes for the forward and reverse reactions. Consider the synthesis of ammonia from nitrogen and hydrogen:

This reaction is the basis for the Haber process, which is critical for the production of fertilizers and therefore critical to the world's food supply. In the Haber process, N₂ and H₂ react at high pressure and temperature in the presence of a catalyst to form ammonia. In a closed system, however, the reaction does not lead to complete consumption of the N₂ and H₂. Rather, at some point the reaction appears to stop with all three components of the reaction mixture present at the same time.

How the concentrations of H₂, N₂, and NH₃ vary with time is shown in FIGURE 15.3. Notice that an equilibrium mixture is obtained regardless of whether we begin with N₂ and H₂ or with NH₃. The equilibrium condition is reached from either direction.

GIVE IT SOME THOUGHT

How do we know when equilibrium has been reached in a chemical reaction?

An expression similar to Equation 15.5 governs the concentrations of N₂, H₂, and NH₃ at equilibrium. If we were to systematically change the relative amounts of the three gases in the starting mixture and then analyze each equilibrium mixture, we could determine the relationship among the equilibrium concentrations.

Chemists carried out studies of this kind on other chemical systems in the nineteenth century before Haber's work. In 1864, Cato Maximilian Guldberg (1836–1902) and Peter Waage (1833–1900) postulated their law of mass action, which expresses, for any reaction, the relationship between the concentrations of the reactants and products present at equilibrium. Suppose we have the general equilibrium equation

where A, B, D, and E are the chemical species involved and a, b, d, and e are their coefficients in the balanced chemical equation. According to the law of mass action, the equilibrium condition is described by the expression

We call this relationship the equilibrium-constant expression (or merely the equilibrium expression) for the reaction. The constant K_c, the equilibrium constant, is the numerical value obtained when we substitute molar equilibrium concentrations into the equilibrium-constant expression. The subscript c on the K indicates that concentrations expressed in molarity are used to evaluate the constant.

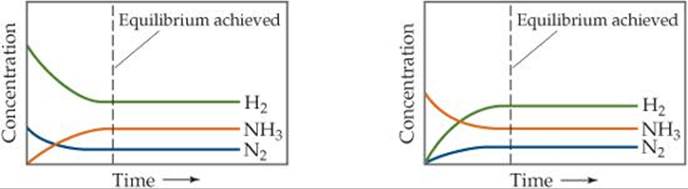
FIGURE 15.3 The same equilibrium is reached whether we start with only reactants (N₂ and H₂) or with only product (NH₃).

CHEMISTRY PUT TO WORK
The Haber Process

The quantity of food required to feed the ever-increasing human population far exceeds that provided by nitrogen-fixing plants. (Section 14.7) Therefore, human agriculture requires substantial amounts of ammonia-based fertilizers for croplands. Of all the chemical reactions that humans have learned to control for their own purposes, the synthesis of ammonia from hydrogen and atmospheric nitrogen is one of the most important.

In 1912 the German chemist Fritz Haber (1868–1934) developed the Haber process (Equation 15.6). The process is sometimes also called the Haber-Bosch process to honor Karl Bosch, the engineer who developed the industrial process on a large scale. The engineering needed to implement the Haber process requires the use of temperatures and pressures (approximately 500 °C and 200 to 600 atm) that were difficult to achieve at that time.

FIGURE 15.4 Liquid ammonia used as fertilizer by direct injection into soil.

The Haber process provides a historically interesting example of the complex impact of chemistry on our lives. At the start of World War I, in 1914, Germany depended on nitrate deposits in Chile for the nitrogen-containing compounds needed to manufacture explosives. During the war, the Allied naval blockade of South America cut off this supply. However, by using the Haber reaction to fix nitrogen from air, Germany was able to continue to produce explosives. Experts have estimated that World War I would have ended before 1918 had it not been for the Haber process.

From these unhappy beginnings as a major factor in international warfare, the Haber process has become the world's principal source of fixed nitrogen. The same process that prolonged World War I has enabled the manufacture of fertilizers that have increased crop yields, thereby saving millions of people from starvation. About 40 billion pounds of ammonia are manufactured annually in the United States, mostly by the Haber process. The ammonia can be applied directly to the soil (FIGURE 15.4), or it can be converted into ammonium salts that are also used as fertilizers. Haber was a patriotic German who gave enthusiastic support to his nation's war effort. He served as chief of Germany's Chemical Warfare Service during World War I and developed the use of chlorine as a poison-gas weapon. Consequently, the decision to award him the Nobel Prize in Chemistry in 1918 was the subject of considerable controversy and criticism. The ultimate irony, however, came in 1933 when Haber was expelled from Germany because he was Jewish.

RELATED EXERCISES: 15.46 and 15.76

The numerator of the equilibrium-constant expression is the product of the concentrations of all substances on the product side of the equilibrium equation, each raised to a power equal to its coefficient in the balanced equation. The denominator is similarly derived from the reactant side of the equilibrium equation. Thus, for the Haber process, the equilibrium-constant expression is

Once we know the balanced chemical equation for a reaction that reaches equilibrium, we can write the equilibrium-constant expression even if we do not know the reaction mechanism. The equilibrium-constant expression depends only on the stoichiom-etry of the reaction, not on its mechanism.

The value of the equilibrium constant at any given temperature does not depend on the initial amounts of reactants and products. It also does not matter whether other substances are present, as long as they do not react with a reactant or a product. The value of K_c depends only on the particular reaction and on the temperature.

SAMPLE EXERCISE 15.1 Writing Equilibrium-Constant Expressions

Write the equilibrium expression for K_c for the following reactions:

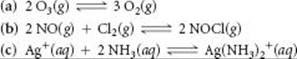
SOLUTION

Analyze We are given three equations and are asked to write an equilibrium-constant expression for each.

Plan Using the law of mass action, we write each expression as a quotient having the product concentration terms in the numerator and the reactant concentration terms in the denominator. Each concentration term is raised to the power of its coefficient in the balanced chemical equation.

Solve

PRACTICE EXERCISE

Write the equilibrium-constant expression K_c for

Answers: (a)

Evaluating K_c

We can illustrate how the law of mass action was discovered empirically and demonstrate that the equilibrium constant is independent of starting concentrations by examining a series of experiments involving dinitrogen tetroxide and nitrogen dioxide:

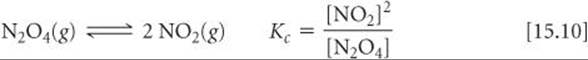
We start with several sealed tubes containing different concentrations of NO₂ and N₂O₄. The tubes are kept at 100 °C until equilibrium is reached. We then analyze the mixtures and determine the equilibrium concentrations of NO₂ and N₂O₄, which are shown in TABLE 15.1.

To evaluate K_c, we insert the equilibrium concentrations into the equilibrium-constant expression. For example, using Experiment 1 data, [NO₂] = 0.0172 M and [N₂O₄] = 0.00140 M, we find

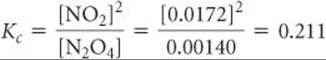
TABLE 15.1 • Initial and Equilibrium Concentrations of N₂O₄(g) and NO₂(g) at 100 °C

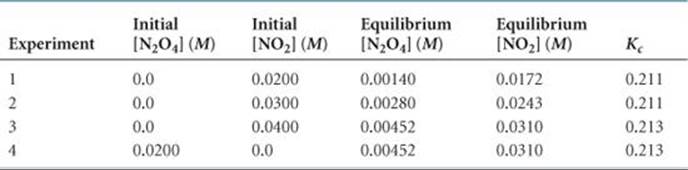
Proceeding in the same way, the values of K_c for the other samples are calculated. Note from Table 15.1 that the value for K_c is constant (within the limits of experimental error) even though the initial concentrations vary. Furthermore, Experiment 4 shows that equilibrium can be achieved beginning with N₂O₄ rather than with NO₂. That is, equilibrium can be approached from either direction. FIGURE 15.5 shows how Experiments 3 and 4 result in the same equilibrium mixture even though the two experiments start with very different NO₂ concentrations.

Notice that no units are given for K_c either in Table 15.1 or in the calculation we just did using Experiment 1 data. It is common practice to write equilibrium constants without units for reasons that we address later in this section.

Recall that we began our discussion of equilibrium in terms of rates. Equation 15.5 shows that K_c is equal to k_f/k_r, the ratio of the forward rate constant to the reverse rate constant. For the N₂O₄/NO₂ reaction, K_c = 0.212, which means that k_r is 4.72 times as large as k_f (since 1/0.212 = 4.72). It is not possible to obtain the absolute value of either rate constant knowing only the value of K_c.

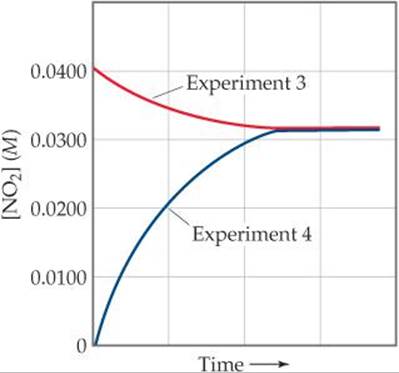
FIGURE 15.5 The same equilibrium mixture is produced regardless of the initial NO₂ concentration. The concentration of NO₂ either increases or decreases until equilibrium is reached.

GIVE IT SOME THOUGHT

How does the value of K_c in Equation 15.10 depend on the starting concentrations of NO₂ and N₂O₄?

Equilibrium Constants in Terms of Pressure, K_p

When the reactants and products in a chemical reaction are gases, we can formulate the equilibrium-constant expression in terms of partial pressures. When partial pressures in atmospheres are used in the expression, we denote the equilibrium constant K_p (where the subscript p stands for pressure). For the general reaction in Equation 15.7, we have

where P_A is the partial pressure of A in atmospheres, P_B is the partial pressure of B in atmospheres, and so forth. For example, for our N₂O₄/NO₂ reaction we have

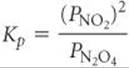
GIVE IT SOME THOUGHT

What is the difference between the equilibrium constant K_c and the equilibrium constant K_p?

For a given reaction, the numerical value of K_c is generally different from the numerical value of K_p. We must therefore take care to indicate, via subscript c or p, which constant we are using. It is possible, however, to calculate one from the other using the ideal-gas equation: (Section 10.4)

The usual units for n/V are mol/L, which equals molarity, M. For substance A in our generic reaction, we therefore see that

When we substitute Equation 15.13 and like expressions for the other gaseous components of the reaction into Equation 15.11, we obtain a general expression relating K_p and K_c:

The quantity Δn is the change in the number of moles of gas in the balanced chemical equation. It equals the sum of the coefficients of the gaseous products minus the sum of the coefficients of the gaseous reactants:

For example, in the reaction, there are two moles of product NO₂ and one mole of reactant N₂O₄. Therefore, Δn = 2 – 1 = 1, and K_p = K_c(RT) for this reaction.

From Equation 15.14, we see that K_p = K_c only when the same number of moles of gas appears on both sides of the balanced chemical equation, so that Δn = 0.

SAMPLE EXERCISE 15.2 Converting between K_c and K_p

For the Haber process,

K_c = 9.60 at 300 °C. Calculate K_p for this reaction at this temperature.

SOLUTION

Analyze We are given K_c for a reaction and asked to calculate K_p.

Plan The relationship between K_c and K_p is given by Equation 15.14. To apply that equation, we must determine Δn by comparing the number of moles of product with the number of moles of reactants (Equation 15.15).

Solve With 2 mol of gaseous products (2 NH₃) and 4 mol of gaseous reactants (1 N₂ + 3 H₂), Δn= 2 Δ 4 = Δ2. (Remember that Δ functions are always based on products minus reactants.) The temperature is 273 + 300 = 573 K. The value for the ideal-gas constant, R, is 0.08206 L-atm/mol-K. Using K_c = 9.60, we therefore have

PRACTICE EXERCISE

For the equilibrium at 1000 K. Calculate the value for K_p.

Answer: 0.335

Equilibrium Constants and Units

You may wonder why equilibrium constants are reported without units. The equilibrium constant is related to the kinetics of a reaction as well as to the thermodynamics. (We explore this latter connection in Chapter 19.) Equilibrium constants derived from thermodynamic measurements are defined in terms of activities rather than concentrations or partial pressures.

The activity of any substance in an ideal mixture is the ratio of the concentration or pressure of the substance either to a reference concentration (1 M) or to a reference pressure (1 atm). For example, if the concentration of a substance in an equilibrium mixture is 0.010 M, its activity is 0.010 M/1 M = 0.010. The units of such ratios always cancel and, consequently, activities have no units. Furthermore, the numerical value of the activity equals the concentration. For pure solids and pure liquids, the situation is even simpler because the activities then merely equal 1 (again with no units).

In real systems, activities are also ratios that have no units. Even though these activities may not be exactly numerically equal to concentrations, we will ignore the differences. All we need to know at this point is that activities have no units. As a result, the thermodynamic equilibrium constants derived from them also have no units. It is therefore common practice to write all types of equilibrium constants without units, a practice that we adhere to in this text. In more advanced chemistry courses, you may make more rigorous distinctions between concentrations and activities.

GIVE IT SOME THOUGHT

If the concentration of N₂O₄ in an equilibrium mixture is 0.00140 M, what is its activity? (Assume the solution is ideal.)