CHEMISTRY THE CENTRAL SCIENCE

15 CHEMICAL EQUILIBRIUM

15.4 HETEROGENEOUS EQUILIBRIA

Many equilibria involve substances that are all in the same phase, usually gas or liquid. Such equilibria are called homogeneous equilibria. In some cases, however, the substances in equilibrium are in different phases, giving rise to heterogeneous equilibria. As an example of the latter, consider the equilibrium that occurs when solid lead(II) chloride dissolves in water to form a saturated solution:

This system consists of a solid in equilibrium with two aqueous species. If we want to write the equilibrium-constant expression for this process, we encounter a problem we have not encountered previously: How do we express the concentration of a solid? Although we can express that concentration in moles per unit volume, it is unnecessary to do so in writing equilibrium-constant expressions. Whenever a pure solid or a pure liquid is involved in a heterogeneous equilibrium, its concentration is not included in the equilibrium-constant expression. Thus, the equilibrium-constant expression for the reaction of Equation 15.18 is

Even though PbCl₂(s) does not appear in the equilibrium-constant expression, it must be present for equilibrium to occur.

The fact that pure solids and pure liquids are excluded from equilibrium-constant expressions can be explained in two ways. First, the concentration of a pure solid or liquid has a constant value. If the mass of a solid is doubled, its volume also doubles. Thus, its concentration, which relates to the ratio of mass to volume, stays the same. Because equilibrium-constant expressions include terms only for reactants and products whose concentrations can change during a chemical reaction, the concentrations of pure solids and pure liquids are omitted.

The omission can also be rationalized in a second way. Recall from Section 15.2 that what is substituted into a thermodynamic equilibrium expression is the activity of each substance, which is a ratio of the concentration to a reference value. For a pure substance, the reference value is the concentration of the pure substance, so that the activity of any pure solid or liquid is always 1.

GO FIGURE

Imagine starting with only CaO in a bell jar and adding CO₂(g) to make its pressure the same as it is in these two bell jars. How does the equilibrium concentration of CO₂(g) in your jar compare with the CO₂(g) equilibrium concentration in these two jars?

FIGURE 15.7 At a given temperature, the equilibrium pressure of CO₂ in the bell jars is the same no matter how much of each solid is present.

GIVE IT SOME THOUGHT

Write the equilibrium-constant expression for the evaporation of water, H₂O(l) H₂O(g), in terms of partial pressures.

Decomposition of calcium carbonate is another example of a heterogeneous reaction:

Omitting the concentrations of the solids from the equilibrium-constant expression gives

These equations tell us that at a given temperature, an equilibrium among CaCO₃, CaO, and CO₂ always leads to the same CO₂ partial pressure as long as all three components are present. As shown in FIGURE 15.7, we have the same CO₂ pressure regardless of the relative amounts of CaO and CaCO₃.

SAMPLE EXERCISE 15.6 Writing Equilibrium-Constant Expressions for Heterogeneous Reactions

Write the equilibrium-constant expression K_c for

SOLUTION

Analyze We are given two chemical equations, both for heterogeneous equilibria, and asked to write the corresponding equilibrium-constant expressions.

Plan We use the law of mass action, remembering to omit any pure solids and pure liquids from the expressions.

Solve

(a) The equilibrium-constant expression is

Because H₂O appears in the reaction as a liquid, its concentration does not appear in the equilibrium-constant expression.

(b) The equilibrium-constant expression is

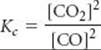
Because SnO₂ and Sn are pure solids, their concentrations do not appear in the equilibrium-constant expression.

PRACTICE EXERCISE

Write the following equilibrium-constant expressions:

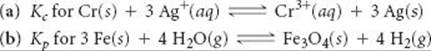
Answers:

SAMPLE EXERCISE 15.7 Analyzing a Heterogeneous Equilibrium

Each of these mixtures was placed in a closed container and allowed to stand:

Determine whether or not each mixture can attain the equilibrium

SOLUTION

Analyze We are asked which of several combinations of species can establish an equilibrium between calcium carbonate and its decomposition products, calcium oxide and carbon dioxide.

Plan For equilibrium to be achieved, it must be possible for both the forward process and the reverse process to occur. For the forward process to occur, there must be some calcium carbonate present. For the reverse process to occur, there must be both calcium oxide and carbon dioxide. In both cases, either the necessary compounds may be present initially or they may be formed by reaction of the other species.

Solve Equilibrium can be reached in all cases except (c) as long as sufficient quantities of solids are present. (a) CaCO₃ simply decomposes, forming CaO(s) and CO₂(g) until the equilibrium pressure of CO₂ is attained. There must be enough CaCO₃, however, to allow the CO₂ pressure to reach equilibrium. (b) CO₂ continues to combine with CaO until the partial pressure of the CO₂ decreases to the equilibrium value. (c) There is no CaO present, so equilibrium cannot be attained because there is no way the CO₂ pressure can decrease to its equilibrium value (which would require some of the CO₂ to react with CaO). (d) The situation is essentially the same as in (a): CaCO₃ decomposes until equilibrium is attained. The presence of CaO initially makes no difference.

PRACTICE EXERCISE

When added to Fe₃O₄(s) in a closed container, which one of the following substances — H₂(g), H₂O(g), O₂(g) — allows equilibrium to be established in the reaction 3 Fe(s) + 4 H₂O(g) Fe₃O₄(s) + 4 H₂(g)?

Answer: H₂(g)

When a solvent is a reactant or product in an equilibrium, its concentration is omitted from the equilibrium-constant expression, provided the concentrations of reactants and products are low, so that the solvent is essentially a pure substance. Applying this guideline to an equilibrium involving water as a solvent,

gives an equilibrium-constant expression that does not contain [H₂O]:

GIVE IT SOME THOUGHT

Write the equilibrium-constant expression for the reaction NH₃(aq) + H₂O(l) NH₄⁺(aq) + OH^–(aq)