CHEMISTRY THE CENTRAL SCIENCE

15 CHEMICAL EQUILIBRIUM

15.5 CALCULATING EQUILIBRIUM CONSTANTS

If we can measure the equilibrium concentrations of all the reactants and products in a chemical reaction, as we did with the data in Table 15.1, calculating the value of the equilibrium constant is straightforward. We simply insert all the equilibrium concentrations into the equilibrium-constant expression for the reaction.

SAMPLE EXERCISE 15.8 Calculating K When All Equilibrium Concentrations Are Known

After a mixture of hydrogen and nitrogen gases in a reaction vessel is allowed to attain equilibrium at 472 °C, it is found to contain 7.38 atm H₂, 2.46 atm N₂, and 0.166 atm NH₃. From these data, calculate the equilibrium constant K_p for the reaction

SOLUTION

Analyze We are given a balanced equation and equilibrium partial pressures and are asked to calculate the value of the equilibrium constant.

Plan Using the balanced equation, we write the equilibrium-constant expression. We then substitute the equilibrium partial pressures into the expression and solve for K_p.

Solve

PRACTICE EXERCISE

An aqueous solution of acetic acid is found to have the following equilibrium concentrations at 25 °C: [CH₃COOH] = 1.65 × 10^–2M; [H+] = 5.44 × 10^–4M; and [CH₃COO-] = 5.44 × 10^–4M. Calculate the equilibrium constant K_c for the ionization of acetic acid at 25 °C. The reaction is

Answer: 1.79 × 10^–5

Often we do not know the equilibrium concentrations of all species in an equilibrium mixture. If we know the equilibrium concentration of at least one species, however, we can generally use the stoichiometry of the reaction to deduce the equilibrium concentrations of the others. The following steps outline the procedure:

1. Tabulate all known initial and equilibrium concentrations of the species that appear in the equilibrium-constant expression.

2. For those species for which initial and equilibrium concentrations are known, calculate the change in concentration that occurs as the system reaches equilibrium.

3. Use the stoichiometry of the reaction (that is, the coefficients in the balanced chemical equation) to calculate the changes in concentration for all other species in the equilibrium-constant expression.

4. Use initial concentrations from step 1 and changes in concentration from step 3 to calculate any equilibrium concentrations not tabulated in step 1.

5. Determine the value of the equilibrium constant.

SAMPLE EXERCISE 15.9 Calculating K from Initial and Equilibrium Concentrations

A closed system initially containing 1.000 × 10^–3M H₂ and 2.000 × 10^–3M I₂ at 448 °C is allowed to reach equilibrium, and at equilibrium the HI concentration is 1.87 × 10^–3M. Calculate K_c at 448 °C for the reaction taking place, which is

SOLUTION

Analyze We are given the initial concentrations of H₂ and l₂ and the equilibrium concentration of HI. We are asked to calculate the equilibrium constant K_c for H₂(g) + I₂(g) 2 Hl(g).

Plan We construct a table to find equilibrium concentrations of all species and then use the equilibrium concentrations to calculate the equilibrium constant.

Solve First, we tabulate the initial and equilibrium concentrations of as many species as we can. We also provide space in our table for listing the changes in concentrations. As shown, it is convenient to use the chemical equation as the heading for the table.

Second, we calculate the change in HI concentration, which is the difference between the equilibrium and initial values:

Third, we use the coefficients in the balanced equation to relate the change in [HI] to the changes in [H₂] and [I₂]:

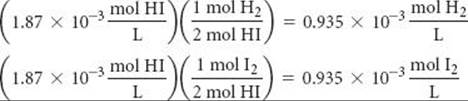
Fourth, we calculate the equilibrium concentrations of H₂ and I₂, using initial concentrations and changes in concentration. The equilibrium concentration equals the initial concentration minus that consumed:

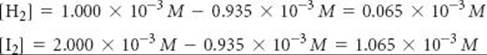
Our table now looks like this (with equilibrium concentrations in blue for emphasis):

Notice that the entries for the changes are negative when a reactant is consumed and positive when a product is formed.

Finally, we use the equilibrium-constant expression to calculate the equilibrium constant:

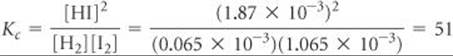
Comment The same method can be applied to gaseous equilibrium problems to calculate K_p, in which case partial pressures are used as table entries in place of molar concentrations. Your instructor may refer to this kind of table as an ICE chart, where ICE stands for Initial – Change –Equilibrium.

PRACTICE EXERCISE

Sulfur trioxide decomposes at high temperature in a sealed container: 2 SO₃(g) 2 SO₂(g) + O₂(g). Initially, the vessel is charged at 1000 K with SO₃(g) at a partial pressure of 0.500 atm. At equilibrium the SO₃ partial pressure is 0.200 atm. Calculate the value of K_p at 1000 K.

Answer: 0.338