CHEMISTRY THE CENTRAL SCIENCE

16 ACID–BASE EQUILIBRIA

16.3 THE AUTOIONIZATION OF WATER

One of the most important chemical properties of water is its ability to act as either a Brønsted–Lowry acid or a Brønsted–Lowry base. In the presence of an acid, it acts as a proton acceptor; in the presence of a base, it acts as a proton donor. In fact, one water molecule can donate a proton to another water molecule:

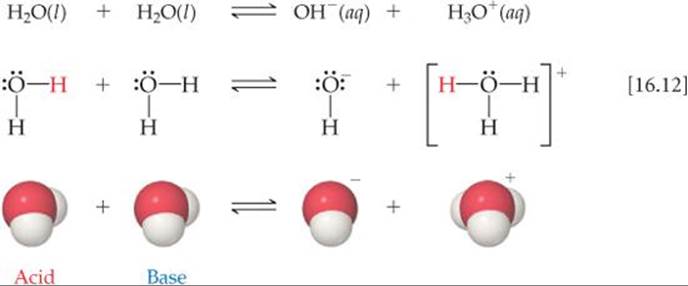
We call this process the autoionization of water.

Because the forward and reverse reactions in Equation 16.12 are extremely rapid no water molecule remains ionized for long. At room temperature only about two out of every 10⁹ water molecules are ionized at any given instant. Thus, pure water consists almost entirely of H₂O molecules and is an extremely poor conductor of electricity. Nevertheless, the autoionization of water is very important, as we will soon see.

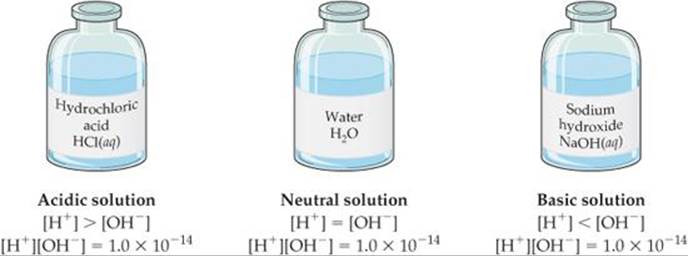
FIGURE 16.4 Relative concentrations of H⁺ and OH^– in aqueous solutions at 25 °C.

The Ion Product of Water

The equilibrium-constant expression for the autoionization of water is

The term [H₂O] is excluded from the equilibrium-constant expression because we exclude the concentrations of pure solids and liquids. (Section 15.4) Because this expression refers specifically to the autoionization of water, we use the symbol K_w to denote the equilibrium constant, which we call the ion-product constant for water. At 25°C, K_w equals 1.0 × 10^–14. Thus, we have

Because we use H⁺(aq) and H₃O⁺(aq) interchangeably to represent the hydrated proton, the autoionization reaction for water can also be written as

Likewise, the expression for K_w can be written in terms of either H₃O⁺ or H⁺, and K_w has the same value in either case:

This equilibrium-constant expression and the value of K_w at 25 °C are extremely important, and you should commit them to memory.

A solution in which [H⁺] = [OH^–] is said to be neutral. In most solutions, however, the H⁺ and OH^– concentrations are not equal. As the concentration of one of these ions increases, the concentration of the other must decrease, so that the product of their concentrations always equals 1.0 × 10^–14 (FIGURE 16.4).

SAMPLE EXERCISE 16.4 Calculating [H⁺] for Pure Water

Calculate the values of [H⁺] and [OH^–] in a neutral solution at 25 °C.

SOLUTION

Analyze We are asked to determine the concentrations of H⁺ and OH^– ions in a neutral solution at 25 °C.

Plan We will use Equation 16.16 and the fact that, by definition, [H⁺] = [OH^–] in a neutral solution.

Solve We will represent the concentration of H⁺ and OH^– in neutral solution with x. This gives

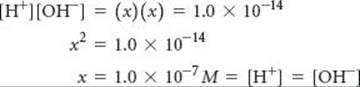
In an acid solution [H⁺] is greater than 1.0×10^–7M; in a basic solution [H⁺] is less than 1.0 × 10^–7M.

PRACTICE EXERCISE

Indicate whether solutions with each of the following ion concentrations are neutral, acidic, or basic: (a) [H⁺] = 4 × 10^–9M; (b) [OH^–] = 1 × 10^–7M; (c) [OH^–] = 7 × 10^–13M.

Answers: (a) basic, (b) neutral, (c) acidic

What makes Equation 16.16 particularly useful is that it is applicable both to pure water and to any aqueous solution. Although the equilibrium between H⁺(aq) and OH^–(aq) as well as other ionic equilibria are affected somewhat by the presence of additional ions in solution, it is customary to ignore these ionic effects except in work requiring exceptional accuracy. Thus, Equation 16.16 is taken to be valid for any dilute aqueous solution and can be used to calculate either [H⁺] (if [OH^–] is known) or [OH^–] (if [H⁺] is known).

SAMPLE EXERCISE 16.5 Calculating [H⁺] from [OH^–]

Calculate the concentration of H⁺(aq) in (a) a solution in which [OH^–] is 0.010 M, (b) a solution in which [OH^–] is 1.8 × 10^–9M. Note: In this problem and all that follow, we assume, unless stated otherwise, that the temperature is 25 °C.

SOLUTION

Analyze We are asked to calculate the [H⁺] concentration in an aqueous solution where the hydroxide concentration is known.

Plan We can use the equilibrium-constant expression for the auto-ionization of water and the value of K_w to solve for each unknown concentration.

Solve

(a) Using Equation 16.16, we have

This solution is basic because

(b) In this instance

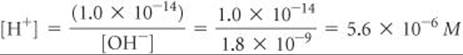
This solution is acidic because

PRACTICE EXERCISE

Calculate the concentration of OH^–(aq) in a solution in which (a) [H⁺] = 2 × 10^–6M;

(b) [H⁺] = [OH^–]; (c) [H⁺] = 100 × [OH^–].

Answers: (a) 5 × 10^–9M, (b) 1.0 × 10^–7M, (c) 1.0 × 10^–8M