CHEMISTRY THE CENTRAL SCIENCE
17 ADDITIONAL ASPECTS OF AQUEOUS EQUILIBRIA
17.2 BUFFERED SOLUTIONS
Solutions that contain a weak conjugate acid–base pair, such as those discussed in Section 17.1, resist drastic changes in pH when small amounts of strong acid or strong base are added to them. These solutions are called buffered solutions (or merely buffers). Human blood, for example, is a complex buffered solution that maintains the blood pH at about 7.4 (see the “Chemistry and Life” box on page 713). Much of the chemical behavior of seawater is determined by its pH, buffered at about 8.1 to 8.3 near the surface (see “Chemistry and Life” box on page 728). Buffered solutions find many important applications in the laboratory and in medicine (
FIGURE 17.1).
FIGURE 17.1 Buffered solutions. For laboratory work, prepackaged buffered solutions can be purchased.
Composition and Action of Buffered Solutions
A buffer resists changes in pH because it contains both an acid to neutralize added OH– ions and a base to neutralize added H+ ions. The acid and base that make up the buffer, however, must not consume each other through a neutralization reaction. These requirements are fulfilled by a weak acid–base conjugate pair, such as CH3COOH–CH3COO– or NH4+–NH3. Thus, buffers are often prepared by mixing a weak acid or a weak base with a salt of that acid or base. The CH3COOH–CH3COO– buffer can be prepared, for example, by adding CH3COONa to a solution of CH3COOH. The NH4+–NH3 buffer can be prepared by adding NH4Cl to a solution of NH3. By choosing appropriate components and adjusting their relative concentrations, we can buffer a solution at virtually any pH.
GIVE IT SOME THOUGHT
Which of these conjugate acid–base pairs will not function as a buffer:
C2H5COOH and C2H5COO–, HCO3– and CO32–, or HNO3 and NO3–? Explain.
To understand how a buffer works, let's consider one composed of a weak acid HX and one of its salts MX, where M+ could be Na+, K+, or any other cation that does not react with water. The acid-dissociation equilibrium in this buffered solution involves both the acid and its conjugate base:
The corresponding acid-dissociation-constant expression is
Solving this expression for [H+], we have
We see from this expression that [H+] and, thus, the pH are determined by two factors: the value of Ka for the weak-acid component of the buffer and the ratio of the concentrations of the conjugate acid–base pair, [HX]/[X–].
If OH– ions are added to the buffered solution, they react with the buffer acid component to produce water and X–:
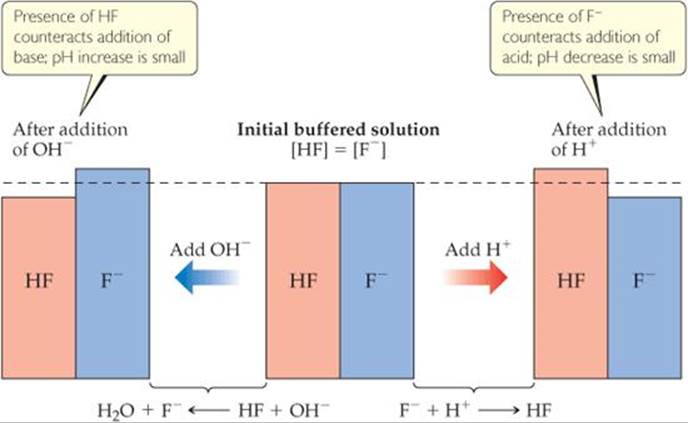
FIGURE 17.2 Buffer action. The pH of an HF/F– buffered solution changes by only a small amount in response to addition of an acid or base.
This reaction causes [HX] to decrease and [X–] to increase. As long as the amounts of HX and X– in the buffer are large relative to the amount of OH– added, the ratio [HX]/[X–] does not change much and, thus, the change in pH is small.
If H+ ions are added, they react with the base component of the buffer:
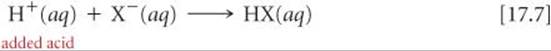
This reaction can also be represented using H3O+:
Using either equation, we see that the reaction causes [X–] to decrease and [HX] to increase. As long as the change in the ratio [HX]/[X–] is small, the change in pH will be small.
FIGURE 17.2 shows an HX/MX buffer consisting of equal concentrations of hydrofluoric acid and fluoride ion (center). The addition of OH– reduces [HF] and increases [F–], whereas the addition of [H+] reduces [F–] and increases [HF].
GIVE IT SOME THOUGHT
a. What happens when NaOH is added to a buffer composed of CH3COOH and CH3COO–?
b. What happens when HCl is added to this buffer?
Calculating the pH of a Buffer
Because conjugate acid–base pairs share a common ion, we can use the same procedures to calculate the pH of a buffer that we used to treat the common-ion effect in Sample Exercise 17.1. Alternatively, we can take an approach based on an equation derived from Equation 17.5. Taking the negative logarithm of both sides of Equation 17.5, we have
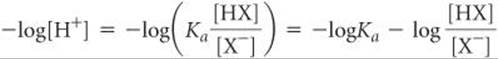
Because –log[H+] = pH and –logKa = pKa, we have
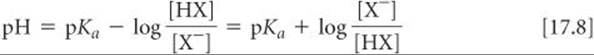
In general,
where [acid] and [base] refer to the equilibrium concentrations of the conjugate acid–base pair. Note that when [base] = [acid], we have pH = pKa.
Equation 17.9 is known as the Henderson–Hasselbalch equation. Biologists, biochemists, and others who work frequently with buffers often use this equation to calculate the pH of buffers. In doing equilibrium calculations, we have seen that we can normally neglect the amounts of the acid and base of the buffer that ionize. Therefore, we can usually use the starting concentrations of the acid and base components of the buffer directly in Equation 17.9.
SAMPLE EXERCISE 17.3 Calculating the pH of a Buffer
What is the pH of a buffer that is 0.12 M in lactic acid [CH3CH(OH)COOH, or HC3H5O3] and 0.10 M in sodium lactate [CH3CH(OH)COONa, or NaC3H5O3]? For lactic acid, Ka = 1.4 × 10–4.
SOLUTION
Analyze We are asked to calculate the pH of a buffer containing lactic acid (HC3H5O3) and its conjugate base, the lactate ion (C3H5O3–).
Plan We will first determine the pH using the method described in Section 17.1. Because HC3H5O3 is a weak electrolyte and NaC3H5O3 is a strong electrolyte, the major species in solution are HC3H5O3, Na+, and C3H5O3–. The Na+ ion is a spectator ion. The HC3H5O3–C3H5O3– conjugate acid–base pair determines [H+] and, thus, pH; [H+] can be determined using the acid-dissociation equilibrium of lactic acid.
Solve The initial and equilibrium concentrations of the species involved in this equilibrium are
The equilibrium concentrations are governed by the equilibrium expression:
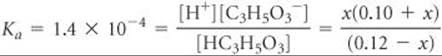
Because Ka is small and a common ion is present, we expect x to be small relative to either 0.12 or 0.10 M. Thus, our equation can be simplified to give
Solving for x gives a value that justifies our approximation:
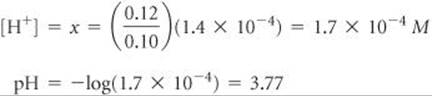
Alternatively, we can use the Henderson–Hasselbalch equation to calculate pH directly:
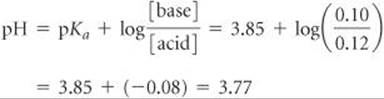
PRACTICE EXERCISE
Calculate the pH of a buffer composed of 0.12 M benzoic acid and 0.20 M sodium benzoate. (Refer to Appendix D.)
Answer: 4.42
In Sample Exercise 17.3 we calculated the pH of a buffered solution. Often we will need to work in the opposite direction by calculating the amounts of the acid and its conjugate base needed to achieve a specific pH. This calculation is illustrated in Sample Exercise 17.4.
SAMPLE EXERCISE 17.4 Preparing a Buffer
How many moles of NH4Cl must be added to 2.0 L of 0.10 M NH3 to form a buffer whose pH is 9.00? (Assume that the addition of NH4Cl does not change the volume of the solution.)
SOLUTION
Analyze We are asked to determine the amount of NH4+ ion required to prepare a buffer of a specific pH.
Plan The major species in the solution will be NH4+, Cl–, and NH3. Of these, the Cl– ion is a spectator (it is the conjugate base of a strong acid). Thus, the NH4+–NH3 conjugate acid–base pair will determine the pH of the buffer. The equilibrium relationship between NH4+ and NH3 is given by the base-dissociation reaction for NH3:
The key to this exercise is to use this Kb expression to calculate [NH4+].
Solve We obtain [OH–] from the given pH:
and so
Because Kb is small and the common ion [NH4+] is present, the equilibrium concentration of NH3 essentially equals its initial concentration:
We now use the expression for Kb to calculate [NH4+]:
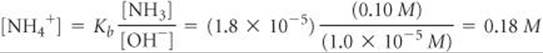
Thus, for the solution to have pH = 9.00, [NH4+] must equal 0.18 M. The number of moles of NH4Cl needed to produce this concentration is given by the product of the volume of the solution and its molarity:
Comment Because NH4+ and NH3 are a conjugate acid–base pair, we could use the Henderson–Hasselbalch equation (Equation 17.9) to solve this problem. To do so requires first using Equation 16.41 to calculate pKa for NH4+ from the value of pKa for NH3. We suggest you try this approach to convince yourself that you can use the Henderson–Hasselbalch equation for buffers for which you are given Kb for the conjugate base rather than Ka for the conjugate acid.
PRACTICE EXERCISE
Calculate the concentration of sodium benzoate that must be present in a 0.20 M solution of benzoic acid (C6H5COOH) to produce a pH of 4.00.
Answer: 0.13 M
Buffer Capacity and pH Range
Two important characteristics of a buffer are its capacity and its effective pH range. Buffer capacity is the amount of acid or base the buffer can neutralize before the pH begins to change to an appreciable degree. The buffer capacity depends on the amount of acid and base used to prepare the buffer. According to Equation 17.5, for example, the pH of a 1-L solution that is 1 M in CH3COOH and 1 M in CH3COONa is the same as the pH of a 1-L solution that is 0.1 M in CH3COOH and 0.1 M in CH3COONa. The first solution has a greater buffering capacity, however, because it contains more CH3COOH and CH3COO–.
The pH range of any buffer is the pH range over which the buffer acts effectively. Buffers most effectively resist a change in pH in either direction when the concentrations of weak acid and conjugate base are about the same. From Equation 17.9 we see that when the concentrations of weak acid and conjugate base are equal, pH = pKa. This relationship gives the optimal pH of any buffer. Thus, we usually try to select a buffer whose acid form has a pKa close to the desired pH. In practice, we find that if the concentration of one component of the buffer is more than 10 times the concentration of the other component, the buffering action is poor. Because log 10 = 1, buffers usually have a usable range within ±1 pH unit of pKa (that is, a range of pH = pKa ± 1).
GIVE IT SOME THOUGHT
The Ka values for nitrous acid (HNO2) and hypochlorous (HClO) acid are 4.5 × 10–4 and 3.0 × 10–8, respectively. Which one would be more suitable for use in a solution buffered at pH = 7.0? What other substance would be needed to make the buffer?
Addition of Strong Acids or Bases to Buffers
Let's now consider in a more quantitative way how a buffered solution responds to addition of a strong acid or base. In this discussion, it is important to understand that reactions between strong acids and weak bases proceed essentially to completion, as do those between strong bases and weak acids. Thus, as long as we do not exceed the buffering capacity of the buffer, we can assume that the strong acid or strong base is completely consumed by reaction with the buffer.
Consider a buffer that contains a weak acid HX and its conjugate base X–. When a strong acid is added to this buffer, the added H+ is consumed by X– to produce HX; thus, [HX] increases and [X–] decreases. (See Equation 17.7.) Upon addition of a strong base, the added OH– is consumed by HX to produce X–; in this case [HX] decreases and [X–] increases. (See Equation 17.6.) These two situations are summarized in Figure 17.2.
To calculate how the pH of the buffer responds to the addition of a strong acid or a strong base, we follow the strategy outlined in 
FIGURE 17.3:
1. Consider the acid–base neutralization reaction and determine its effect on [HX] and [X–]. This step is a stoichiometry calculation. 
(Section 3.6)
2. Use the calculated values of [HX] and [X–] along with Ka to calculate [H+]. This step is an equilibrium calculation and is most easily done using the Henderson–Hasselbalch equation.
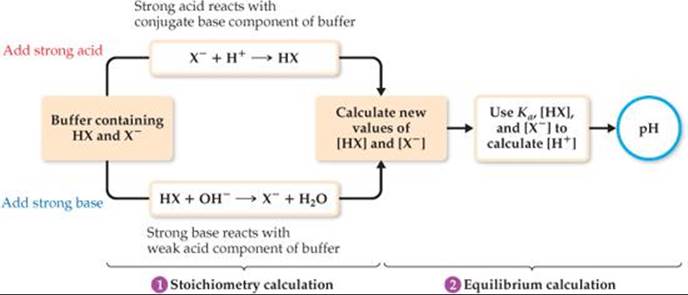
FIGURE 17.3 Calculating the pH of a buffer after addition of an acid or base.
SAMPLE EXERCISE 17.5 Calculating pH Changes in Buffers
A buffer is made by adding 0.300 mol CH3COOH and 0.300 mol CH3COONa to enough water to make 1.000 L of solution. The pH of the buffer is 4.74 (Sample Exercise 17.1). (a) Calculate the pH of this solution after 5.0 mL of 4.0 M NaOH(aq) solution is added. (b) For comparison, calculate the pH of a solution made by adding 5.0 mL of 4.0 M NaOH(aq) solution to 1.000 L of pure water.
SOLUTION
Analyze We are asked to determine the pH of a buffer after addition of a small amount of strong base and to compare the pH change with the pH that would result if we were to add the same amount of strong base to pure water.
Plan Solving this problem involves the two steps outlined in Figure 17.3. First we do a stoi-chiometry calculation to determine how the added OH– affects the buffer composition. Then we use the resultant buffer composition and either the Henderson–Hasselbalch equation or the equilibrium-constant expression for the buffer to determine the pH.
Solve (a) Stoichiometry Calculation: The OH– provided by NaOH reacts with CH3COOH, the weak acid component of the buffer. Prior to this neutralization reaction, there are 0.300 mol each of CH3COOH and CH3COO–. The amount of base added is 0.0050 L × 4.0 mol/L = 0.020 mol. Neutralizing the 0.020 mol OH– requires 0.020 mol of CH3COOH. Consequently, the amount of CH3COOH decreases by 0.020 mol, and the amount of the product of the neutralization, CH3COO–, increases by 0.020 mol. We can create a table to see how the composition of the buffer changes as a result of its reaction with OH–:
Equilibrium Calculation: We now turn our attention to the equilibrium for the ionization of acetic acid, the relationship that determines the buffer pH:
Using the quantities of CH3COOH and CH3COO– remaining in the buffer, we determine the pH using the Henderson–Hasselbalch equation. The volume of the solution is now 1.000 L + 0.0050 L = 1.005 L due to addition of the NaOH solution:
(b) To determine the pH of a solution made by adding 0.020 mol of NaOH to 1.000 L of pure water, we first determine the concentration of OH– ions in solution,
[OH–] = 0.020 mol/(1.005 L) = 0.020 M
We use this value in Equation 16.18 to calculate pOH and then use our calculated pOH value in Equation 16.20 to obtain pH:
Comment Note that the small amount of added NaOH changes the pH of water significantly. In contrast, the pH of the buffer changes very little when the NaOH is added, as summarized in 
FIGURE 17.4.
FIGURE 17.4 Effect of adding a strong base to a buffered solution and to water.
PRACTICE EXERCISE
Determine (a) the pH of the original buffer described in Sample Exercise 17.5 after the addition of 0.020 mol HCl and (b) the pH of the solution that would result from the addition of 0.020 mol HCl to 1.000 L of pure water.
Answers: (a) 4.68, (b) 1.70
CHEMISTRY AND LIFE
BLOOD AS A BUFFERED SOLUTION
Chemical reactions that occur in living systems are often extremely sensitive to pH. Many of the enzymes that catalyze important biochemical reactions, for example, are effective only within a narrow pH range. For this reason, the human body maintains a remarkably intricate system of buffers, both within cells and in the fluids that transport cells. Blood, the fluid that transports oxygen to all parts of the body, is one of the most prominent examples of the importance of buffers in living beings.
Human blood has a normal pH of 7.35 to 7.45. Any deviation from this range can have extremely disruptive effects on the stability of cell membranes, the structures of proteins, and the activities of enzymes. Death may result if the blood pH falls below 6.8 or rises above 7.8. When the pH falls below 7.35, the condition is called acidosis; when it rises above 7.45, the condition is called alkalosis. Acidosis is the more common tendency because metabolism generates several acids in the body.
The major buffer system used to control blood pH is the carbonic acid–bicarbonate buffer system. Carbonic acid (H2CO3) and bicarbonate ion (HCO3–) are a conjugate acid–base pair. In addition, carbonic acid decomposes into carbon dioxide gas and water. The important enuilibria in this buffer system are
Several aspects of these equilibria are notable. First, although carbonic acid is diprotic, the carbonate ion (CO32–) is unimportant in this system. Second, one component of this equilibrium, CO2, is a gas, which provides a mechanism for the body to adjust the equilibria. Removal of CO2via exhalation shifts the equilibria to the right, consuming H+ ions. Third, the buffer system in blood operates at pH 7.4, which is fairly far removed from the pKa1 value of H2CO3 (6.1 at physiological temperatures). For the buffer to have a pH of 7.4, the ratio [base]/[acid] must be about 20. In normal blood plasma the concentrations of HCO3– and H2CO3 are about 0.024 M and 0.0012 M, respectively. Consequently, the buffer has a high capacity to neutralize additional acid but only a low capacity to neutralize additional base.
The principal organs that regulate the pH of the carbonic acid–bicarbonate buffer system are the lungs and kidneys. When the concentration of CO2 rises, the equilibria in Equation 17.10 shift to the left, which leads to the formation of more H+ and a drop in pH. This change is detected by receptors in the brain that trigger a reflex to breathe faster and deeper, increasing the rate at which CO2 is expelled from the lungs and thereby shifting the equilibria back to the right. When the blood pH becomes too high, the kidneys remove HCO3– from the blood. This shifts the equilibria to the left, increasing the concentration of H+. As a result, the pH decreases.
Regulation of blood pH relates directly to the effective transport of O2 throughout the body. The protein hemoglobin, found in red blood cells (
FIGURE 17.5), carries oxygen. Hemoglobin (Hb) reversibly binds both H+ and O2. these two substances compete for the Hb, which can be represented approximately by the equilibrium
Oxygen enters the blood through the lungs, where it passes into the red blood cells and binds to Hb. When the blood reaches tissue in which the concentration of O2 is low, the equilibrium in Equation 17.11 shifts to the left and O2 is released.
During periods of strenuous exertion, three factors work together to ensure delivery of O2 to active tissues. The role of each factor can be understood by applying Le Châtelier's principle to Equation 17.11:
1. O2 is consumed, causing the equilibrium to shift to the left, releasing more O2.
2. Large amounts of CO2 are produced by metabolism, which increases [H+] and causes the equilibrium to shift to the left, releasing O2.
3. Body temperature rises. Because Equation 17.11 is exothermic, the increase in temperature shifts the equilibrium to the left, releasing O2.
In addition to the factors causing release of O2 to tissues, the decrease in pH stimulates an increase in breathing rate, which furnishes more O2 and eliminates CO2. Without this elaborate series of equilibrium shifts and pH changes, the O2 in tissues would be rapidly depleted, making further activity impossible. Under such conditions the buffering capacity of the blood and the exhalation of CO2 through the lungs are essential to keep the pH from dropping too low, thereby triggering acidosis.
RELATED EXERCISES: 17.29 and 17.95
FIGURE 17.5 Red blood cells. A scanning electromicrograph of red blood cells traveling through a small branch of an artery.