CHEMISTRY THE CENTRAL SCIENCE
17 ADDITIONAL ASPECTS OF AQUEOUS EQUILIBRIA
17.3 ACID–BASE TITRATIONS
In an acid–base titration, a solution containing a known concentration of base is slowly added to an acid (or the acid is added to the base). ![]() (Section 4.6) Acid–base indicators can be used to signal the equivalence point of a titration (the point at which stoichiometrically equivalent quantities of acid and base have been brought together). Alternatively, a pH meter can be used to monitor the progress of the reaction (
(Section 4.6) Acid–base indicators can be used to signal the equivalence point of a titration (the point at which stoichiometrically equivalent quantities of acid and base have been brought together). Alternatively, a pH meter can be used to monitor the progress of the reaction (![]() FIGURE 17.6), producing a pH titration curve, a graph of the pH as a function of the volume of titrant added. The shape of the titration curve makes it possible to determine the equivalence point. The curve can also be used to select suitable indicators and to determine the Ka of the weak acid or the Kb of the weak base being titrated.
FIGURE 17.6), producing a pH titration curve, a graph of the pH as a function of the volume of titrant added. The shape of the titration curve makes it possible to determine the equivalence point. The curve can also be used to select suitable indicators and to determine the Ka of the weak acid or the Kb of the weak base being titrated.
![]() GO FIGURE
GO FIGURE
In which direction do you expect the pH to change as NaOH is added to the HCl solution?
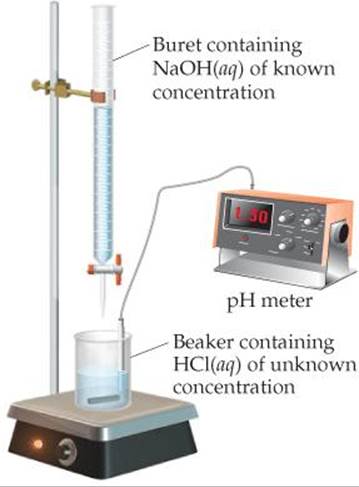
![]() FIGURE 17.6 Measuring pH during a titration.
FIGURE 17.6 Measuring pH during a titration.
To understand why titration curves have certain characteristic shapes, we will examine the curves for three kinds of titrations: (1) strong acid–strong base, (2) weak acid–strong base, and (3) polyprotic acid–strong base. We will also briefly consider how these curves relate to those involving weak bases.
Strong Acid–Strong Base Titrations
The titration curve produced when a strong base is added to a strong acid has the general shape shown in ![]() FIGURE 17.7, which depicts the pH change that occurs as 0.100 M NaOH is added to 50.0 mL of 0.100 M HCl. The pH can be calculated at various stages of the titration. To help understand these calculations, we can divide the curve into four regions:
FIGURE 17.7, which depicts the pH change that occurs as 0.100 M NaOH is added to 50.0 mL of 0.100 M HCl. The pH can be calculated at various stages of the titration. To help understand these calculations, we can divide the curve into four regions:
![]() GO FIGURE
GO FIGURE
What volume of NaOH(aq) would be needed to reach the equivalence point if the concentration of the added base were 0.200 M?
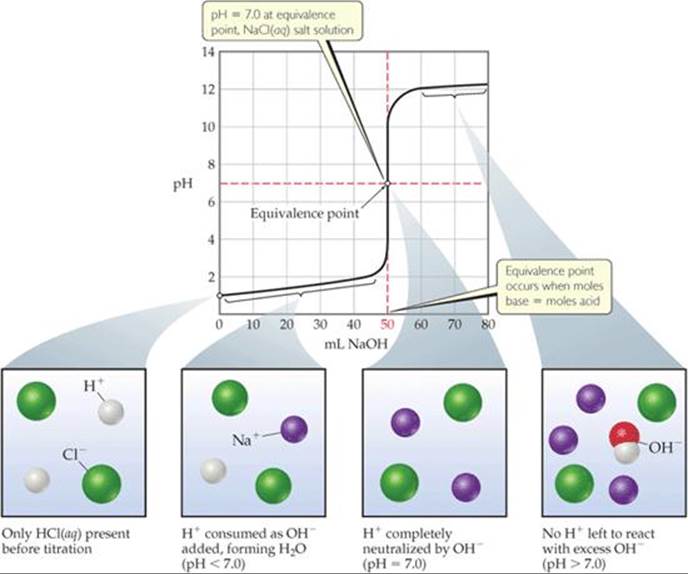
![]() FIGURE 17.7 Titration of a strong acid with a strong base. The pH curve for titration of 50.0 mL of a 0.100 M solution of hydrochloric acid with a 0.100 M solution of NaOH(aq). For clarity, water molecules have been omitted from the molecular art.
FIGURE 17.7 Titration of a strong acid with a strong base. The pH curve for titration of 50.0 mL of a 0.100 M solution of hydrochloric acid with a 0.100 M solution of NaOH(aq). For clarity, water molecules have been omitted from the molecular art.
1. Initial pH: The pH of the solution before the addition of any base is determined by the initial concentration of the strong acid. For a solution of 0.100 M HCl, [H+] = 0.100 M and pH = –log(0.100) = 1.000. Thus, the initial pH is low.
2. Between initial pH and equivalence point: As NaOH is added, the pH increases slowly at first and then rapidly in the vicinity of the equivalence point. The pH before the equivalence point is determined by the concentration of acid not yet neutralized. This calculation is illustrated in Sample Exercise 17.6(a).
3. Equivalence point: At the equivalence point an equal number of moles of NaOH and HCl have reacted, leaving only a solution of their salt, NaCl. The pH of the solution is 7.00 because the cation of a strong base (in this case Na+) and the anion of a strong acid (in this case Cl–) are neither acids nor bases and, therefore, have no appreciable effect on pH. ![]() (Section 16.9)
(Section 16.9)
4. After equivalence point: The pH of the solution after the equivalence point is determined by the concentration of excess NaOH in the solution. This calculation is illustrated in Sample Exercise 17.6(b).
SAMPLE EXERCISE 17.6 Calculating pH for a Strong Acid–Strong Base Titration
Calculate the pH when (a) 49.0 mL and (b) 51.0 mL of 0.100 M NaOH solution have been added to 50.0 mL of 0.100 M HCl solution.
SOLUTION
Analyze We are asked to calculate the pH at two points in the titration of a strong acid with a strong base. The first point is just before the equivalence point, so we expect the pH to be determined by the small amount of strong acid that has not yet been neutralized. The second point is just after the equivalence point, so we expect this pH to be determined by the small amount of excess strong base.
Plan (a) As the NaOH solution is added to the HCl solution, H+(aq) reacts with OH–(aq) to form H2O. Both Na+ and Cl– are spectator ions, having negligible effect on the pH. To determine the pH of the solution, we must first determine how many moles of H+ were originally present and how many moles of OH– were added. We can then calculate how many moles of each ion remain after the neutralization reaction. To calculate [H+], and hence pH, we must also remember that the volume of the solution increases as we add titrant, thus diluting the concentration of all solutes present
Solve The number of moles of H+ in the original HCl solution is given by the product of the volume of the solution and its molarity:
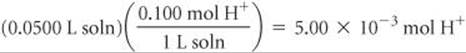
Likewise, the number of moles of OH– in 49.0 mL of 0.100 M NaOH is
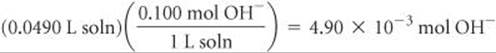
Because we have not reached the equivalence point, there are more moles of H+ present than OH–. Each mole of OH– reacts with 1 mol of H+. Using the convention introduced in Sample Exercise 17.5, we have

The volume of the reaction mixture increases as the NaOH solution is added to the HCl solution. Thus, at this point in the titration, the volume in the titration flask is
![]()
Thus, the concentration of H+(aq) in the flask is
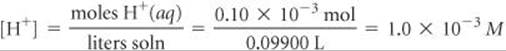
The corresponding pH is
![]()
Plan (b) We proceed in the same way as we did in part (a) except we are now past the equivalence point and have more OH– in the solution than H+. As before, the initial number of moles of each reactant is determined from their volumes and concentrations. The reactant present in smaller stoichiometric amount (the limiting reactant) is consumed completely, leaving an excess of hydroxide ion.
Solve

In this case the volume in the titration flask is
![]()
Hence, the concentration of OH–(aq) in the flask is
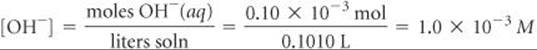
and we have
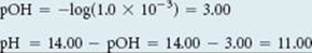
Comment Note that the pH increased by only two pH units, from 1.00 (Figure 17.7) to 3.00, after the first 49.0 mL of NaOH solution was added, but jumped by eight pH units, from 3.00 to 11.00, as 2.0 mL of base solution was added near the equivalence point. Such a rapid rise in pH near the equivalence point is a characteristic of titrations involving strong acids and strong bases.
PRACTICE EXERCISE
Calculate the pH when (a) 24.9 mL and (b) 25.1 mL of 0.100 M HNO3 have been added to 25.0 mL of 0.100 M KOH solution.
Answers: (a) 10.30, (b) 3.70
Titration of a solution of a strong base with a solution of a strong acid yields an analogous curve of pH versus added acid. In this case, however, the pH is high at the outset of the titration and low at its completion (![]() FIGURE 17.8).
FIGURE 17.8).
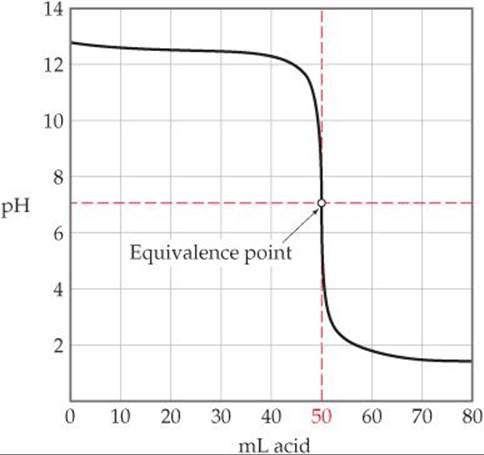
![]() FIGURE 17.8 Titration of a strong base with a strong acid. The pH curve for titration of 50.0 mL of a 0.100 M solution of a strong base with a 0.100 M solution of a strong acid.
FIGURE 17.8 Titration of a strong base with a strong acid. The pH curve for titration of 50.0 mL of a 0.100 M solution of a strong base with a 0.100 M solution of a strong acid.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
What is the pH at the equivalence point when 0.10 M HNO3 is used to titrate a volume of solution containing 0.30 g of KOH?
Weak Acid–Strong Base Titrations
The curve for titration of a weak acid by a strong base is similar to the curve in Figure 17.7. Consider, for example, the curve for titration of 50.0 mL of 0.100 M acetic acid with 0.100 M NaOH shown in ![]() FIGURE 17.9. We can calculate the pH at points along this curve, using principles we discussed earlier, which means again dividing the curve into four regions:
FIGURE 17.9. We can calculate the pH at points along this curve, using principles we discussed earlier, which means again dividing the curve into four regions:
1. Initial pH: We use Ka to calculate this pH, as shown in Section 16.6. The calculated pH of 0.100 M CH3COOH is 2.89.
2. Between initial pH and equivalence point: Prior to reaching the equivalence point, the acid is being neutralized, and its conjugate base is being formed:
![]()
Thus, the solution contains a mixture of CH3COOH and CH3COO–. Calculating the pH in this region involves two steps. First, we consider the neutralization reaction between CH3COOH and OH– to determine [CH3COOH] and [CH3COO–]. Next, we calculate the pH of this buffer pair using procedures developed in Sections 17.1 and 17.2. The general procedure is diagrammed in ![]() FIGURE 17.10 and illustrated in Sample Exercise 17.7.
FIGURE 17.10 and illustrated in Sample Exercise 17.7.
![]() GO FIGURE
GO FIGURE
If the acetic acid being titrated here were replaced by hydrochloric acid, would the amount of base needed to reach the equivalence point change? Would the pH at the equivalence point change?
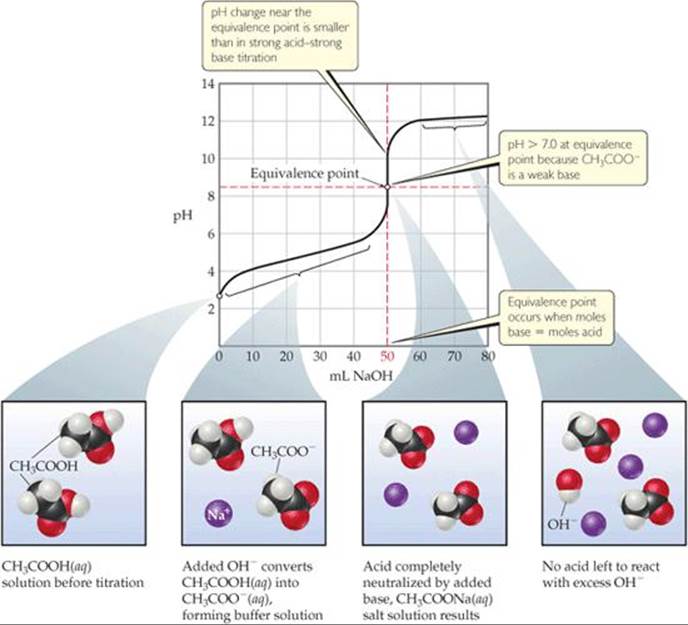
![]() FIGURE 17.9 Titration of a weak acid with a strong base. The pH curve for titration of 50.0 mL of a 0.100 M solution of acetic acid with a 0.100 M solution of NaOH(aq). For clarity, water molecules have been omitted from the molecular art.
FIGURE 17.9 Titration of a weak acid with a strong base. The pH curve for titration of 50.0 mL of a 0.100 M solution of acetic acid with a 0.100 M solution of NaOH(aq). For clarity, water molecules have been omitted from the molecular art.
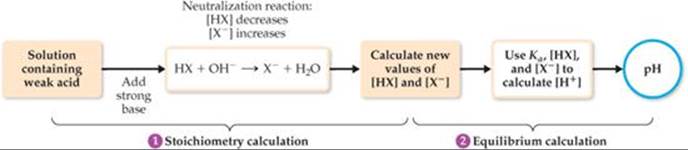
![]() FIGURE 17.10 Procedure for calculating pH when a weak acid is partially neutralized by a strong base.
FIGURE 17.10 Procedure for calculating pH when a weak acid is partially neutralized by a strong base.
3. Equivalence point: The equivalence point is reached when 50.0 mL of 0.100 M NaOH has been added to the 50.0 mL of 0.100 M CH3COOH. At this point, the 5.00 × 10–3 mol of NaOH completely reacts with the 5.00 × 10–3 mol of CH3COOH to form 5.00 × 10–3 mol of CH3COONa. The Na+ ion of this salt has no significant effect on the pH. The CH3COO– ion, however, is a weak base, and the pH at the equivalence point is therefore greater than 7. In general, the pH at the equivalence point is always above 7 in a weak acid–strong base titration because the anion of the salt formed is a weak base. The procedure for calculating the pH of the solution of a weak base is described in Section 16.7 and is shown in Sample Exercise 17.8.
4. After equivalence point (excess base): In this region, [OH–] from the reaction of CH3COO– with water is negligible relative to [OH–] from the excess NaOH. Thus, the pH is determined by the concentration of OH– from the excess NaOH. The method for calculating pH in this region is therefore like that illustrated in Sample Exercise 17.6(b). Thus, the addition of 51.0 mL of 0.100 M NaOH to 50.0 mL of either 0.100 M HCl or 0.100 M CH3COOH yields the same pH, 11.00. Notice by comparing Figures 17.7 and 17.9 that the titration curves for a strong acid and a weak acid are the same after the equivalence point.
SAMPLE EXERCISE 17.7 Calculating pH for a Weak Acid–Strong Base Titration
Calculate the pH of the solution formed when 45.0 mL of 0.100 M NaOH is added to 50.0 mL of 0.100 M CH3COOH (Ka = 1.8 × 10–5).
SOLUTION
Analyze We are asked to calculate the pH before the equivalence point of the titration of a weak acid with a strong base.
Plan We first must determine the number of moles of CH3COOH and CH3COO– present after the neutralization reaction. We then calculate pH using Ka, [CH3COOH], and [CH3COO–].
Solve Stoichiometry Calculation: The product of the volume and concentration of each solution gives the number of moles of each reactant present before the neutralization:
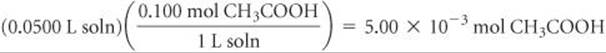
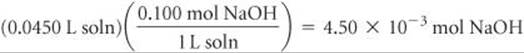
The 4.50 × 10–3 of NaOH consumes 4.50 × 10–3 of CH3COOH:

The total volume of the solution is
![]()
The resulting molarities of CH3COOH and CH3COO– after the reaction are therefore
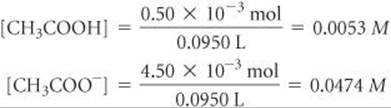
Equilibrium Calculation: The equilibrium between CH3COOH and CH3COO– must obey the equilibrium-constant expression for CH3COOH:
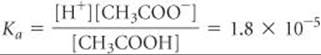
Solving for [H+] gives
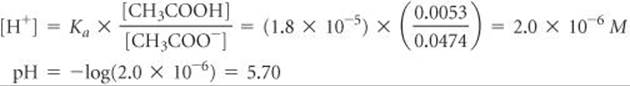
Comment We could have solved for pH equally well using the Henderson–Hasselbalch equation.
PRACTICE EXERCISE
(a) Calculate the pH in the solution formed by adding 10.0 mL of 0.050 M NaOH to 40.0 mL of 0.0250 M benzoic acid (C6H5COOH, Ka = 6.3 × 10–5. (b) Calculate the pH in the solution formed by adding 10.0 mL of 0.100 M HCl to 20.0 mL of 0.100 M NH3.
Answers: (a) 4.20, (b) 9.26
In order to follow the evolution of pH as a function of added base further, we can calculate the pH at the equivalence point.
SAMPLE EXERCISE 17.8 Calculating the pH at the Equivalence Point
Calculate the pH at the equivalence point in the titration of 50.0 mL of 0.100 M CH3COOH with 0.100 M NaOH.
SOLUTION
Analyze We are asked to determine the pH at the equivalence point of the titration of a weak acid with a strong base. Because the neutralization of a weak acid produces its anion, which is a weak base, we expect the pH at the equivalence point to be greater than 7.
Plan The initial number of moles of acetic acid equals the number of moles of acetate ion at the equivalence point. We use the volume of the solution at the equivalence point to calculate the concentration of acetate ion. Because the acetate ion is a weak base, we can calculate the pH usingKb and [CH3COO–].
Solve The number of moles of acetic acid in the initial solution is obtained from the volume and molarity of the solution:
![]()
Hence, 5.00 × 10–3 mol of [CH3COO–] is formed. It will take 50.0 mL of NaOH to reach the equivalence point (Figure 17.9). The volume of this salt solution at the equivalence point is the sum of the volumes of the acid and base, 50.0 mL + 50.0 mL = 100.0 mL = 0.1000 L. Thus, the concentration of CH3COO– is
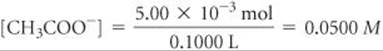
The CH3COO– ion is a weak base:
![]()
The Kb for CH3COO– can be calculated from the Ka value of its conjugate acid, Kb = Kw/Ka = (1.0 × 10–14)/(1.8 × 10–5) = 5.6 × 10–10. Using the Kb expression, we have
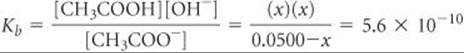
Making the approximation that 0.0500 – x ![]() 0.0500, and then solving for x, we have x = [OH–] = 5.3 × 10–6M, which gives pOH = 5.28 and pH = 8.72.
0.0500, and then solving for x, we have x = [OH–] = 5.3 × 10–6M, which gives pOH = 5.28 and pH = 8.72.
Check The pH is above 7, as expected for the salt of a weak acid and strong base.
PRACTICE EXERCISE
Calculate the pH at the equivalence point when (a) 40.0 mL of 0.025 M benzoic acid (C6H5COOH, Ka = 6.3 × 10–5) is titrated with 0.050 M NaOH; (b) 40.0 mL of 0.100 M NH3 is titrated with 0.100 M HCl.
Answers: (a) 8.21, (b) 5.28
The titration curve for a weak acid–strong base titration (Figure 17.9) differs from the curve for a strong acid–strong base titration (Figure 17.7) in three noteworthy ways:
1. The solution of the weak acid has a higher initial pH than a solution of a strong acid of the same concentration.
2. The pH change in the rapid-rise portion of the curve near the equivalence point is smaller for the weak acid than for the strong acid.
3. The pH at the equivalence point is above 7.00 for the weak acid titration.
The weaker the acid, the more pronounced these differences become. To illustrate this consider the family of titration curves shown in ![]() FIGURE 17.11. Notice that as the acid becomes weaker (that is, as Ka becomes smaller), the initial pH increases and the pH change near the equivalence point becomes less marked. Furthermore, the pH at the equivalence point steadily increases as Ka decreases, because the strength of the conjugate base of the weak acid increases. It is virtually impossible to determine the equivalence point when pKa is 10 or higher because the pH change is too small and gradual.
FIGURE 17.11. Notice that as the acid becomes weaker (that is, as Ka becomes smaller), the initial pH increases and the pH change near the equivalence point becomes less marked. Furthermore, the pH at the equivalence point steadily increases as Ka decreases, because the strength of the conjugate base of the weak acid increases. It is virtually impossible to determine the equivalence point when pKa is 10 or higher because the pH change is too small and gradual.
![]() GO FIGURE
GO FIGURE
How does the pH at the equivalence point change as the acid being titrated becomes weaker? How does the volume of NaOH(aq) needed to reach the equivalence point change?
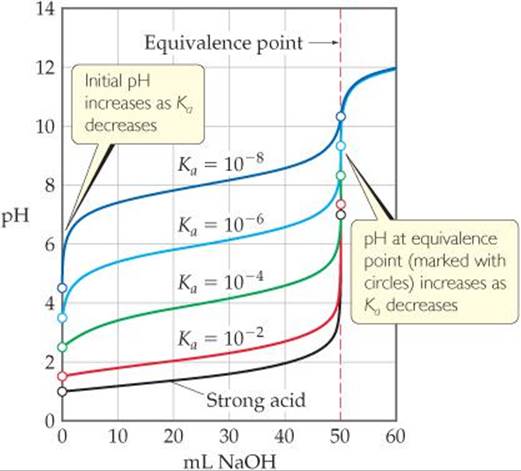
![]() FIGURE 17.11 A set of curves showing the effect of acid strength on the characteristics of the titration curve when a weak acid is titrated by a strong base. Each curve represents titration of 50.0 mL of 0.10 M acid with 0.10 M NaOH.
FIGURE 17.11 A set of curves showing the effect of acid strength on the characteristics of the titration curve when a weak acid is titrated by a strong base. Each curve represents titration of 50.0 mL of 0.10 M acid with 0.10 M NaOH.
Titrations of Polyprotic Acids
When weak acids contain more than one ionizable H atom, the reaction with OH– occurs in a series of steps. Neutralization of H3PO3, for example, proceeds in two steps (Chapter 16 Sample Integrative Exercise):
![]()
![]()
When the neutralization steps of a polyprotic acid or polybasic base are sufficiently separated, the titration has multiple equivalence points. ![]() FIGURE 17.12 shows the two equivalence points corresponding to Equations 17.13 and 17.14.
FIGURE 17.12 shows the two equivalence points corresponding to Equations 17.13 and 17.14.
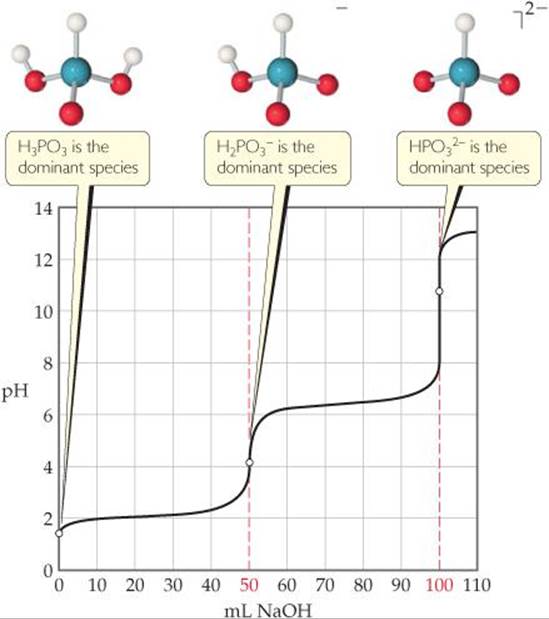
![]() FIGURE 17.12 Titration curve for a diprotic acid. The curve shows the pH change when 50.0 mL of 0.10 M H3PO3 is titrated with 0.10 M NaOH.
FIGURE 17.12 Titration curve for a diprotic acid. The curve shows the pH change when 50.0 mL of 0.10 M H3PO3 is titrated with 0.10 M NaOH.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Sketch an approximate titration curve for the titration of Na2CO3 with HCl.
Titrating with an Acid–Base Indicator
Oftentimes in an acid–base titration, an indicator is used rather than a pH meter. Optimally, an indicator should change color at the equivalence point in a titration. In practice, however, that is unnecessary. The pH changes very rapidly near the equivalence point, and in this region one drop of titrant can change the pH by several units. Thus, an indicator beginning and ending its color change anywhere on the rapid-rise portion of the titration curve gives a sufficiently accurate measure of the titrant volume needed to reach the equivalence point. The point in a titration where the indicator changes color is called the end point to distinguish it from the equivalence point that it closely approximates.
![]() FIGURE 17.13 shows the curve for titration of a strong base (NaOH) with a strong acid (HCl). We see from the vertical part of the curve that the pH changes rapidly from roughly 11 to 3 near the equivalence point. Consequently, an indicator for this titration can change color anywhere in this range. Most strong acid–strong base titrations are carried out using phe-nolphthalein as an indicator because it changes color in this range (see Figure 16.8, page 664). Several other indicators would also be satisfactory, including methyl red, which, as the lower color band inFigure 17.13 shows, changes color in the pH range from about 4.2 to 6.0. (see Figure 16.8, page 664).
FIGURE 17.13 shows the curve for titration of a strong base (NaOH) with a strong acid (HCl). We see from the vertical part of the curve that the pH changes rapidly from roughly 11 to 3 near the equivalence point. Consequently, an indicator for this titration can change color anywhere in this range. Most strong acid–strong base titrations are carried out using phe-nolphthalein as an indicator because it changes color in this range (see Figure 16.8, page 664). Several other indicators would also be satisfactory, including methyl red, which, as the lower color band inFigure 17.13 shows, changes color in the pH range from about 4.2 to 6.0. (see Figure 16.8, page 664).
![]() GO FIGURE
GO FIGURE
Is methyl red a suitable indicator when you are titrating a strong acid with a strong base? Explain your answer.

![]() FIGURE 17.13 Using color indicators for titration of a strong base with a strong acid. Both phenolphthalein and methyl red change color in the rapid-rise portion of the titration curve.
FIGURE 17.13 Using color indicators for titration of a strong base with a strong acid. Both phenolphthalein and methyl red change color in the rapid-rise portion of the titration curve.
As noted in our discussion of Figure 17.11, because the pH change near the equivalence point becomes smaller as Ka decreases, the choice of indicator for a weak acid–strong base titration is more critical than it is for titrations where both acid and base are strong. When 0.100 MCH3COOH (Ka = 1.8 × 10–5) is titrated with 0.100 M NaOH, for example, the pH increases rapidly only over the pH range from about 7 to 11 (![]() FIGURE 17.14). Phenolphthalein is therefore an ideal indicator because it changes color from pH 8.3 to 10.0, close to the pH at the equivalence point. Methyl red is a poor choice, however, because its color change, from 4.2 to 6.0, begins well before the equivalence point is reached.
FIGURE 17.14). Phenolphthalein is therefore an ideal indicator because it changes color from pH 8.3 to 10.0, close to the pH at the equivalence point. Methyl red is a poor choice, however, because its color change, from 4.2 to 6.0, begins well before the equivalence point is reached.
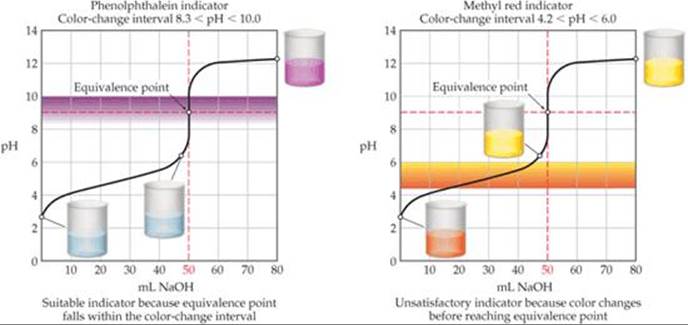
![]() FIGURE 17.14 Good and poor indicators for titration of a weak acid with a strong base.
FIGURE 17.14 Good and poor indicators for titration of a weak acid with a strong base.
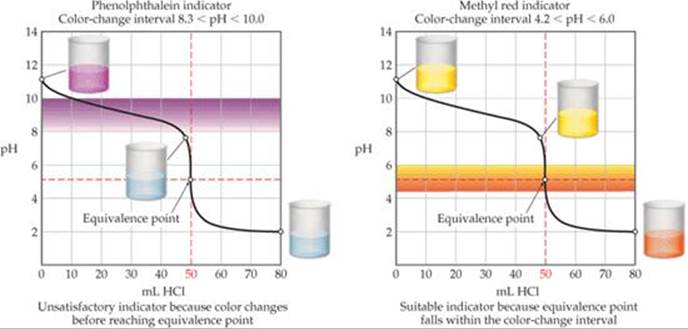
![]() FIGURE 17.15 Good and poor indicators for titration of a weak base with a strong acid.
FIGURE 17.15 Good and poor indicators for titration of a weak base with a strong acid.
Titration of a weak base (such as 0.100 M NH3) with a strong acid solution (such as 0.100 M HCl) leads to the titration curve shown in ![]() FIGURE 17.15. In this example, the equivalence point occurs at pH 5.28. Thus, methyl red is an ideal indicator but phenolphthalein would be a poor choice.
FIGURE 17.15. In this example, the equivalence point occurs at pH 5.28. Thus, methyl red is an ideal indicator but phenolphthalein would be a poor choice.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Why is the choice of indicator more crucial for a weak acid–strong base titration than for a strong acid–strong base titration?