CHEMISTRY THE CENTRAL SCIENCE
17 ADDITIONAL ASPECTS OF AQUEOUS EQUILIBRIA
EXERCISES
VISUALIZING CONCEPTS
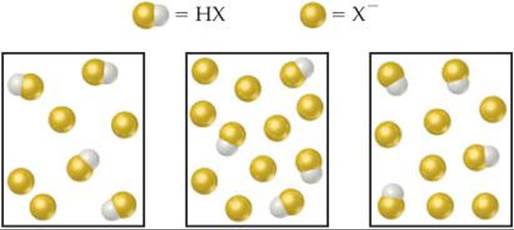
17.1 The following boxes represent aqueous solutions containing a weak acid, HX, and its conjugate base, X–. Water molecules, hydronium ions and cations are not shown. Which solution has the highest pH? Explain. [Section 17.1]
17.2 The beaker on the right contains 0.1 M acetic acid solution with methyl orange as an indicator. The beaker on the left contains a mixture of 0.1 M acetic acid and 0.1 M sodium acetate with methyl orange. (a) Using Figure 16.7, what can you say about the pH of each solution? (b)Which solution is better able to maintain its pH when small amounts of NaOH are added? Explain. [Sections 17.1 and 17.2]

17.3 A buffer contains a weak acid, HX, and its conjugate base. The weak acid has a pKa of 4.5, and the buffer has a pH of 4.3. Without doing a calculation, predict whether [HX] = [X–], [HX] > [X–], or [HX] < [X–]. Explain. [Section 17.2]
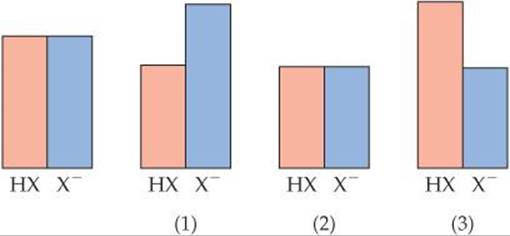
17.4 The drawing on the left represents a buffer composed of equal concentrations of a weak acid, HX, and its conjugate base, X–. The heights of the columns are proportional to the concentrations of the components of the buffer. (a) Which of the three drawings, (1), (2), or (3), represents the buffer after the addition of a strong acid? (b) Which of the three represents the buffer after the addition of a strong base? (c) Which of the three represents a situation that cannot arise from the addition of either an acid or a base? [Section 17.2]
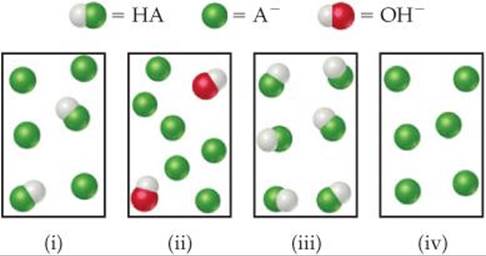
17.5 The following drawings represent solutions at various stages of the titration of a weak acid, HA, with NaOH. (The Na+ ions and water molecules have been omitted for clarity.) To which of the following regions of the titration curve does each drawing correspond: (a) before addition of NaOH, (b) after addition of NaOH but before equivalence point, (c) at equivalence point, (d) after equivalence point? [Section 17.3]
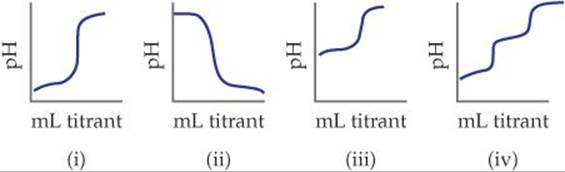
17.6 Match the following descriptions of titration curves with the diagrams: (a) strong acid added to strong base, (b) strong base added to weak acid, (c) strong base added to strong acid, (d) strong base added to polyprotic acid. [Section 17.3]
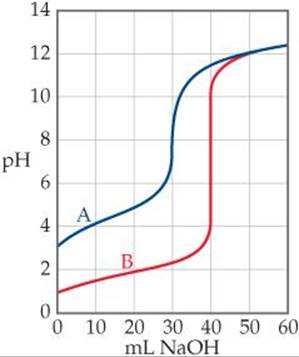
17.7 Equal volumes of two acids are titrated with 0.10 M NaOH resulting in the two titration curves shown in the following figure. (a) Which curve corresponds to the more concentrated acid solution? (b) Which corresponds to the acid with the larger Ka? Explain. [Section 17.3]

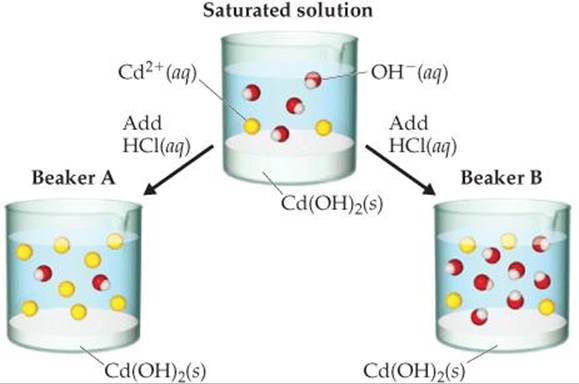
17.8 A saturated solution of Cd(OH)2 is shown in the middle beaker. If hydrochloric acid solution is added, the solubility of Cd(OH)2 will increase, causing additional solid to dissolve. Which of the two choices, Beaker A or Beaker B, accurately represents the solution after equilibrium is reestablished? Explain. (The water molecules and CI– ions are omitted for clarity). [Sections 17.4 and 17.5]
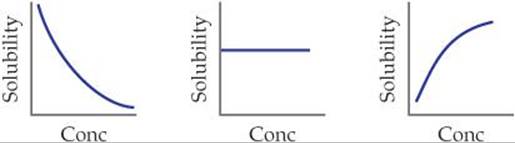
17.9 The following graphs represent the behavior of BaCO3 under different circumstances. In each case the vertical axis indicates the solubility of the BaCO3 and the horizontal axis represents the concentration of some other reagent. (a) Which graph represents what happens to the solubility of BaCO3 as HNO3 is added? (b) Which graph represents what happens to the BaCO3 solubility as Na2CO3 is added? (c) Which represents what happens to the BaCO3 solubility as NaNO3 is added? [Section 17.5]
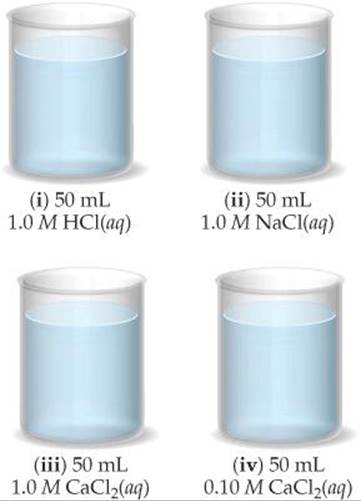
17.10 Ca(OH)2 has a Ksp of 6.5 × 10–6. (a) If 0.370 g of Ca(OH)2 is added to 500 mL of water and the mixture is allowed to come to equilibrium, will the solution be saturated? (b) If 50 mL of the solution from part (a) is added to each of the beakers shown here, in which beakers, if any, will a precipitate form? In those cases where a precipitate forms, what is its identity? [Section 17.6]
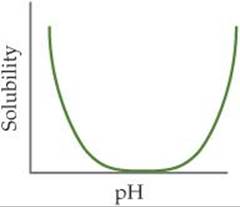
17.11 What is the name given to the kind of behavior demonstrated by a metal hydroxide in this graph? [Section 17.5]
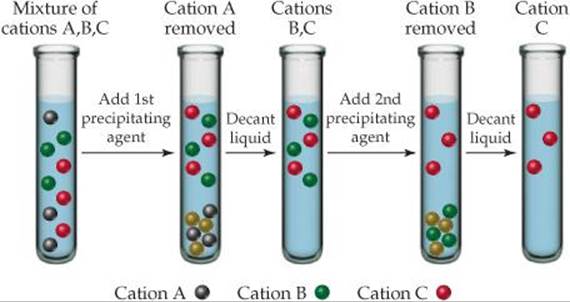
17.12 Three cations, Ni2+, Cu2+, and Ag+, are separated using two different precipitating agents. Based on Figure 17.23, what two precipitating agents could be used? Using these agents, indicate which of the cations is A, which is B, and which is C. [Section 17.7]
COMMON-ION EFFECT (section 17.1)
17.13 (a) What is the common-ion effect? (b) Give an example of a salt that can decrease the ionization of HNO2 in solution.
17.14 (a) Consider the equilibrium B(aq) + H2O(l) ![]() HB+(aq) + OH–(aq). Using Le Châtelier's principle, explain the effect of the presence of a salt of HB+ on the ionization of B. (b) Give an example of a salt that can decrease the ionization of NH3 in solution.
HB+(aq) + OH–(aq). Using Le Châtelier's principle, explain the effect of the presence of a salt of HB+ on the ionization of B. (b) Give an example of a salt that can decrease the ionization of NH3 in solution.
______
17.15 Use information from Appendix D to calculate the pH of (a) a solution that is 0.060 M in potassium propionate (C2H5COOK or KC3H5O2) and 0.085 M in propionic acid (C2H5COOH or HC3H5O2); (b) a solution that is 0.075 M in trimethylamine, (CH3)3N, and 0.10 M in trimethylammonium chloride, (CH3)3NHCl; (c) a solution that is made by mixing 50.0 mL of 0.15 M acetic acid and 50.0 mL of 0.20 M sodium acetate.
17.16 Use information from Appendix D to calculate the pH of (a) a solution that is 0.250 M in sodium formate (HCOONa) and 0.100 M in formic acid (HCOOH); (b) a solution that is 0.510 M in pyridine (C5H5N) and 0.450 M in pyridinium chloride (C5H5NHCl); (c) a solution that is made by combining 55 mL of 0.050 M hydrofluoric acid with 125 mL of 0.10 M sodium fluoride.
______
17.17 (a) Calculate the percent ionization of 0.0075 M butanoic acid (Ka = 1.5 × 10–5). (b) Calculate the percent ionization of 0.0075 M butanoic acid in a solution containing 0.085 M sodium butanoate.
17.18 (a) Calculate the percent ionization of 0.125 M lactic acid (Ka = 1.4 × 10–4). (b) Calculate the percent ionization of 0.125 M lactic acid in a solution containing 0.0075 M sodium lactate.
BUFFERED SOLUTIONS (section 17.2)
17.19 Explain why a mixture of CH3COOH and CH3COONa can act as a buffer while a mixture of HCl and NaCl cannot.
17.20 Explain why a mixture formed by mixing 100 mL of 0.100 M CH3COOH and 50 mL of 0.100 M NaOH will act as a buffer.
______
17.21 (a) Calculate the pH of a buffer that is 0.12 M in lactic acid and 0.11 M in sodium lactate. (b) Calculate the pH of a buffer formed by mixing 85 mL of 0.13 M lactic acid with 95 mL of 0.15 M sodium lactate.
17.22 (a) Calculate the pH of a buffer that is 0.105 M in NaHCO3 and 0.125 M in Na2CO3. (b) Calculate the pH of a solution formed by mixing 65 mL of 0.20 M NaHCO3 with 75 mL of 0.15 M Na2CO3.
______
17.23 A buffer is prepared by adding 20.0 g of sodium acetate (CH3COONa) to 500 mL of a 0.150 M acetic acid (CH3COOH) solution. (a) Determine the pH of the buffer. (b) Write the complete ionic equation for the reaction that occurs when a few drops of hydrochloric acid are added to the buffer. (c) Write the complete ionic equation for the reaction that occurs when a few drops of sodium hydroxide solution are added to the buffer.
17.24 A buffer is prepared by adding 10.0 g of ammonium chloride (NH4Cl) to 250 mL of 1.00 M NH3 solution. (a) What is the pH of this buffer? (b) Write the complete ionic equation for the reaction that occurs when a few drops of nitric acid are added to the buffer. (c) Write the complete ionic equation for the reaction that occurs when a few drops of potassium hydroxide solution are added to the buffer.
______
17.25 You are asked to prepare a pH = 3.00 buffer solution starting from 1.25 L of a 1.00 M solution of hydrofluoric acid (HF) and an excess of sodium fluoride (NaF). (a) What is the pH of the hydrofluoric acid solution prior to adding sodium fluoride? (b) How many grams of sodium fluoride should be added to prepare the buffer solution? Neglect the small volume change that occurs when the sodium fluoride is added.
17.26 You are asked to prepare a pH = 4.00 buffer starting from 1.50 L of 0.0200 M solution of benzoic acid (C6H5COOH) and an excess of sodium benzoate (C6H5COONa). (a) What is the pH of the benzoic acid solution prior to adding sodium benzoate? (b) How many grams of sodium benzoate should be added to prepare the buffer? Neglect the small volume change that occurs when the sodium benzoate is added.
______
17.27 A buffer contains 0.10 mol of acetic acid and 0.13 mol of sodium acetate in 1.00 L. (a) What is the pH of this buffer? (b) What is the pH of the buffer after the addition of 0.02 mol of KOH? (c) What is the pH of the buffer after the addition of 0.02 mol of HNO3?
17.28 A buffer contains 0.15 mol of propionic acid (C2H5COOH) and 0.10 mol of sodium propionate (C2H5COONa) in 1.20 L. (a) What is the pH of this buffer? (b) What is the pH of the buffer after the addition of 0.01 mol of NaOH? (c) What is the pH of the buffer after the addition of 0.01 mol of HI?
______
17.29 (a) What is the ratio of HCO3– to H2CO3 in blood of pH 7.4?
(b) What is the ratio of HCO3– to H2CO3 in an exhausted marathon runner whose blood pH is 7.1?
17.30 A buffer, consisting of H2PO4– and HPO42–, helps control the pH of physiological fluids. Many carbonated soft drinks also use this buffer system. What is the pH of a soft drink in which the major buffer ingredients are 6.5 g of NaH2PO4 and 8.0 g of Na2HPO4 per 355 mL of solution?
______
17.31 You have to prepare a pH 3.50 buffer, and you have the following 0.10 M solutions available: HCOOH, CH3COOH, H3PO4, HCOONa, CH3COONa, and NaH2PO4. Which solutions would you use? How many milliliters of each solution would you use to make approximately a liter of the buffer?
17.32 You have to prepare a pH 5.00 buffer, and you have the following 0.10 M solutions available: HCOOH, HCOONa, CH3COOH, CH3COONa, HCN, and NaCN. Which solutions would you use? How many milliliters of each solution would you use to make approximately a liter of the buffer?
ACID–BASE TITRATIONS (section 17.3)
17.33 The accompanying graph shows the titration curves for two monoprotic acids. (a) Which curve is that of a strong acid? (b) What is the approximate pH at the equivalence point of each titration? (c) 40.0 mL of each acid was titrated with 0.100 M base. Which acid is more concentrated?
17.34 How does titration of a strong, monoprotic acid with a strong base differ from titration of a weak, monoprotic acid with a strong base with respect to the following: (a) quantity of base required to reach the equivalence point, (b) pH at the beginning of the titration, (c) pH at the equivalence point, (d) pH after addition of a slight excess of base, (e) choice of indicator for determining the equivalence point?
______
17.35 The samples of nitric and acetic acid shown here are both titrated with a 0.100 M solution of NaOH(aq).
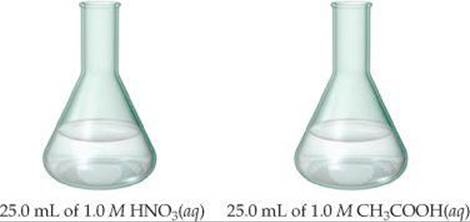
Determine whether each of the following statements concerning these titrations is true or false.
(a) A larger volume of NaOH(aq) is needed to reach the equivalence point in the titration of HNO3.
(b) The pH at the equivalence point in the HNO3 titration will be lower than the pH at the equivalence point in the CH3COOH titration.
(c) Phenolphthalein would be a suitable indicator for both titrations.
17.36 Determine whether each of the following statements concerning the titrations in Problem 17.35 is true or false.
(a) The pH at the beginning of the two titrations will be the same.
(b) The titration curves will both be essentially the same after passing the equivalence point.
(c) Methyl red would be a suitable indicator for both titrations.
______
17.37 Predict whether the equivalence point of each of the following titrations is below, above, or at pH 7: (a) NaHCO3 titrated with NaOH, (b) NH3 titrated with HCl, (c) KOH titrated with HBr.
17.38 Predict whether the equivalence point of each of the following titrations is below, above, or at pH 7: (a) formic acid titrated with NaOH, (b) calcium hydroxide titrated with perchloric acid, (c) pyridine titrated with nitric acid.
______
17.39 As shown in Figure 16.7, the indicator thymol blue has two color changes. Which color change will generally be more suitable for titration of a weak acid with a strong base?
17.40 Assume that 30.0 mL of a 0.10 M solution of a weak base B that accepts one proton is titrated with a 0.10 M solution of the monoprotic strong acid HX. (a) How many moles of HX have been added at the equivalence point? (b) What is the predominant form of B at the equivalence point? (c) What factor determines the pH at the equivalence point? (d) Which indicator, phenolphthalein or methyl red, is likely to be the better choice for this titration?
______
17.41 How many milliliters of 0.0850 M NaOH are required to titrate each of the following solutions to the equivalence point: (a) 40.0 mL of 0.0900 M HNO3, (b) 35.0 mL of 0.0850 M CH3COOH, (c) 50.0 mL of a solution that contains 1.85 g of HCl per liter?
17.42 How many milliliters of 0.105 M HCl are needed to titrate each of the following solutions to the equivalence point: (a) 45.0 mL of 0.0950 M NaOH, (b) 22.5 mL of 0.118 M NH3, (c) 125.0 mL of a solution that contains 1.35 g of NaOH per liter?
______
17.43 A 20.0-mL sample of 0.200 M HBr solution is titrated with 0.200 M NaOH solution. Calculate the pH of the solution after the following volumes of base have been added: (a) 15.0 mL. (b) 19.9 mL, (c) 20.0 mL, (d) 20.1 mL, (e) 35.0 mL.
17.44 A 20.0-mL sample of 0.150 M KOH is titrated with 0.125 M HClO4 solution. Calculate the pH after the following volumes of acid have been added: (a) 20.0 mL, (b) 23.0 mL, (c) 24.0 mL, (d) 25.0 mL, (e) 30.0 mL.
______
17.45 A 35.0-mL sample of 0.150 M acetic acid (CH3COOH) is titrated with 0.150 M NaOH solution. Calculate the pH after the following volumes of base have been added: (a) 0 mL, (b) 17.5 mL, (c) 34.5 mL, (d) 35.0 mL, (e) 35.5 mL, (f) 50.0 mL.
17.46 Consider the titration of 30.0 mL of 0.050 M NH3 with 0.025 M HCl. Calculate the pH after the following volumes of titrant have been added: (a) 0 mL, (b) 20.0 mL, (c) 59.0 mL, (d) 60.0 mL, (e) 61.0 mL, (f) 65.0 mL.
______
17.47 Calculate the pH at the equivalence point for titrating 0.200 M solutions of each of the following bases with 0.200 M HBr: (a) sodium hydroxide (NaOH), (b) hydroxylamine (NH2OH), (c) aniline (C6H5NH2).
17.48 Calculate the pH at the equivalence point in titrating 0.100 M solutions of each of the following with 0.080 M NaOH: (a) hydrobromic acid (HBr), (b) chlorous acid (HClO2), (c) benzoic acid (C6H5COOH).
SOLUBILITY EQUILIBRIA AND FACTORS AFFECTING SOLUBILITY (sections 17.4 and 17.5)
17.49 (a) Why is the concentration of undissolved solid not explicitly included in the expression for the solubility-product constant? (b) Write the expression for the solubility-product constant for each of the following strong electrolytes: AgI, SrSO4, Fe(OH)2, and Hg2Br2.
17.50 (a) Explain the difference between solubility and solubility-product constant. (b) Write the expression for the solubility-product constant for each of the following ionic compounds: MnCO3, Hg(OH)2, and Cu3(PO4)2.
______
17.51 (a) If the molar solubility of CaF2 at 35 °C is 1.24 × 10–3 mol/L, what is Ksp at this temperature? (b) It is found that 1.1 × 10–2 of SrF2 dissolves per 100 mL of aqueous solution at 25 °C. Calculate the solubility product for SrF2. (c) The Ksp of Ba(IO3)2 at 25 °C is 6.0 × 10–10. What is the molar solubility of Ba(IO3)2?
17.52 (a) The molar solubility of PbBr2 at 25 °C is 1.0 × 10–2 mol/L. Calculate Ksp. (b) If 0.0490 g of AgIO3 dissolves per liter of solution, calculate the solubility-product constant. (c) Using the appropriate Ksp value from Appendix D, calculate the pH of a saturated solution of Ca(OH)2.
______
17.53 A 1.00-L solution saturated at 25 °C with calcium oxalate (CaC2O4) contains 0.0061 g of CaC2O4. Calculate the solubility-product constant for this salt at 25 °C.
17.54 A 1.00-L solution saturated at 25 °C with lead(II) iodide contains 0.54 g of PbI2. Calculate the solubility-product constant for this salt at 25 °C.
______
17.55 Using Appendix D, calculate the molar solubility of AgBr in (a) pure water, (b) 3.0 × 10–2M AgNO3 solution, (c) 0.10 M NaBr solution.
17.56 Calculate the solubility of LaF3 in grams per liter in (a) pure water, (b) 0.010 M KF solution, (c) 0.050 M LaCl3 solution.
______
17.57 Consider a beaker containing a saturated solution of CaF2 in equilibrium with undissolved CaF2(s). (a) If solid CaCl2 is added to this solution, will the amount of solid CaF2 at the bottom of the beaker increase, decrease, or remain the same? (b) Will the concentration of Ca2+ ions in solution increase or decrease? (c) Will the concentration of F– ions in solution increase or decrease?
17.58 Consider a beaker containing a saturated solution of Pbl2 in equilibrium with undissolved Pbl2(s). (a) If solid KI is added to this solution, will the amount of solid PbI2 at the bottom of the beaker increase, decrease, or remain the same? (b) Will the concentration of Pb2+ ions in solution increase or decrease? (c) Will the concentration of I– ions in solution increase or decrease?
______
17.59 Calculate the solubility of Mn(OH)2 in grams per liter when buffered at pH (a) 7.0, (b) 9.5, (c) 11.8.
17.60 Calculate the molar solubility of Ni(OH)2 when buffered at pH (a) 8.0, (b) 10.0, (c) 12.0.
______
17.61 Which of the following salts will be substantially more soluble in acidic solution than in pure water: (a) ZnCO3, (b) ZnS, (c) BiI3, (d) AgCN, (e) Ba3(PO4)2?
17.62 For each of the following slightly soluble salts, write the net ionic equation, if any, for reaction with acid: (a) MnS, (b) PbF2, (c) AuCl3, (d) Hg2C2O4, (e) CuBr.
______
17.63 From the value of Kf listed in Table 17.1, calculate the concentration of Ni2+ in 1.0 L of a solution that contains a total of 1 × 10–3 mol of nickel(II) ion and that is 0.20 M in NH3.
17.64 To what final concentration of NH3 must a solution be adjusted to just dissolve 0.020 mol of NiC2O4 (Ksp = 4 × 10–10) in 1.0 L of solution? (Hint: You can neglect the hydrolysis of C2O42– because the solution will be quite basic.)
______
17.65 Use values of Ksp for AgI and Kf for Ag(CN)2– to (a) calculate the molar solubility of AgI in pure water, (b) calculate the equilibrium constant for the reaction
![]()
(c) Determine the molar solubility of AgI in a 0.100 M NaCN solution.
17.66 Using the value of Ksp for Ag2S, Ka1 and Ka2 for H2S, and Kf = 1.1 × 105 for AgCl2–, calculate the equilibrium constant for the following reaction:
![]()
PRECIPITATION AND SEPARATION OF IONS (section 17.6)
17.67 (a) Will Ca(OH)2 precipitate from solution if the pH of a 0.050 M solution of CaCl2 is adjusted to 8.0? (b) Will Ag2SO4 precipitate when 100 mL of 0.050 M AgNO3 is mixed with 10 mL of 5.0 × 10–2M Na2SO4 solution?
17.68 (a) Will Co(OH)2 precipitate from solution if the pH of a 0.020 M solution of Co(NO3)2 is adjusted to 8.5? (b) Will AgIO3 precipitate when 20 mL of 0.010 M AgNO3 is mixed with 10 mL of 0.015 M NaIO3? (Ksp of AgIO3 is 3.1 × 10–8.)
______
17.69 Calculate the minimum pH needed to precipitate Mn(OH)2 so completely that the concentration of Mn2+ is less than 1 μg per liter [1 part per billion (ppb)].
17.70 Suppose that a 10-mL sample of a solution is to be tested for I– ion by addition of 1 drop (0.2 mL) of 0.10 M Pb(NO3)2. What is the minimum number of grams of 1– that must be present for Pbl2(s) to form?
______
17.71 A solution contains 2.0 × 10–4M Ag+ and 1.5 × 10–3M Pb2+. If NaI is added, will AgI (Ksp = 8.3 × 10–17) or PbI2 (Ksp = 7.9 × 10–9) precipitate first? Specify the concentration of l– needed to begin precipitation.
17.72 A solution of Na2SO4 is added dropwise to a solution that is 0.010 M in Ba2+ and 0.010 M in Sr2+. (a) What concentration of SO42– is necessary to begin precipitation? (Neglect volume changes. BaSO4: Ksp = 1.1 × 10–10; SrSO4: Ksp = 3.2 × 10–7.) (b) Which cation precipitates first? (c) What is the concentration of SO42– when the second cation begins to precipitate?
______
17.73 A solution contains three anions with the following concentrations: 0.20 M CrO42–, 0.10 M CO32–, and 0.010 M Cl–. If a dilute AgNO3 solution is slowly added to the solution, what is the first compound to precipitate: Ag2CrO4 (Ksp = 1.2 × 10–12), Ag2CO3 (Ksp = 8.1 × 10–12), or AgCl (Ksp = 1.8 × 10–10)?
17.74 A 1.0 M Na2SO4 solution is slowly added to 10.0 mL of a solution that is 0.20 M in Ca2+ and 0.30 M in Ag+. (a) Which compound will precipitate first: CaSO4 (Ksp = 2.4 × 10–5) or Ag2SO4 (Ksp = 1.5 × 10–5)? (b) How much Na2SO4 solution must be added to initiate the precipitation?
QUALITATIVE ANALYSIS FOR METALLIC ELEMENTS (section 17.7)
17.75 A solution containing an unknown number of metal ions is treated with dilute HCl; no precipitate forms. The pH is adjusted to about 1, and H2S is bubbled through. Again, no precipitate forms. The pH of the solution is then adjusted to about 8. Again, H2S is bubbled through. This time a precipitate forms. The filtrate from this solution is treated with (NH4)2HPO4. No precipitate forms. Which metal ions discussed in Section 17.7 are possibly present? Which are definitely absent within the limits of these tests?
17.76 An unknown solid is entirely soluble in water. On addition of dilute HCl, a precipitate forms. After the precipitate is filtered off, the pH is adjusted to about 1 and H2S is bubbled in; a precipitate again forms. After filtering off this precipitate, the pH is adjusted to 8 and H2S is again added; no precipitate forms. No precipitate forms upon addition of (NH4)2HPO4. The remaining solution shows a yellow color in a flame test (see Figure 7.21). Based on these observations, which of the following compounds might be present, which are definitely present, and which are definitely absent: CdS, Pb(NO3)2, HgO, ZnSO4, Cd(NO3)2, and Na2SO4?
______
17.77 In the course of various qualitative analysis procedures, the following mixtures are encountered: (a) Zn2+ and Cd2+, (b) Cr(OH)3 and Fe(OH)3, (c) Mg2+ and K+, (d) Ag+ and Mn2+. Suggest how each mixture might be separated.
17.78 Suggest how the cations in each of the following solution mixtures can be separated: (a) Na+ and Cd2+, (b) Cu2+ and Mg2+, (c) Pb2+ and Al3+, (d) Ag+ and Hg2+.
______
17.79 (a) Precipitation of the group 4 cations of Figure 17.23 requires a basic medium. Why is this so? (b) What is the most significant difference between the sulfides precipitated in group 2 and those precipitated in group 3? (c) Suggest a procedure that would serve to redissolve the group 3 cations following their precipitation.
17.80 A student who is in a great hurry to finish his laboratory work decides that his qualitative analysis unknown contains a metal ion from group 4 of Figure 17.23. He therefore tests his sample directly with (NH4)2HPO4, skipping earlier tests for the metal ions in groups 1, 2, and 3. He observes a precipitate and concludes that a metal ion from group 4 is indeed present. Why is this possibly an erroneous conclusion?
ADDITIONAL EXERCISES
17.81 Derive an equation similar to the Henderson–Hasselbalch equation relating the pOH of a buffer to the pKb of its base component.
17.82 Benzenesulfonic acid is a monoprotic acid with pKa = 2.25. Calculate the pH of a buffer composed of 0.150 M benzenesulfonic acid and 0.125 M sodium benzenesulfonate.
17.83 Furoic acid (HC5H3O3) has a Ka value of 6.76 × 10–4 at 25 °C. Calculate the pH at 25 °C of (a) a solution formed by adding 25.0 g of furoic acid and 30.0 g of sodium furoate (NaC5H3O3) to enough water to form 0.250 L of solution; (b) a solution formed by mixing 30.0 mL of 0.250 M HC5H3O3 and 20.0 mL of 0.22 M NaC5H3O3 and diluting the total volume to 125 mL; (c) a solution prepared by adding 50.0 mL of 1.65 M NaOH solution to 0.500 L of 0.0850 M HC5H3O3.
17.84 The acid–base indicator bromcresol green is a weak acid. The yellow acid and blue base forms of the indicator are present in equal concentrations in a solution when the pH is 4.68. What is the pKa for bromcresol green?
17.85 Equal quantities of 0.010 M solutions of an acid HA and a base B are mixed. The pH of the resulting solution is 9.2. (a) Write the equilibrium equation and equilibrium-constant expression for the reaction between HA and B. (b) If Ka for HA is 8.0 × 10–5, what is the value of the equilibrium constant for the reaction between HA and B? (c) What is the value of Kb for B?
17.86 Two buffers are prepared by adding an equal number of moles of formic acid (HCOOH) and sodium formate (HCOONa) to enough water to make 1.00 L of solution. Buffer A is prepared using 1.00 mol each of formic acid and sodium formate. Buffer B is prepared by using 0.010 mol of each. (a) Calculate the pH of each buffer, and explain why they are equal. (b) Which buffer will have the greater buffer capacity? Explain. (c) Calculate the change in pH for each buffer upon the addition of 1.0 mL of 1.00 M HCl. (d) Calculate the change in pH for each buffer upon the addition of 10 mL of 1.00 M HCl. (e) Discuss your answers for parts (c) and (d) in light of your response to part (b).
17.87 A biochemist needs 750 mL of an acetic acid–sodium acetate buffer with pH 4.50. Solid sodium acetate (CH3COONa) and glacial acetic acid (CH3COOH) are available. Glacial acetic acid is 99% CH3COOH by mass and has a density of 1.05 g/mL. If the buffer is to be 0.15 M in CH3COOH, how many grams of CH3COONa and how many milliliters of glacial acetic acid must be used?
17.88 A sample of 0.2140 g of an unknown monoprotic acid was dissolved in 25.0 mL of water and titrated with 0.0950 M NaOH. The acid required 27.4 mL of base to reach the equivalence point. (a) What is the molar mass of the acid? (b) After 15.0 mL of base had been added in the titration, the pH was found to be 6.50. What is the Ka for the unknown acid?
17.89 A sample of 0.1687 g of an unknown monoprotic acid was dissolved in 25.0 mL of water and titrated with 0.1150 M NaOH. The acid required 15.5 mL of base to reach the equivalence point. (a) What is the molecular weight of the acid? (b) After 7.25 mL of base had been added in the titration, the pH was found to be 2.85. What is the Ka for the unknown acid?
17.90 Show that the pH at the halfway point of a titration of a weak acid with a strong base (where the volume of added base is half of that needed to reach the equivalence point) is equal to pKa for the acid.
17.91 A hypothetical weak acid, HA, was combined with NaOH in the following proportions: 0.20 mol of HA, 0.080 mol of NaOH. The mixture was diluted to a total volume of 1.0 L and the pH measured. (a) If pH = 4.80, what is the pKa of the acid? (b) How many additional moles of NaOH should be added to the solution to increase the pH to 5.00?
[17.92] What is the pH of a solution made by mixing 0.30 mol NaOH, 0.25 mol Na2HPO4, and 0.20 mol H3PO4 with water and diluting to 1.00 L?
[17.93] Suppose you want to do a physiological experiment that calls for a pH 6.50 buffer. You find that the organism with which you are working is not sensitive to the weak acid H2X (Ka1 = 2 × 10–2; Ka2 = 5.0 × 10–7) or its sodium salts. You have available a 1.0 M solution of this acid and a 1.0 M solution of NaOH. How much of the NaOH solution should be added to 1.0 L of the acid to give a buffer at pH 6.50? (Ignore any volume change.)
[17.94] How many microliters of 1.000 M NaOH solution must be added to 25.00 mL of a 0.1000 M solution of lactic acid [CH3CH(OH)COOH or HC3H5O3] to produce a buffer with pH = 3.75?
17.95 A person suffering from anxiety begins breathing rapidly and as a result suffers alkalosis, an increase in blood pH. (a) Using Equation 17.10, explain how rapid breathing can cause the pH of blood to increase. (b) One cure for this problem is breathing in a paper bag. Why does this procedure lower blood pH?
17.96 For each pair of compounds, use Ksp values to determine which has the greater molar solubility: (a) CdS or CuS, (b) PbCO3 or BaCrO4, (c) Ni(OH)2 or NiCO3, (d) AgI or Ag2SO4.
17.97 The solubility of CaCO3 is pH dependent. (a) Calculate the molar solubility of CaCO3 (Ksp = 4.5 × 10–9) neglecting the acid–base character of the carbonate ion. (b) Use the kb expression for the CO32– ion to determine the equilibrium constant for the reaction
![]()
(c) If we assume that the only sources of Ca2+, HCO3–, and OH– ions are from the dissolution of CaCO3, what is the molar solubility of CaCO3 using the preceding expression? What is the pH? (d) If the pH is buffered at 8.2 (as is historically typical for the ocean), what is the molar solubility of CaCO3? (e) If the pH is buffered at 7.5, what is the molar solubility of CaCO3? How much does this drop in pH increase solubility?
17.98 Tooth enamel is composed of hydroxyapatite, whose sim plest formula is Ca5(PO4)3OH, and whose corresponding Ksp = 6.8 × 10–27. As discussed in the “Chemistry and Life” box on page 730, fluoride in fluorinated water or in tooth paste reacts with hydroxyapatite to form fluoroapatite, Ca5(PO4)3F, whose Ksp = 1.0 × 10–60. (a) Write the expression for the solubility-constant for hydroxyapatite and for fluoroapatite. (b) Calculate the molar solubility of each of these compounds.
17.99 Use the solubility-product constant for Cr(OH)3 (Ksp = 6.7 × 10–31) and the formation constant for Cr(OH)4– from Table 17.1 to determine the concentration of Cr(OH)4– in a solution that is buffered at pH = 10.0 and is in equilibrium with solid Cr(OH)3.
17.100 Calculate the solubility of Mg(OH)2 in 0.50 M NH4Cl.
17.101 The solubility-product constant for barium permanganate, Ba(MnO4)2, is 2.5 × 10–10. Assume that solid Ba(MnO4)2 is in equilibrium with a solution of KMnO4. What concentration of KMnO4 is required to establish a concentration of 2.0 × 10–8M for the Ba2+ ion in solution?
17.102 Calculate the ratio of [Ca2+] to [Fe2+] in a lake in which the water is in equilibrium with deposits of both CaCO3 and FeCO3. Assume that the water is slightly basic and that the hydrolysis of the carbonate ion can therefore be ignored.
[17.103] The solubility products of PbSO4 and SrSO4 are 6.3 × 10–7 and 3.2 × 10–7, respectively. What are the values of [SO42–], [Pb2+], and [Sr2+] in a solution at equilibrium with both substances?
[17.104] A buffer of what pH is needed to give a Mg2+ concentration of 3.0 × 10–2M in equilibrium with solid magnesium oxalate?
[17.105] The value of Ksp for Mg3(AsO4)2 is 2.1 × 10–20. The AsO43– ion is derived from the weak acid H3AsO4 (pKa1 = 2.22; pKa2 = 6.98; pKa3 = 11.50). When asked to calculate the molar solubility of Mg3(AsO4)2 in water, a student used the Ksp expression and assumed that [Mg2+] = 1.5 [AsO43–]. Why was this a mistake?
[17.106] The solubility product for Zn(OH)2 is 3.0 × 10–16. The formation constant for the hydroxo complex, Zn(OH)42–, is 4.6 × 1017. What concentration of OH– is required to dissolve 0.015 mol of Zn(OH)2 in a liter of solution?
[17.107] The value of Ksp for Cd(OH)2 is 2.5 × 10–14. (a) What is the molar solubility of Cd(OH)2? (b) The solubility of Cd(OH)2 can be increased through formation of the complex ion CdBr42– (Kf = 5 × 103). If solid Cd(OH)2 is added to a NaBr solution, what would the initial concentration of NaBr need to be in order to increase the molar solubility of Cd(OH)2 to 1.0 × 10–3 moles per liter?
INTEGRATIVE EXERCISES
17.108 (a) Write the net ionic equation for the reaction that occurs when a solution of hydrochloric acid (HCl) is mixed with a solution of sodium formate (NaCHO2). (b) Calculate the equilibrium constant for this reaction. (c) Calculate the equilibrium concentrations of Na+, Cl–, H+, CHO2–, and HCHO2 when 50.0 mL of 0.15 M HCl is mixed with 50.0 mL of 0.15 M NaCHO2.
17.109 (a) A 0.1044-g sample of an unknown monoprotic acid requires 22.10 mL of 0.0500 M NaOH to reach the end point. What is the molecular weight of the unknown? (b) As the acid is titrated, the pH of the solution after the addition of 11.05 mL of the base is 4.89. What is the Kafor the acid? (c) Using Appendix D, suggest the identity of the acid. Do both the molecular weight and Ka value agree with your choice?
17.110 A sample of 7.5 L of NH3 gas at 22 °C and 735 torr is bubbled into a 0.50-L solution of 0.40 M HCl. Assuming that all the NH3 dissolves and that the volume of the solution remains 0.50 L, calculate the pH of the resulting solution.
17.111 Aspirin has the structural formula
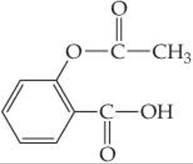
At body temperature (37 °C), Ka for aspirin equals 3 × 10–5. If two aspirin tablets, each having a mass of 325 mg, are dissolved in a full stomach whose volume is 1 L and whose pH is 2, what percent of the aspirin is in the form of neutral molecules?
17.112 What is the pH at 25 °C of water saturated with CO2 at a partial pressure of 1.10 atm? The Henry's law constant for CO2 at 25 °C is 3.1 × 10–2 mol/L-atm. The CO2 is an acidic oxide, reacting with H2O to form H2CO3.
17.113 Excess Ca(OH)2 is shaken with water to produce a saturated solution. The solution is filtered, and a 50.00-mL sample titrated with HCl requires 11.23 mL of 0.0983 M HCl to reach the end point. Calculate Ksp for Ca(OH)2. Compare your result with that in Appendix D. Do you think the solution was kept at 25 °C?
17.114 The osmotic pressure of a saturated solution of strontium sulfate at 25 °C is 21 torr. What is the solubility product of this salt at 25 °C?
17.115 A concentration of 10–100 parts per billion (by mass) of Ag+ is an effective disinfectant in swimming pools. However, if the concentration exceeds this range, the Ag+ can cause adverse health effects. One way to maintain an appropriate concentration of Ag+ is to add a slightly soluble salt to the pool. Using Ksp values from Appendix D, calculate the equilibrium concentration of Ag+ in parts per billion that would exist in equilibrium with (a) AgCl, (b) AgBr, (c) AgI.
[17.116] Fluoridation of drinking water is employed in many places to aid in the prevention of tooth decay. Typically the F– ion concentration is adjusted to about 1 ppb. Some water supplies are also “hard”; that is, they contain certain cations such as Ca2+ that interfere with the action of soap. Consider a case where the concentration of Ca2+ is 8 ppb. Could a precipitate of CaF2 form under these conditions? (Make any necessary approximations.)