CHEMISTRY THE CENTRAL SCIENCE
19 CHEMICAL THERMODYNAMICS
THE SKYLINE OF HONG KONG The construction of our human environment entails the use of enormous amounts of energy to create complex ordered structures, such as modern skyscrapers.
WHAT'S AHEAD
19.1 SPONTANEOUS PROCESSES
We see that changes that occur in nature have a directional character. They move spontaneously in one direction but not in the reverse direction.
19.2 ENTROPY AND THE SECOND LAW OF THERMODYNAMICS
We discuss entropy, a thermodynamic state function that is important in determining whether a process is spontaneous. The second law of thermodynamics tells us that in any spontaneous process the entropy of the universe (system plus surroundings) increases.
19.3 MOLECULAR INTERPRETATION OF ENTROPY
On the molecular level, the entropy of a system is related to the number of accessible microstates. The entropy of the system increases as the randomness of the system increases. The third law of thermodynamics states that, at 0 K, the entropy of a perfect crystalline solid is zero.
19.4 ENTROPY CHANGES IN CHEMICAL REACTIONS
Using tabulated standard molar entropies, we can calculate the standard entropy changes for systems undergoing reaction.
19.5 GIBBS FREE ENERGY
We encounter another thermodynamic state function, free energy (or Gibbs free energy), a measure of how far removed a system is from equilibrium. The change in free energy measures the maximum amount of useful work obtainable from a process and tells us the direction in which a chemical reaction is spontaneous.
19.6 FREE ENERGY AND TEMPERATURE
We consider how the relationship among free-energy change, enthalpy change, and entropy change provides insight into how temperature affects the spontaneity of a process.
19.7 FREE ENERGY AND THE EQUILIBRIUM CONSTANT
Finally, we consider how the standard free-energy change for a chemical reaction can be used to calculate the equilibrium constant for the reaction.
HUMANKIND HAS LEARNED TO HARNESS Earth's resources to create impressive, highly ordered structures, such as the beautiful skyline in the chapter-opening photograph. Our modern society depends heavily on the design of chemical reactions that produce specific useful substances from natural and synthetic materials.
Two of the most important questions chemists ask when designing and using chemical reactions are “How fast is the reaction?” and “How far does it proceed?” The first question is addressed by chemical kinetics, which we discussed in Chapter 14. The second question involves the equilibrium constant, the focus of Chapter 15. Let's briefly review how these concepts are related.
In Chapter 14 we learned that the rate of any chemical reaction is controlled largely by a factor related to energy, namely, the activation energy of the reaction. 
(Section 14.5) In general, the lower the activation energy, the faster a reaction proceeds. In Chapter 15 we saw that chemical equilibrium is reached when a given reaction and its reverse reaction occur at the same rate. (Section 15.1)
Because reaction rates are closely tied to energy, it is logical that equilibrium also depends in some way on energy. In this chapter we explore the connection between energy and the extent of a reaction. Doing so requires a deeper look at chemical thermodynamics, the area of chemistry that deals with energy relationships. We first encountered thermodynamics in Chapter 5, where we discussed the nature of energy, the first law of thermodynamics, and the concept of enthalpy. Recall that the enthalpy change for any system is the heat transferred between the system and its surroundings during a constant-pressure process. (Section 5.3)
In the “Strategies in Chemistry” box in Section 5.4, we pointed out that the enthalpy change that takes place during a reaction is an important guide as to whether the reaction is likely to proceed. Now we will see that reactions involve not only changes in enthalpy but also changes inentropy—another important thermodynamic quantity. Our discussion of entropy will lead us to the second law of thermodynamics, which provides insight into why physical and chemical changes tend to favor one direction over another. We drop a brick, for example, and it falls to the ground. We do not expect the brick to spontaneously rise from the ground to our outstretched hand. We light a candle, and it burns down. We do not expect a half-consumed candle to regenerate itself spontaneously, even if we have captured all the gases produced when the candle burned. Thermodynamics helps us understand the significance of this directional character of processes, regardless of whether they are exothermic or endothermic.
19.1 SPONTANEOUS PROCESSES
The first law of thermodynamics states that energy is conserved. (Section 5.2) In other words, energy is neither created nor destroyed in any process, whether that process is a brick falling, a candle burning, or an ice cube melting. Energy can be transferred between a system and the surroundings and can be converted from one form to another, but the total energy of the universe remains constant. We expressed this law mathematically as ΔE = q + w, where ΔE is the change in the internal energy of a system, q is the heat absorbed (or released) by the system from (or to) the surroundings, and w is the work done on the system by the surroundings, or on the surroundings by the system. Remember that q > 0 means that the system is absorbing heat from the surroundings, and w > 0 means that the surroundings are doing work on the system.
The first law helps us balance the books, so to speak, on the heat transferred between a system and its surroundings and the work done by or on a system. However, because energy is conserved, we can't simply use the value of ΔE to tell us whether a process is favored to occur because anything we do to lower the energy of the system raises the energy of the surroundings, and vice versa. Nevertheless, experience tells us that certain processes always occur, even though the energy of the universe is conserved. Water placed in a freezer turns into ice, for instance, and if you touch a hot object, heat is transferred to your hand. The first law guarantees that energy is conserved in these processes, and yet they occur without any outside intervention. We say they are spontaneous. A spontaneous process is one that proceeds on its own without any outside assistance.
A spontaneous process occurs in one direction only, and the reverse of any spontaneous process is always nonspontaneous. Drop an egg above a hard surface, for example, and it breaks on impact (
FIGURE 19.1). Now, imagine seeing a video clip in which a broken egg rises from the floor, reassembles itself, and ends up in someone's hand. You would conclude that the video is running in reverse because you know that broken eggs simply do not magically rise and reassemble themselves! An egg falling and breaking is spontaneous. The reverse process isnonspontaneous, even though energy is conserved in both processes.
GO FIGURE
Does the potential energy of the eggs change during this process?
FIGURE 19.1 A spontaneous process!
We know other spontaneous and nonspontaneous processes that relate more directly to our study of chemistry. For example, a gas spontaneously expands into a vacuum (
FIGURE 19.2), but the reverse process, in which the gas moves back entirely into one of the flasks, does not happen. In other words, expansion of the gas is spontaneous, but the reverse process is nonspontaneous. In general, processes that are spontaneous in one direction are nonspontaneous in the opposite direction.
Experimental conditions, such as temperature and pressure, are often important in determining whether a process is spontaneous. We are all familiar with situations in which a forward process is spontaneous at one temperature but the reverse process is spontaneous at a different temperature. Consider, for example, ice melting. At atmospheric pressure, when the temperature of the surroundings is above 0 °C, ice melts spontaneously, and the reverse process—liquid water turning into ice—is not spontaneous. However, when the temperature of the surroundings is below 0 °C, the opposite is true—liquid water turns to ice spontaneously, but the reverse process is not spontaneous (
FIGURE 19.3).
GO FIGURE
If flask B were smaller than flask A, would the final pressure after the stopcock is opened be greater than, equal to, or less than 0.5 atm?
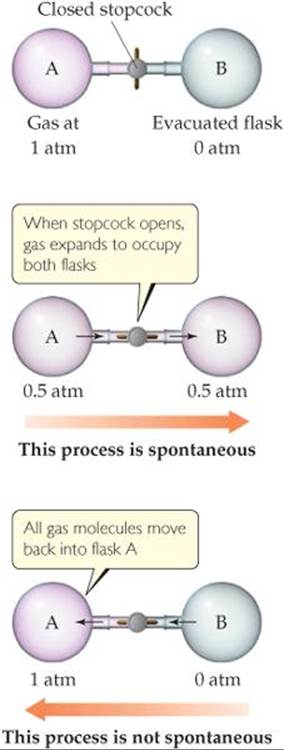
FIGURE 19.2 Expansion of a gas into an evacuated space is a spontaneous process. The reverse process—gas molecules initially distributed evenly in two flasks all moving into one flask—is not spontaneous.
What happens at T = 0 °C, the normal melting point of water, when the flask of Figure 19.3 contains both water and ice? At the normal melting point of a substance, the solid and liquid phases are in equilibrium. (Section 11.6) At this temperature, the two phases are interconverting at the same rate and there is no preferred direction for the process.
It is important to realize that the fact that a process is spontaneous does not necessarily mean that it will occur at an observable rate. A chemical reaction is spontaneous if it occurs on its own accord, regardless of its speed. A spontaneous reaction can be very fast, as in the case of acid–base neutralization, or very slow, as in the rusting of iron. Thermodynamics tells us the direction and extent of a reaction but nothing about the speed.
GIVE IT SOME THOUGHT
If a process is nonspontaneous, does that mean the process cannot occur under any circumstances?
GO FIGURE
In which direction is this process exothermic?
FIGURE 19.3 Spontaneity can depend on temperature. At T > 0 °C, ice melts spontaneously to liquid water. At T < 0 °C, the reverse process, water freezing to ice, is spontaneous. At T = 0 °C the two states are in equilibrium.
SAMPLE EXERCISE 19.1 Identifying Spontaneous Processes
Predict whether each process is spontaneous as described, spontaneous in the reverse direction, or in equilibrium: (a) Water at 40 °C gets hotter when a piece of metal heated to 150 °C is added. (b) Water at room temperature decomposes into H2(g) and O2(g). (c) Benzene vapor, C6H6(g), at a pressure of 1 atm condenses to liquid benzene at the normal boiling point of benzene, 80.1 °C.
SOLUTION
Analyze We are asked to judge whether each process is spontaneous in the direction indicated, in the reverse direction, or in neither direction.
Plan We need to think about whether each process is consistent with our experience about the natural direction of events or whether we expect the reverse process to occur.
Solve
(a) This process is spontaneous. Whenever two objects at different temperatures are brought into contact, heat is transferred from the hotter object to the colder one. (Section 5.1) Thus, heat is transferred from the hot metal to the cooler water. The final temperature, after the metal and water achieve the same temperature (thermal equilibrium), will be somewhere between the initial temperatures of the metal and the water. (b) Experience tells us that this process is not spontaneous—we certainly have never seen hydrogen and oxygen gases spontaneously bubbling up out of water! Rather, the reverse process—the reaction of H2 and O2 to form H2O—is spontaneous. (c) The normal boiling point is the temperature at which a vapor at 1 atm is in equilibrium with its liquid. Thus, this is an equilibrium situation. If the temperature were below 80.1 °C, condensation would be spontaneous.
PRACTICE EXERCISE
At 1 atm pressure, CO2(s) sublimes at –78 °C. Is this process spontaneous at –100 °C and 1 atm pressure?
Answer: No, the reverse process is spontaneous at this temperature.
Seeking a Criterion for Spontaneity
A marble rolling down an incline or a brick falling from your hand loses potential energy. The loss of some form of energy is a common feature of spontaneous change in mechanical systems. During the 1870s Marcellin Bertholet (1827–1907), a famous chemist of that era, suggested that the direction of spontaneous changes in chemical systems is determined by the loss of energy. He proposed that all spontaneous chemical and physical changes are exothermic. It takes only a few moments, however, to find exceptions to this generalization. For example, the melting of ice at room temperature is spontaneous and endothermic. Similarly, many spontaneous dissolution processes, such as the dissolving of NH4NO3, are endothermic, as we discovered in Section 13.1. We conclude that although the majority of spontaneous reactions are exothermic, there are spontaneous endothermic ones as well. Clearly, some other factor must be at work in determining the natural direction of processes.
To understand why certain processes are spontaneous, we need to consider more closely the ways in which the state of a system can change. Recall from Section 5.2 that quantities such as temperature, internal energy, and enthalpy are state functions, properties that define a state and do not depend on how we reach that state. The heat transferred between a system and its surroundings, q, and the work done by or on the system, w, are not state functions—their values depend on the specific path taken between states. One key to understanding spontaneity is understanding differences in the paths between states.
Reversible and Irreversible Processes
In 1824 a 28-year-old French engineer named Sadi Carnot (1796–1832) published an analysis of the factors that determine how efficiently a steam engine can convert heat to work. Carnot considered what an ideal engine, one with the highest possible efficiency, would be like. He observed that it is impossible to convert the energy content of a fuel completely to work because a significant amount of heat is always lost to the surroundings. Carnot's analysis gave insight into how to build better, more efficient engines, and it was one of the earliest studies in what has developed into the discipline of thermodynamics.
An ideal engine operates under an ideal set of conditions in which all the processes are reversible. A reversible process is a specific way in which a system changes its state. In a reversible process, the change occurs in such a way that the system and surroundings can be restored to their original states by exactly reversing the change. In other words, we can restore the system to its original condition with no net change to either the system or its surroundings. An irreversible process is one that cannot simply be reversed to restore the system and its surroundings to their original states. What Carnot discovered is that the amount of work we can extract from any process depends on the manner in which the process is carried out. He concluded that a reversible change produces the maximum amount of work that can be done by a system on its surroundings.
GO FIGURE
If the flow of heat into or out of the system is to be reversible, what must be true of δT?
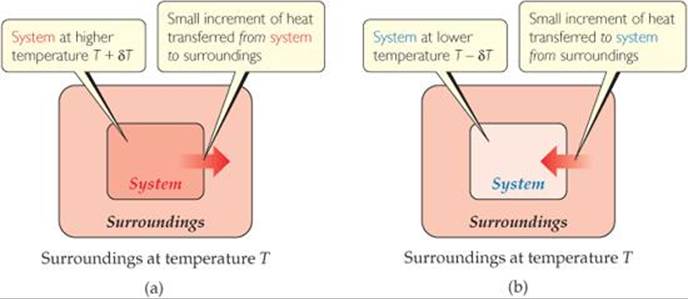
FIGURE 19.4 Reversible flow of heat. Heat can flow reversibly between a system and its surroundings only if the two have an infinitesimally small difference in temperature δT. (a) Increasing the temperature of the system by δT causes heat to flow from the hotter system to the colder surroundings. (b) Decreasing the temperature of the system by δT causes heat to flow from the hotter surroundings to the colder system.
GIVE IT SOME THOUGHT
Suppose you have a system made up of water only, with the container and everything beyond being the surroundings. Consider a process in which the water is first evaporated and then condensed back into its original container. Is this two-step process necessarily reversible?
Let's next examine some aspects of reversible and irreversible processes, first with respect to the transfer of heat. When two objects at different temperatures are in contact, heat flows spontaneously from the hotter object to the colder one. Because it is impossible to make heat flow in the opposite direction, from colder object to hotter one, the flow of heat is an irreversible process. Given these facts, can we imagine any conditions under which heat transfer can be made reversible?
To answer this question, we must consider temperature differences that are infinitesimally small, as opposed to the discrete temperature differences with which we are most familiar. For example, consider a system and its surroundings at essentially the same temperature, with just an infinitesimal temperature difference δT between them (FIGURE 19.4). If the surroundings are at temperature T and the system is at the infinitesimally higher temperature T + δT, then an infinitesimal amount of heat flows from system to surroundings. We can reverse the direction of heat flow by making an infinitesimal change of temperature in the opposite direction, lowering the system temperature to T – δT. Now the direction of heat flow is from surroundings to system. Reversible processes are those that reverse direction whenever an infinitesimal change is made in some property of the system*
Now let's consider another example, the expansion of an ideal gas at constant temperature (referred to as an isothermal process). In the cylinder-piston arrangement of FIGURE 19.5, when the partition is removed, the gas expands spontaneously to fill the evacuated space. Can we determine whether this particular isothermal expansion is reversible or irreversible? Because the gas expands into a vacuum with no external pressure, it does no P-V work on the surroundings. (Section 5.3) Thus, for the expansion, w = 0. We can use the piston to compress the gas back to its original state, but doing so requires that the surroundings do work on the system, meaning that w > 0 for the compression. In other words, the path that restores the system to its original state requires a different value of w (and, by the first law, a different value of q) than the path by which the system was first changed. The fact that the same path can't be followed to restore the system to its original state indicates that the process is irreversible.
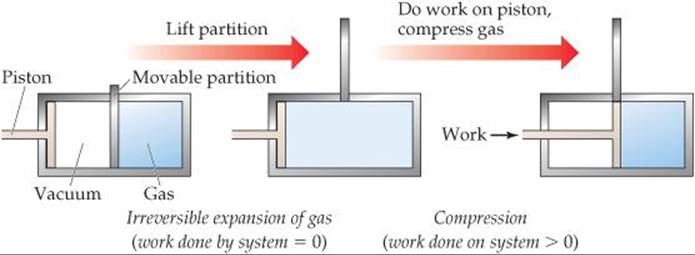
FIGURE 19.5 An irreversible process. Initially an ideal gas is confined to the right half of a cylinder. When the partition is removed, the gas spontaneously expands to fill the whole cylinder. No work is done by the system during this expansion. Using the piston to compress the gas back to its original state requires the surroundings to do work on the system.
What might a reversible isothermal expansion of an ideal gas be? This process will occur only if initially, when the gas is confined to half the cylinder, the external pressure acting on the piston exactly balances the pressure exerted by the gas on the piston. If the external pressure is reduced infinitely slowly, the piston will move outward, allowing the pressure of the confined gas to readjust to maintain the pressure balance. This infinitely slow process in which the external pressure and internal pressure are always in equilibrium is reversible. If we reverse the process and compress the gas in the same infinitely slow manner, we can return the gas to its original volume. The complete cycle of expansion and compression in this hypothetical process, moreover, is accomplished without any net change to the surroundings.
Because real processes can at best only approximate the infinitely slow change associated with reversible processes, all real processes are irreversible. Further, as noted earlier in this discussion, the reverse of any spontaneous process is a nonspontaneous process. A nonspontaneous process can occur only if the surroundings do work on the system. Thus, any spontaneous process is irreversible. Even if we return the system to the original condition, the surroundings will have changed.