CHEMISTRY THE CENTRAL SCIENCE
19 CHEMICAL THERMODYNAMICS
19.3 MOLECULAR INTERPRETATION OF ENTROPY
As chemists, we are interested in molecules. What does entropy have to do with them and with their transformations? What molecular property does entropy reflect? Ludwig Boltzmann (1844–1906) gave conceptual meaning to the notion of entropy, and to understand his contribution, we need to examine the ways in which we can interpret entropy at the molecular level.
Expansion of a Gas at the Molecular Level
In discussing Figure 19.2, we talked about the expansion of a gas into a vacuum as a spontaneous process. We now understand that it is an irreversible process and that the entropy of the universe increases during the expansion. How can we explain the spontaneity of this process at the molecular level? We can get a sense of what makes this expansion spontaneous by envisioning the gas as a collection of particles in constant motion, as we did in discussing the kinetic-molecular theory of gases. 
(Section 10.7) When the stopcock in Figure 19.2 is opened, we can view the expansion of the gas as the ultimate result of the gas molecules moving randomly throughout the larger volume.
Let's look at this idea more closely by tracking two of the gas molecules as they move around. Before the stopcock is opened, both molecules are confined to the left flask, as shown in 
FIGURE 19.6 (a). After the stopcock is opened, the molecules travel randomly throughout the entire apparatus. As Figure 19.6(b) shows, there are four possible arrangements for the two molecules once both flasks are available to them. Because the molecular motion is random, all four arrangements are equally likely. Note that now only one arrangement corresponds to the situation before the stopcock was opened: both molecules in the left flask.
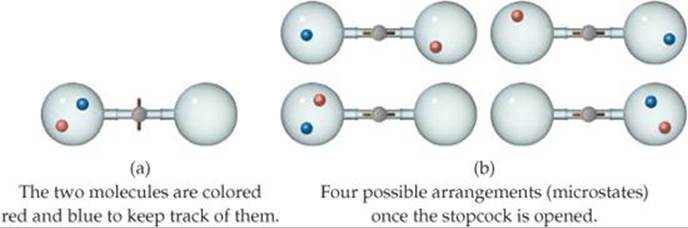
FIGURE 19.6 Possible arrangements of two gas molecules in two flasks. (a) Before the stopcock is opened, both molecules are in the left flask. (b) After the stopcock is opened, there are four possible arrangements of the two molecules.
Figure 19.6(b) shows that with both flasks available to the molecules, the probability of the red molecule being in the left flask is two in four (top right and bottom left arrangements), and the probability of the blue molecule being in the left flask is the same (top left and bottom left arrangements). Because the probability is 2/4 = 1/2 that each molecule is in the left flask, the probability that both are there is 
If we apply the same analysis to three gas molecules, we find that the probability that all three are in the left flask at the same time is 
Now let's consider a mole of gas. The probability that all the molecules are in the left flask at the same time is 
This is a vanishingly small number! Thus, there is essentially zero likelihood that all the gas molecules will be in the left flask at the same time. This analysis of the microscopic behavior of the gas molecules leads to the expected macroscopic 'margin-bottom:0cm;margin-bottom:.0001pt;text-align: justify;text-indent:24.0pt;line-height:normal'>This molecular view of gas expansion shows the tendency of the molecules to “spread out” among the different arrangements they can take. Before the stopcock is opened, there is only one possible arrangement: all molecules in the left flask. When the stopcock is opened, the arrangement in which all the molecules are in the left flask is but one of an extremely large number of possible arrangements. The most probable arrangements by far are those in which there are essentially equal numbers of molecules in the two flasks. When the gas spreads throughout the apparatus, any given molecule can be in either flask rather than confined to the left flask. We say that with the stopcock opened, the arrangement of gas molecules is more random or disordered than when the molecules are all confined in the left flask.
We will see this notion of increasing randomness helps us understand entropy at the molecular level.
Boltzmann's Equation and Microstates
The science of thermodynamics developed as a means of describing the properties of matter in our macroscopic world without regard to microscopic structure. In fact, thermodynamics was a well-developed field before the modern view of atomic and molecular structure was even known. The thermodynamic properties of water, for example, addressed the behavior of bulk water (or ice or water vapor) as a substance without considering any specific properties of individual H2O molecules.
To connect the microscopic and macroscopic descriptions of matter, scientists have developed the field of statistical thermodynamics, which uses the tools of statistics and probability to link the microscopic and macroscopic worlds. Here we show how entropy, which is a property of bulk matter, can be connected to the behavior of atoms and molecules. Because the mathematics of statistical thermodynamics is complex, our discussion will be largely conceptual.
In our discussion of two gas molecules in the two-flask system in Figure 19.6, we saw that the number of possible arrangements helped explain why the gas expands.Suppose we now consider one mole of an ideal gas in a particular ther-modynamic state, which we can define by specifying the temperature, T, and volume, V, of the gas. What is happening to this gas at the microscopic level, and how does what is going on at the microscopic level relate to the entropy of the gas?
FIGURE 19.7 Ludwig Boltzmann's gravestone. Boltzmann's gravestone in Vienna is inscribed with his famous relationship between the entropy of a state, S, and the number of available microstates, W. (In Boltzmann's time, “log” was used to represent the natural logarithm.)
Imagine taking a snapshot of the positions and speeds of all the molecules at a given instant. The speed of each molecule tells us its kinetic energy. That particular set of 6 × 1023 positions and kinetic energies of the individual gas molecules is what we call a microstate of the system. Amicrostate is a single possible arrangement of the positions and kinetic energies of the gas molecules when the gas is in a specific thermodynamic state. We could envision continuing to take snapshots of our system to see other possible microstates.
As you no doubt see, there would be such a staggeringly large number of microstates that taking individual snapshots of all of them is not feasible. Because we are examining such a large number of particles, however, we can use the tools of statistics and probability to determine the total number of microstates for the thermodynamic state. (That is where the statistical part of the name statistical thermodynamics comes in.) Each thermodynamic state hasa characteristic number of microstates associated with it, and we will use the symbol W for that number.
Students sometimes have difficulty distinguishing between the state of a system and the microstates associated with the state. The difference is that state is used to describe the macroscopic view of our system as characterized, for example, by the pressure or temperature of a sample of gas. A microstate is a particular microscopic arrangement of the atoms or molecules of the system that corresponds to the given state of the system. Each of the snapshots we described is a microstate—the positions and kinetic energies of individual gas molecules will change from snapshot to snapshot, but each one is a possible arrangement of the collection of molecules corresponding to a single state. For macroscopically sized systems, such as a mole of gas, there is a very large number of microstates for each state—that is, W is generally an extremely large number.
The connection between the number of microstates of a system, W, and the entropy of the system, S, is expressed in a beautifully simple equation developed by Boltzmann and engraved on his tombstone (FIGURE 19.7):
In this equation, k is Boltzmann's constant, 1.38 × 10–23 J/K. Thus, entropy is a measure of how many microstates are associated with a particular macroscopic state.
GIVE IT SOME THOUGHT
What is the entropy of a system that has only a single microstate?
From Equation 19.5, we see that the entropy change accompanying any process is
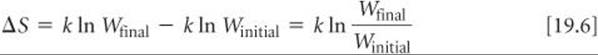
Any change in the system that leads to an increase in the number of microstates (Wfinal > Winitial) leads to a positive value of ΔS: Entropy increases with the number of microstates of the system.
Let's consider two modifications to our ideal-gas sample and see how the entropy changes in each case. First, suppose we increase the volume of the system, which is analogous to allowing the gas to expand isothermally. A greater volume means a greater number of positions available to the gas atoms and therefore a greater number of mi-crostates. The entropy therefore increases as the volume increases, as we saw in the “A Closer Look” box in Section 19.2.
Second, suppose we keep the volume fixed but increase the temperature. How does this change affect the entropy of the system? Recall the distribution of molecular speeds presented in Figure 10.17(a). An increase in temperature increases the most probable speed of the molecules and also broadens the distribution of speeds. Hence, the molecules have a greater number of possible kinetic energies, and the number of microstates increases. Thus, the entropy of the system increases with increasing temperature.
Molecular Motions and Energy
When a substance is heated, the motion of its molecules increases. In Section 10.7, we found that the average kinetic energy of the molecules of an ideal gas is directly proportional to the absolute temperature of the gas. That means the higher the temperature, the faster the molecules move and the more kinetic energy they possess. Moreover, hotter systems have a broader distribution of molecular speeds, as Figure 10.17(a) shows.
The particles of an ideal gas are idealized points with no volume and no bonds, however, points that we visualize as flitting around through space. Any real molecule can undergo three kinds of more complex motion. The entire molecule can move in one direction, which is the simple motion we visualize for an ideal particle and see in a macroscopic object, such as a thrown baseball. We call such movement translational motion. The molecules in a gas have more freedom of translational motion than those in a liquid, which have more freedom of translational motion than the molecules of a solid.
A real molecule can also undergo vibrational motion, in which the atoms in the molecule move periodically toward and away from one another, and rotational motion, in which the molecule spins about an axis. 
FIGURE 19.8 shows the vibrational motions and one of the rotational motions possible for the water molecule. These different forms of motion are ways in which a molecule can store energy, and we refer to the various forms collectively as the motional energy of the molecule.
GIVE IT SOME THOUGHT
What kinds of motion can a molecule undergo that a single atom cannot?
The vibrational and rotational motions possible in real molecules lead to arrangements that a single atom can't have. A collection of real molecules therefore has a greater number of possible microstates than does the same number of ideal-gas particles. In general, the number of microstates possible for a system increases with an increase in volume, an increase in temperature, or an increase in the number of molecules because any of these changes increases the possible positions and kinetic energies of the molecules making up the system. We will also see that the number of microstates increases as the complexity of the molecule increases because there are more vibrational motions available.
Chemists have several ways of describing an increase in the number of microstates possible for a system and therefore an increase in the entropy for the system. Each way seeks to capture a sense of the increased freedom of motion that causes molecules to spread out when not restrained by physical barriers or chemical bonds.
GO FIGURE
Describe another possible rotational motion for this molecule.
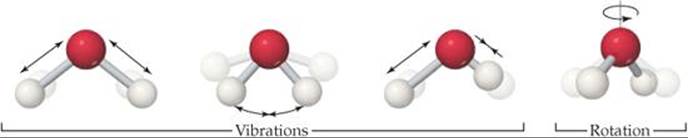
FIGURE 19.8 Vibrational and rotational motions in a water molecule.
The most common way for describing an increase in entropy is as an increase in the randomness, or disorder, of the system. Another way likens an entropy increase to an increased dispersion (spreading out) of energy because there is an increase in the number of ways the positions and energies of the molecules can be distributed throughout the system. Each description (randomness or energy dispersal) is conceptually helpful if applied correctly.
Making Qualitative Predictions About ΔS
It is usually not difficult to estimate qualitatively how the entropy of a system changes during a simple process. As noted earlier, an increase in either the temperature or the volume of a system leads to an increase in the number of microstates, and hence an increase in the entropy. One more factor that correlates with number of microstates is the number of independently moving particles.
We can usually make qualitative predictions about entropy changes by focusing on these factors. For example, when water vaporizes, the molecules spread out into a larger volume. Because they occupy a larger volume, there is an increase in their freedom of motion, giving rise to a greater number of possible microstates, and hence an increase in entropy.
Now consider the phases of water. In ice, hydrogen bonding leads to the rigid structure shown in FIGURE 19.9. Each molecule in the ice is free to vibrate, but its translational and rotational motions are much more restricted than in liquid water. Although there are hydrogen bonds in liquid water, the molecules can more readily move about relative to one another (translation) and tumble around (rotation). During melting, therefore, the number of possible microstates increases and so does the entropy. In water vapor, the molecules are essentially independent of one another and have their full range of translational, vibrational, and rotational motions. Thus, water vapor has an even greater number of possible microstates and therefore a higher entropy than liquid water or ice.
GO FIGURE
In which phase are water molecules least able to have rotational motion?
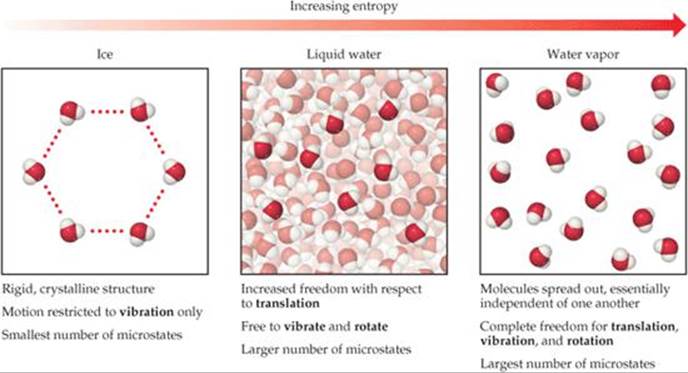
FIGURE 19.9 Entropy and the phases of water. The larger the number of possible microstates, the higher the entropy of the system.
When an ionic solid dissolves in water, a mixture of water and ions replaces the pure solid and pure water, as shown for KCl in 
FIGURE 19.10. The ions in the liquid move in a volume that is larger than the volume in which they were able to move in the crystal lattice and so possess more motional energy. This increased motion might lead us to conclude that the entropy of the system has increased. We have to be careful, however, because some of the water molecules have lost some freedom of motion because they are now held around the ions as water of hydration. (Section 13.1) These water molecules are in a more ordered state than before because they are now confined to the immediate environment of the ions. Therefore, the dissolving of a salt involves both a disordering process (the ions become less confined) and an ordering process (some water molecules become more confined). The disordering processes are usually dominant, and so the overall effect is an increase in the randomness of the system when most salts dissolve in water.
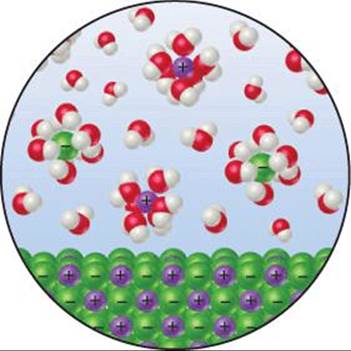
FIGURE 19.10 Entropy changes when an ionic solid dissolves in water. The ions become more spread out and disordered, but the water molecules that hydrate the ions become less disordered.
The same ideas apply to chemical reactions. Consider the reaction between nitric oxide gas and oxygen gas to form nitrogen dioxide gas:
which results in a decrease in the number of molecules—three molecules of gaseous reactants form two molecules of gaseous products (FIGURE 19.11). The formation of new N—O bonds reduces the motions of the atoms in the system. The formation of new bonds decreases the number of degrees of freedom, or forms of motion, available to the atoms. That is, the atoms are less free to move in random fashion because of the formation of new bonds. The decrease in the number of molecules and the resultant decrease in motion result in fewer possible microstates and therefore a decrease in the entropy of the system.
In summary, we generally expect the entropy of a system to increase for processes in which
1. Gases form from either solids or liquids.
2. Liquids or solutions form from solids.
3. The number of gas molecules increases during a chemical reaction.
SAMPLE EXERCISE 19.3 Predicting the Sign of ΔS
Predict whether ΔS is positive or negative for each process, assuming each occurs at constant temperature:
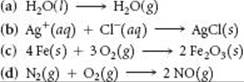
SOLUTION
Analyze We are given four reactions and asked to predict the sign of ΔS for each.
Plan We expect ΔS to be positive if there is an increase in temperature, increase in volume, or increase in number of gas particles. The question states that the temperature is constant, and so we need to concern ourselves only with volume and number of particles.
Solve
(a) Evaporation involves a large increase in volume as liquid changes to gas. One mole of water (18 g) occupies about 18 mL as a liquid and if it could exist as a gas at STP it would occupy 22.4 L. Because the molecules are distributed throughout a much larger volume in the gaseous state, an increase in motional freedom accompanies vaporization and ΔS is positive.
(b) In this process, ions, which are free to move throughout the volume of the solution, form a solid, in which they are confined to a smaller volume and restricted to more highly constrained positions. Thus, ΔS is negative.
(c) The particles of a solid are confined to specific locations and have fewer ways to move (fewer microstates) than do the molecules of a gas. Because O2 gas is converted into part of the solid product Fe2O3, ΔS is negative.
(d) The number of moles of reactant gases is the same as the number of moles of product gases, and so the entropy change is expected to be small. The sign of ΔS is impossible to predict based on our discussions thus far, but we can predict that ΔS will be close to zero.
PRACTICE EXERCISE
Indicate whether each process produces an increase or decrease in the entropy of the system:
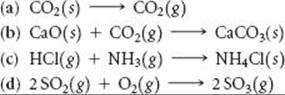
Answers: (a) increase, (b) decrease, (c) decrease, (d) decrease
GO FIGURE
What major factor leads to a decrease in entropy as the reaction shown takes place?
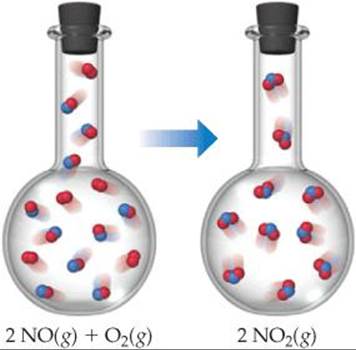
FIGURE 19.11 Entropy decreases when NO(g) is oxidized by O2(g) to NO2(g). A decrease in the number of gaseous molecules leads to a decrease in the entropy of the system.
SAMPLE EXERCISE 19.4 Predicting Relative Entropies
In each pair, choose the system that has greater entropy and explain your choice: (a) 1 mol of NaCl(s) or 1 mol of HCl(g) at 25 °C, (b) 2 mol of HCl(g) or 1 mol of HCl(g) at 25 °C, (c) 1 mol of HCl(g) or 1 mol of Ar(g) at 298 K.
SOLUTION
Analyze We need to select the system in each pair that has the greater entropy.
Plan We examine the state of each system and the complexity of the molecules it contains.
Solve
(a) HCl(g) has the higher entropy because the particles in gases are more disordered and have more freedom of motion than the particles in solids. (b) When these two systems are at the same pressure, the sample containing 2 mol of HCl has twice the number of molecules as the sample containing 1 mol. Thus, the 2-mol sample has twice the number of microstates and twice the entropy. (c) The HCl system has the higher entropy because the number of ways in which an HCl molecule can store energy is greater than the number of ways in which an Ar atom can store energy. (Molecules can rotate and vibrate; atoms cannot.)
PRACTICE EXERCISE
Choose the system with the greater entropy in each case: (a) 1 mol of H2(g) at STP or 1 mol of H2(g) at 100 °C and 0.5 atm, (b) 1 mol of H2O(s) at 0 °C or 1 mol of H2O(l) at 25 °C, (c) 1 mol of H2(g) at STP or 1 mol of SO2(g) at STP, (d) 1 mol of N2O4(g) at STP or 2 mol of NO2(g) at STP.
Answers: (a) 1 mol of H2(g) at 100 °C and 0.5 atm, (b) 1 mol of H2O(l) at 25 °C, (c) 1 mol of SO2(g) at STP, (d) 2 mol of NO2(g) at STP
The Third Law of Thermodynamics
If we decrease the thermal energy of a system by lowering the temperature, the energy stored in translational, vibrational, and rotational motion decreases. As less energy is stored, the entropy of the system decreases. If we keep lowering the temperature, do we reach a state in which these motions are essentially shut down, a point described by a single microstate? This question is addressed by the third law of thermodynamics, which states that the entropy of a pure crystalline substance at absolute zero is zero: S(0 K) = 0.
Consider a pure crystalline solid. At absolute zero, the individual atoms or molecules in the lattice would be perfectly ordered and as well defined in position as they could be. Because none of them would have thermal motion, there is only one possible microstate. As a result, Equation 19.5 becomes S = k ln W = k ln 1 = 0. As the temperature is increased from absolute zero, the atoms or molecules in the crystal gain energy in the form of vibrational motion about their lattice positions. This means that the degrees of freedom and the entropy both increase. What happens to the entropy, however, as we continue to heat the crystal? We consider this important question in the next section.
GIVE IT SOME THOUGHT
If you are told that the entropy of a system is zero, what do you know about the system?
CHEMISTRY AND LIFE
ENTROPY AND HUMAN SOCIETY
The laws of thermodynamics have profound implications for our existence. In the “Chemistry Put to Work” box on page 192, we examined some of the scientific and political challenges of using biofuels as a major energy source to maintain our lifestyles. That discussion builds around the first law of thermodynamics, namely, that energy is conserved. We therefore have important decisions to make as to energy production and consumption.
The second law of thermodynamics is also relevant in discussions about our existence and about our ability and desire to advance as a civilization. Any living organism is a complex, highly organized, well-ordered system. Our entropy content is much lower than it would be if we were completely decomposed into carbon dioxide, water, and several other simple chemicals. Does this mean that our existence is a violation of the second law? No, because the thousands of chemical reactions necessary to produce and maintain human life have caused a very large increase in the entropy of the rest of the universe. Thus, as the second law requires, the overall entropy change during the lifetime of a human, or any other living system, is positive.
In addition to being complex living systems ourselves, we humans are masters of producing order in the world around us. As shown in the chapter-opening photograph, we build impressive, highly ordered structures and buildings. We manipulate and order matter at the nanoscale level in order to produce the technological breakthroughs that have become so commonplace in the twenty-first century (FIGURE 19.12). We use tremendous quantities of raw materials to produce highly ordered materials—iron, copper, and a host of other metals from their ores, silicon for computer chips from sand, polymers from fossil fuel feedstocks, and so forth. In so doing, we expend a great deal of energy to, in essence, “fight” the second law of thermodynamics.
For every bit of order we produce, however, we produce an even greater amount of disorder. Petroleum, coal, and natural gas are burned to provide the energy necessary for us to achieve highly ordered structures, but their combustion increases the entropy of the universe by releasing CO2(g), H2O(g), and heat. Oxide and sulfide ores release CO2(g) and SO2(g) that spread throughout our atmosphere. Thus, even as we strive to create more impressive discoveries and greater order in our society, we drive the entropy of the universe higher, as the second law says we must.
We humans are, in effect, using up our storehouse of energy-rich materials to create order and advance technology. As noted in Chapter 5, we must learn to harness new energy sources, such as solar energy, before we exhaust the supplies of readily available energy of other kinds.
FIGURE 19.12 Fighting the second law. Creating complex structures, such as the skyscrapers in the chapter-opening photograph, requires that we use energy to produce order while knowing that we are increasing the entropy of the universe. Modern cellular telephones, with their detailed displays and complex circuitry are an example on a smaller scale of the impressive order that human ingenuity achieves.