CHEMISTRY THE CENTRAL SCIENCE

19 CHEMICAL THERMODYNAMICS

19.6 FREE ENERGY AND TEMPERATURE

Tabulations of , such as those in Appendix C, make it possible to calculate ΔG° for reactions at the standard temperature of 25 °C, but we are often interested in examining reactions at other temperatures. To see how ΔG is affected by temperature, let's look again at Equation 19.11:

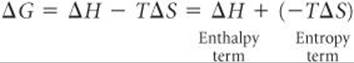
Notice that we have written the expression for ΔG as a sum of two contributions, an enthalpy term, ΔH, and an entropy term, –TΔS. Because the value of –TΔS depends directly on the absolute temperature T, ΔG varies with temperature. We know that the enthalpy term, ΔH, can be either positive or negative and that T is positive at all temperatures other than absolute zero. The entropy term, –TΔS, can also be positive or negative. When ΔS is positive, which means the final state has greater randomness (a greater number of microstates) than the initial state, the term –TΔS is negative. When ΔS is negative, –TΔS is positive.

The sign of ΔG, which tells us whether a process is spontaneous, depends on the signs and magnitudes of ΔH and –TΔS. The various combinations of ΔH and –TΔS signs are given in TABLE 19.3.

Note in Table 19.3 that when ΔH and –TΔS have opposite signs, the sign of ΔG depends on the magnitudes of these two terms. In these instances temperature is an important consideration. Generally, ΔH and ΔS change very little with temperature. However, the value of T directly affects the magnitude of – TΔS. As the temperature increases, the magnitude of –TΔS increases, and this term becomes relatively more important in determining the sign and magnitude of ΔG.

As an example, let's consider once more the melting of ice to liquid water at 1 atm:

This process is endothermic, which means that ΔH is positive. Because the entropy increases during the process, ΔS is positive, which makes –TΔS negative. At temperatures below 0 °C (273 K), the magnitude of ΔH is greater than that of –TΔS. Hence, the positive enthalpy term dominates, and ΔG is positive. This positive value of ΔG means that ice melting is not spontaneous at T < 0 °C, just as our everyday experience tells us; rather, the reverse process, the freezing of liquid water into ice, is spontaneous at these temperatures.

What happens at temperatures greater than 0 °C? As T increases, so does the magnitude of –TΔS. When T > 0 °C, the magnitude of –TΔS is greater than the magnitude of ΔH, which means that the –TΔS term dominates and ΔG is negative. The negative value of ΔG tells us that ice melting is spontaneous at T > 0 °C.

At the normal melting point of water, T = 0 °C, the two phases are in equilibrium. Recall that ΔG = 0 at equilibrium; at T = 0 °C, ΔH and –TΔS are equal in magnitude and opposite in sign, so they cancel and give ΔG = 0.

TABLE 19.3 • How Signs of ΔH and ΔS Affect Reaction Spontaneity

GIVE IT SOME THOUGHT

The normal boiling point of benzene is 80 °C. At 100 °C and 1 atm, which term is greater in magnitude for the vaporization of benzene, ΔH or TΔS?

Our discussion of the temperature dependence of ΔG is also relevant to standard free-energy changes. We can calculate the values of ΔH° and ΔS° at 298 K from the data in Appendix C. If we assume that these values do not change with temperature, we can then use Equation 19.12 to estimate ΔG° at temperatures other than 298 K.

SAMPLE EXERCISE 19.9 Determining the Effect of Temperature on Spontaneity

The Haber process for the production of ammonia involves the equilibrium

Assume that ΔH° and ΔS° for this reaction do not change with temperature. (a) Predict the direction in which ΔG° for the reaction changes with increasing temperature. (b) Calculate ΔG° at 25 °C and 500 °C.

SOLUTION

Analyze In part (a) we are asked to predict the direction in which ΔG° changes as temperature increases. In part (b) we need to determine ΔG° for the reaction at two temperatures.

Plan We can answer part (a) by determining the sign of ΔS for the reaction and then using that information to analyze Equation 19.12. In part (b) we first calculate ΔH° and ΔS° for the reaction using data in Appendix C and then use Equation 19.12 to calculate ΔG°.

Solve

(a) The temperature dependence of ΔG° comes from the entropy term in Equation 19.12, ΔG° = ΔH° –TΔS°. We expect ΔS° for this reaction to be negative because the number of molecules of gas is smaller in the products. Because ΔS° is negative, –TΔS° is positive and increases with increasing temperature. As a result, ΔG° becomes less negative (or more positive) with increasing temperature. Thus, the driving force for the production of NH₃ becomes smaller with increasing temperature.

(b) We calculated ΔH° for this reaction in Sample Exercise 15.14 and ΔS° in Sample Exercise 19.5: ΔH° = –92.38 kJ and ΔS° = –198.3 J/K. If we assume that these values do not change with temperature, we can calculate ΔG° at any temperature by using Equation 19.12. At T = 25 °C = 298 K, we have

At T = 500°C = 773 K, we have

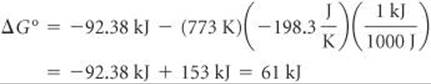
Notice that we had to convert the units of –TΔS° to kJ in both calculations so that this term can be added to the ΔH° term, which has units of kJ.

Comment Increasing the temperature from 298 K to 773 K changes ΔG° from –33.3 kJ to + 61 kJ. Of course, the result at 773 K assumes that ΔH° and ΔS° do not change withtemperature. Although these values do change slightly with temperature, the result at 773 K shouldbe a reasonable approximation.

The positive increase in ΔG° with increasing T agrees with our prediction in part (a). Our result indicates that in a mixture of N₂(g), H₂(g), and NH₃(g), each present at a partial pressure of 1 atm, the N₂(g) and H₂(g) react spontaneously at 298 K to form more NH₃(g). At 773 K, the positive value of ΔG° tells us that the reverse reaction is spontaneous. Thus, when the mixture of these gases, each at a partial pressure of 1 atm, is heated to 773 K, some of the NH₃(g) spontaneously decomposes into N₂(g) and H₂(g).

PRACTICE EXERCISE

(a) Using standard enthalpies of formation and standard entropies in Appendix C, calculate ΔH° and ΔS° at 298 K for the reaction 2 SO₂(g) + O₂(g) → 2 SO₃(g). (b) Use your values from part (a) to estimate ΔG° at 400 K.

Answers: