CHEMISTRY THE CENTRAL SCIENCE
20 ELECTRO-CHEMISTRY
20.2 BALANCING REDOX EQUATIONS
Whenever we balance a chemical equation, we must obey the law of conservation of mass: The amount of each element must be the same on both sides of the equation. (Atoms are neither created nor destroyed in any chemical reaction.) As we balance oxidation-reduction reactions, there is an additional requirement: The gains and losses of electrons must be balanced. If a substance loses a certain number of electrons during a reaction, another substance must gain that same number of electrons. (Electrons are neither created nor destroyed in any chemical reaction.)
In many simple chemical equations, such as Equation 20.2, balancing the electrons is handled “automatically” in the sense that we can balance the equation without explicitly considering the transfer of electrons. Many redox equations are more complex than Equation 20.2, however, and cannot be balanced easily without taking into account the number of electrons lost and gained. In this section we examine the method of half-reactions, a systematic procedure for balancing redox equations.
Half-Reactions
Although oxidation and reduction must take place simultaneously, it is often convenient to consider them as separate processes. For example, the oxidation of Sn2+ by Fe3+,
can be considered as consisting of two processes: oxidation of Sn2+ and reduction of Fe3+:
Notice that electrons are shown as products in the oxidation process and as reactants in the reduction process.
Equations that show either oxidation or reduction alone, such as Equations 20.4 and 20.5, are called half-reactions. In the overall redox reaction, the number of electrons lost in the oxidation half-reaction must equal the number of electrons gained in the reduction half-reaction. When this condition is met and each half-reaction is balanced, the electrons on the two sides cancel when the two half-reactions are added to give the balanced oxidation-reduction equation.
Balancing Equations by the Method of Half-Reactions
In using the half-reaction method, we usually begin with a “skeleton” ionic equation showing only the substances undergoing oxidation and reduction. In such cases, we usually do not need to assign oxidation numbers unless we are unsure whether the reaction involves oxidation-reduction. We will find that H+ (for acidic solutions), OH– (for basic solutions), and H2O are often involved as reactants or products in redox reactions. Unless H+, OH–, or H2O is being oxidized or reduced, these species do not appear in the skeleton equation. Their presence, however, can be deduced as we balance the equation.
For balancing a redox reaction that occurs in acidic aqueous solution, the procedure is as follows:
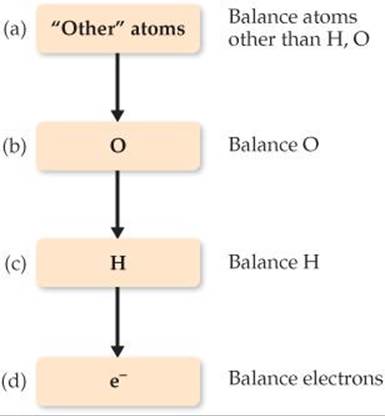
1. Divide the equation into one oxidation half-reaction and one reduction half-reaction.
2. Balance each half-reaction.
(a) First, balance elements other than H and O.
(b) Next, balance O atoms by adding H2O as needed.
(c) Then balance H atoms by adding H+ as needed.
(d) Finally, balance charge by adding e– as needed.
This specific sequence (a)–(d) is important, and it is summarized in the diagram in the margin. At this point, you can check whether the number of electrons in each half-reaction corresponds to the changes in oxidation state.
3. Multiply half-reactions by integers as needed to make the number of electrons lost in the oxidation half-reaction equal the number of electrons gained in the reduction half-reaction.
4. Add half-reactions and, if possible, simplify by canceling species appearing on both sides of the combined equation.
5. Check to make sure that atoms and charges are balanced.
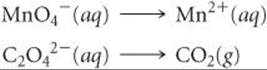
As an example, let's consider the reaction between permanganate ion (MnO4–) and oxalate ion (C2O42–) in acidic aqueous solution (
FIGURE 20.2). When MnO4– is added to an acidified solution of C2O42–, the deep purple color of the MnO4– ion fades, bubbles of CO2 form, and the solution takes on the pale pink color of Mn2+. We can therefore write the skeleton equation as
Experiments show that H+ is consumed and H2O is produced in the reaction. We will see that their involvement in the reaction is deduced in the course of balancing the equation.
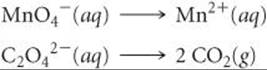
To complete and balance Equation 20.6, we first write the two half-reactions (step 1). One half-reaction must have Mn on both sides of the arrow, and the other must have C on both sides of the arrow:
We next complete and balance each half-reaction. First, we balance all the atoms except H and O (step 2a). In the permanganate half-reaction, we have one manganese atom on each side of the equation and so need to do nothing. In the oxalate half-reaction, we add a coefficient 2 on the right to balance the two carbons on the left:
Next we balance O (step 2b). The permanganate half-reaction has four oxygens on the left and none on the right; therefore we need four H2O molecules on the right to balance the oxygen atoms:
GO FIGURE
Which species is reduced in this reaction? Which species is the reducing agent?
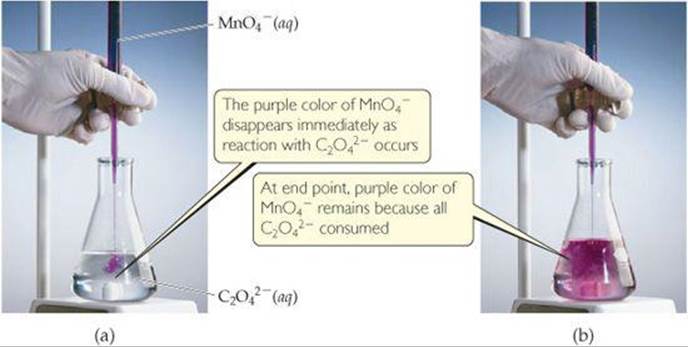
FIGURE 20.2 Titration of an acidic solution of Na2C2O4 with KMnO4(aq).
The eight hydrogen atoms now in the products must be balanced by adding 8 H+ to the reactants (step 2c):
There are now equal numbers of each type of atom on the two sides of the equation, but the charge still needs to be balanced. The charge of the reactants is 8(1+) +1(1–) = 7+, and that of the products is 1(2+) +4(0) = 2+. To balance the charge, we add five electrons to the reactant side (step 2d):
We can use oxidation states to check our result. In this half-reaction Mn goes from the +7 oxidation state in MnO4– to the +2 oxidation state of Mn2+. Therefore, each Mn atom gains five electrons, in agreement with our balanced half-reaction.
In the oxalate half-reaction, we have C and O balanced (step 2a). We balance the charge (step 2d) by adding two electrons to the products:
We can check this result using oxidation states. Carbon goes from the +3 oxidation state in C2O42– to the +4 oxidation state in CO2. Thus, each C atom loses one electron; therefore, the two C atoms in C2O42– lose two electrons, in agreement with our balanced half-reaction.
Now we multiply each half-reaction by an appropriate integer so that the number of electrons gained in one half-reaction equals the number of electrons lost in the other (step 3). We multiply the MnO4– half-reaction by 2 and the C2O42– half-reaction by 5:
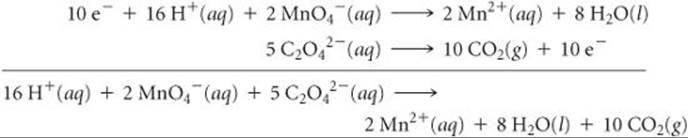
The balanced equation is the sum of the balanced half-reactions (step 4). Note that the electrons on the reactant and product sides of the equation cancel each other.
We check the balanced equation by counting atoms and charges (step 5): There are 16 H, 2 Mn, 28 O, 10 C, and a net charge of 4+ on each side of the equation, confirming that the equation is correctly balanced.
GIVE IT SOME THOUGHT
Do free electrons appear anywhere in the balanced equation for a redox reaction?
SAMPLE EXERCISE 20.2 Balancing Redox Equations in Acidic Solution
Complete and balance this equation by the method of half-reactions:
SOLUTION
Analyze We are given an incomplete, unbalanced (skeleton) equation for a redox reaction occurring in acidic solution and asked to complete and balance it.
Plan We use the half-reaction procedure we just learned.
Solve
Step 1: We divide the equation into two half-reactions:
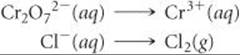
Step 2: We balance each half-reaction. In the first half-reaction the presence of one Cr2O72– among the reactants requires two Cr3+ among the products. The seven oxygen atoms in Cr2O72– are balanced by adding seven H2O to the products. The 14 hydrogen atoms in 7 H2O are then balanced by adding 14 H+ to the reactants:
We then balance the charge by adding electrons to the left side of the equation so that the total charge is the same on the two sides:
We can check this result by looking at the oxidation state changes. Each chromium atom goes from +6 to +3, gaining three electrons; therefore, the two Cr atoms in Cr2O72– gain six electrons, in agreement with our half-reaction.
In the second half-reaction, two Cl– are required to balance one Cl2:
We add two electrons to the right side to attain charge balance:
This result agrees with the oxidation state changes. Each chlorine atom goes from –1 to 0, losing one electron; therefore, the two chlorine atoms lose two electrons.
Step 3: We equalize the number of electrons transferred in the two half-reactions. To do so, we multiply the Cl half-reaction by 3 so that the number of electrons gained in the Cr half-reaction (6) equals the number lost in the Cl half-reaction, allowing the electrons to cancel when the half-reactions are added:
Step 4: The equations are added to give the balanced equation:
Step 5: There are equal numbers of atoms of each kind on the two sides of the equation (14 H, 2 Cr, 7 O, 6 Cl). In addition, the charge is the same on the two sides (6+). Thus, the equation is balanced.
PRACTICE EXERCISE
Complete and balance the following equations using the method of half-reactions. Both reactions occur in acidic solution.
Answers: 
Balancing Equations for Reactions Occurring in Basic Solution
If a redox reaction occurs in basic solution, the equation must be balanced by using OH– and H2O rather than H and H2O. One approach is to first balance the half-reactions as if they occurred in acidic solution and then count the number of H in each half-reaction and add the same number of OH–to each side of the half-reaction. This way, the reaction is mass-balanced because you are adding the same thing to both sides. In essence, what you are doing is “neutralizing” the protons to form water (H+ + OH– → H2O) on the side containing H+, and the other side ends up with the OH–. The resulting water molecules can be canceled as needed.
SAMPLE EXERCISE 20.3 Balancing Redox Equations in Basic Solution
Complete and balance this equation for a redox reaction that takes place in basic solution:
SOLUTION
Analyze We are given an incomplete equation for a basic redox reaction and asked to balance it.
Plan We go through the first steps of our procedure as if the reaction were occurring in acidic solution. We then add the appropriate number of OH– ions to each side of the equation, combining H+ and OH– to form H2O. We complete the process by simplifying the equation.
Solve
Step 1: We write the incomplete, unbalanced half-reactions:
Step 2: We balance each half-reaction as if it took place in acidic solution:
Now we must take into account that the reaction occurs in basic solution, adding OH– to both sides of both half-reactions to neutralize H+:
We “neutralize” H+ and OH– by forming H2O when they are on the same side of either half-reaction:
Next, we cancel water molecules that appear as both reactants and products:
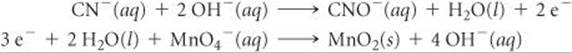
Both half-reactions are now balanced. You can check the atoms and the overall charge.
Step 3: We multiply the cyanide half-reaction by 3, which gives 6 electrons on the product side, and multiply the permanganate half-reaction by 2, which gives 6 electrons on the reactant side:
Step 4: We add the two half-reactions together and simplify by canceling species that appear as both reactants and products:
Step 5: Check that the atoms and charges are balanced.
There are 3 C, 3 N, 2 H, 9 O, 2 Mn, and a charge of 5– on both sides of the equation.
Comment It is important to remember that this procedure doesn't imply that H+ ions are involved in the chemical reaction. Recall that in aqueous solutions at 20°C, Kw = [H+][OH–] = 1.0 × 10–14. Thus, [H+] is very small in this basic solution. 
(Section 16.3)
PRACTICE EXERCISE
Complete and balance the following equations for oxidation-reduction reactions that occur in basic solution:
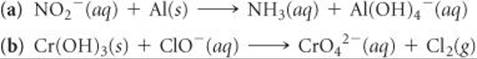
Answer: 
GO FIGURE
Why does the intensity of the blue solution color lessen as the reaction proceeds?
FIGURE 20.3 A spontaneous oxidation-reduction reaction involving zinc and copper.