CHEMISTRY THE CENTRAL SCIENCE
21 NUCLEAR CHEMISTRY
21.6 ENERGY CHANGES IN NUCLEAR REACTIONS
The energies associated with nuclear reactions can be considered with the aid of Einstein's celebrated equation relating mass and energy:
In this equation E stands for energy, m for mass, and c for the speed of light, 2.9979 × 108 m/s. This equation states that the mass and energy of an object are proportional. If a system loses mass, it loses energy (exothermic); if it gains mass, it gains energy (endothermic). Because the proportionality constant in the equation, c2, is such a large number, even small changes in mass are accompanied by large changes in energy.
The mass changes in chemical reactions are too small to detect. For example, the mass change associated with the combustion of 1 mol of CH4 (an exothermic process) is –9.9 × 10–9 g. Because the mass change is so small, it is possible to treat chemical reactions as though mass is conserved.
The mass changes and the associated energy changes in nuclear reactions are much greater than those in chemical reactions. The mass change accompanying the radioactive decay of 1 mol of uranium-238, for example, is 50,000 times greater than that for the combustion of 1 mol of CH4. Let's examine the energy change for the nuclear reaction
The masses of the nuclei are 
, 238.0003 amu; 
, 233.9942 amu; and 
, 4.0015 amu. The mass change, Δm, is the total mass of the products minus the total mass of the reactants. The mass change for the decay of 1 mol of uranium-238 can then be expressed in grams:
The fact that the system has lost mass indicates that the process is exothermic. All spontaneous nuclear reactions are exothermic.
The energy change per mole associated with this reaction is
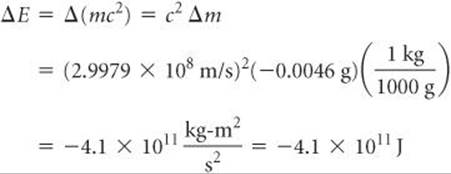
Notice that Δm must be converted to kilograms, the SI unit of mass, to obtain ΔE in joules, the SI unit of energy. The negative sign for the energy change indicates that energy is released in the reaction—in this case, over 400 billion joules per mole of uranium!
SAMPLE EXERCISE 21.9 Calculating Mass Change in a Nuclear Reaction
How much energy is lost or gained when 1 mol of cobalt-60 undergoes beta decay, 
The mass of a 
atom is 59.933819 amu, and that of a 
atom is 59.930788 amu.
SOLUTION
Analyze We are asked to calculate the energy change in a nuclear reaction.
Plan We must first calculate the mass change in the process. We are given atomic masses, but we need the masses of the nuclei in the reaction. We calculate these by taking account of the masses of the electrons that contribute to the atomic masses.
Solve A 
atom has 27 electrons. The mass of an electron is 5.4858 × 10–4 amu. (See the list of fundamental constants in the back inside cover.) We subtract the mass of the 27 electrons from the mass of the 
atom to find the mass of the 
nucleus:
59.933819 amu – (27)(5.4858 × 10–4 amu) = 59.919007 amu (or 59.919007 g/mol)
Likewise, for 
, the mass of the nucleus is
59.930788 amu – (28)(5.4858 × 10–4 amu) = 59.915428 amu (or 59.915428 g/mol)
The mass change in the nuclear reaction is the total mass of the products minus the mass of the reactant:
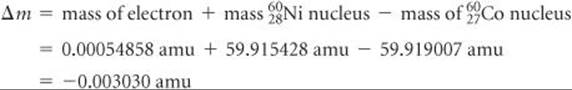
Thus, when a mole of cobalt-60 decays,
Because the mass decreases (Δm < 0), energy is released (ΔE < 0). The quantity of energy released per mole of cobalt-60 is calculated using Equation 21.22:
PRACTICE EXERCISE
Positron emission from 
, occurs with release of 2.87 × 1011 J per mole of 11C. What is the mass change per mole of 11C in this nuclear reaction? The masses of 11B and 11C are 11.009305 and 11.011434 amu, respectively.
Answer: –3.19 × 10–3 g
Nuclear Binding Energies
Scientists discovered in the 1930s that the masses of nuclei are always less than the masses of the individual nucleons of which they are composed. For example, the helium-4 nucleus has a mass of 4.00150 amu. The mass of a proton is 1.00728 amu and that of a neutron is 1.00866 amu. Consequently, two protons and two neutrons have a total mass of 4.03188 amu:
The mass of the individual nucleons is 0.03038 amu greater than that of the helium-4 nucleus:
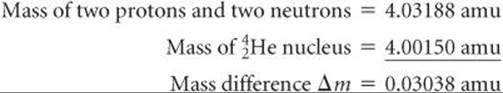
The mass difference between a nucleus and its constituent nucleons is called the mass defect. The origin of the mass defect is readily understood if we consider that energy must be added to a nucleus to break it into separated protons and neutrons:
The addition of energy to a system must be accompanied by a proportional increase in mass. The mass change we just calculated for the conversion of helium-4 into separated nucleons is Δm = 0.03038 amu. Therefore, the energy required for this process is
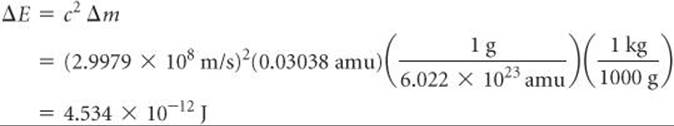
The energy required to separate a nucleus into its individual nucleons is called the nuclear binding energy. The mass defect and nuclear binding energy for three elements are compared in 
TABLE 21.7.
TABLE 21.7 • Mass Defects and Binding Energies for Three Nuclei
GIVE IT SOME THOUGHT
The atomic mass of iron-56 is 55.93494 amu. Why is this number different from the mass of the nucleus given in Table 21.7?
Values of binding energies per nucleon can be used to compare the stabilities of different combinations of nucleons (such as two protons and two neutrons arranged either as 
or as 
). 
FIGURE 21.12 shows average binding energy per nucleon plotted against mass number. Binding energy per nucleon at first increases in magnitude as mass number increases, reaching about 1.4 × 10–12 J for nuclei whose mass numbers are in the vicinity of iron-56. It then decreases slowly to about 1.2 × 10–12 J for very heavy nuclei. This trend indicates that nuclei of intermediate mass numbers are more tightly bound (and therefore more stable) than those with either smaller or larger mass numbers.
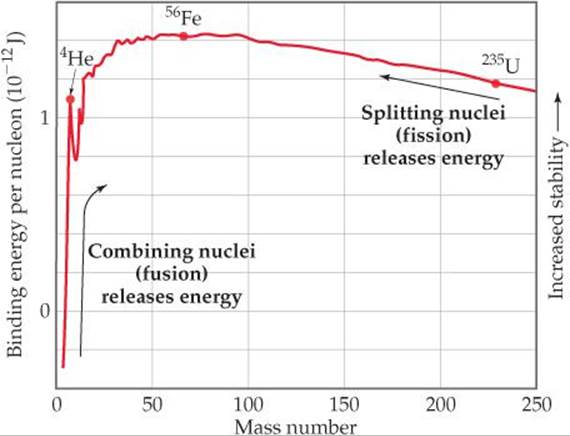
FIGURE 21.12 Nuclear binding energies. The average binding energy per nucleon increases initially as the mass number increases and then decreases slowly. Because of these trends, fusion of light nuclei and fission of heavy nuclei are exothermic processes.
This trend has two significant consequences: First, heavy nuclei gain stability and therefore give off energy if they are fragmented into two midsized nuclei. This process, known as fission, is used to generate energy in nuclear power plants. Second, even greater amounts of energy are released if very light nuclei are combined, or fused together, to give more massive nuclei. This fusion process is the essential energy-producing process in the Sun.
GIVE IT SOME THOUGHT
Could fusing two stable nuclei that have mass numbers in the vicinity of 100 be an energy-releasing process?