CHEMISTRY THE CENTRAL SCIENCE

3 STOICHIOMETRY: CALCULATIONS WITH CHEMICAL FORMULAS AND EQUATIONS

A BURNING MATCH. The heat and flame are visible evidence of a chemical reaction. Combustion reactions were among the first systematically studied chemical reactions.

WHAT'S AHEAD

3.1 CHEMICAL EQUATIONS

We begin by considering how we can use chemical formulas to write equations representing chemical reactions.

3.2 SOME SIMPLE PATTERNS OF CHEMICAL REACTIVITY

We then examine some simple chemical reactions: combination reactions, decomposition reactions, and combustion reactions.

3.3 FORMULA WEIGHTS

We see how to obtain quantitative information from chemical formulas by using formula weights.

3.4 AVOGADRO'S NUMBER AND THE MOLE

We use chemical formulas to relate the masses of substances to the numbers of atoms, molecules, or ions contained in the substances, a relationship that leads to the crucially important concept of the mole, defined as 6.022 × 10²³ objects (atoms, molecules, ions, etc.).

3.5 EMPIRICAL FORMULAS FROM ANALYSES

We apply the mole concept to determine chemical formulas from the masses of each element in a given quantity of a compound.

3.6 QUANTITATIVE INFORMATION FROM BALANCED EQUATIONS

We use the quantitative information inherent in chemical formulas and equations together with the mole concept to predict the amounts of substances consumed or produced in chemical reactions.

3.7 LIMITING REACTANTS

We recognize that one reactant may be used up before others in a chemical reaction. This is the limiting reactant. The reaction stops, leaving some excess starting material.

YOU POUR VINEGAR INTO a glass of water containing baking soda and bubbles form. You strike a match and use the flame to light a candle. You heat sugar in a pan and it turns brown. The bubbles, flame, and color change are visual evidence that something is happening. To an experienced eye, these visual changes indicate a chemical change, or chemical reaction. Some chemical changes are simple; others are complex. Some are dramatic; some are very subtle. Even as you sit reading this chapter, chemical changes are occurring in your body. Those occurring in your eyes and brain, for example, allow you to see these words and think about them. Although not as obvious as those we see in the laboratory, the chemical changes taking place in our bodies are nevertheless remarkable for how they allow us to function.

In this chapter we explore some important aspects of chemical change. Our focus will be both on the use of chemical formulas to represent reactions and on the quantitative information we can obtain about the amounts of substances involved in reactions. Stoichiometry (pronounced stoy-key-OM-uh-tree) is the area of study that examines the quantities of substances consumed and produced in chemical reactions. Stoichiometry (Greek stoicheion, “element,” and metron, “measure”) provides an essential set of tools widely used in chemistry, including such diverse applications as measuring ozone concentrations in the atmosphere and assessing different processes for converting coal into gaseous fuels.

Stoichiometry is built on an understanding of atomic masses (Section 2.4), chemical formulas, and the law of conservation of mass. (Section 2.1) The French nobleman and scientist Antoine Lavoisier (FIGURE 3.1) discovered this important chemical law during the late 1700s. Lavoisier stated the law in this eloquent way: “We may lay it down as an incontestable axiom that, in all the operations of art and nature, nothing is created; an equal quantity of matter exists both before and after the experiment. Upon this principle, the whole art of performing chemical experiments depends.” With the advent of Dalton's atomic theory, chemists came to understand the basis for this law: Atoms are neither created nor destroyed during a chemical reaction. The changes that occur during any reaction merely rearrange the atoms. The same collection of atoms is present both before and after the reaction.

FIGURE 3.1 Antoine Lavoisier (1734–1794). The science career of Lavoisier, who conducted many important studies on combustion reactions, was cut short by the French Revolution. Guillotined in 1794 during the Reign of Terror, he is generally considered the father of modern chemistry because he conducted carefully controlled experiments and used quantitative measurements.

3.1 CHEMICAL EQUATIONS

We represent chemical reactions by chemical equations. When the gas hydrogen (H₂) burns, for example, it reacts with oxygen (O₂) in the air to form water (H₂O). We write the chemical equation for this reaction as

We read the + sign as “reacts with” and the arrow as “produces.” The chemical formulas to the left of the arrow represent the starting substances, called reactants. The chemical formulas to the right of the arrow represent substances produced in the reaction, called products. The numbers in front of the formulas, called coefficients, indicate the relative numbers of molecules of each kind involved in the reaction. (As in algebraic equations, the coefficient 1 is usually not written.)

Because atoms are neither created nor destroyed in any reaction, a chemical equation must have an equal number of atoms of each element on each side of the arrow. When this condition is met, the equation is balanced. On the right side of Equation 3.1, for example, there are two molecules of H₂O, each composed of two atoms of hydrogen and one atom of oxygen (FIGURE 3.2). Thus, 2 H₂O (read “two molecules of water”) contains 2 × 2 = 4 H atoms and 2 × 1 = 2 O atoms. Notice that the number of atoms is obtained by multiplying each subscript in a chemical formula by the coefficient for the formula. Because there are four H atoms and two O atoms on each side of the equation, the equation is balanced.

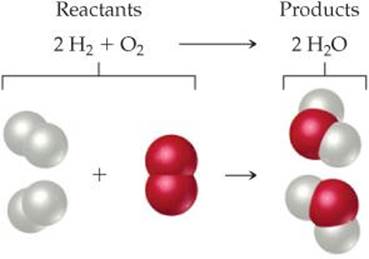
FIGURE 3.2 A balanced chemical equation.

GIVE IT SOME THOUGHT

How many atoms of Mg, O, and H are represented by the notation 3 Mg(OH)₂?

Balancing Equations

Once we know the formulas of the reactants and products in a reaction, we can write an unbalanced equation. We then balance the equation by determining the coefficients that provide equal numbers of each type of atom on the two sides of the equation. For most purposes, a balanced equation should contain the smallest possible whole-number coefficients.

GO FIGURE

What is the difference in atom count between the notation CO₂ and the notation 2 CO?

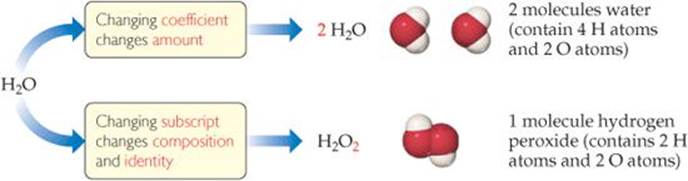
FIGURE 3.3 The difference between changing subscripts and changing coefficients in chemical equations.

In balancing an equation, you need to understand the difference between coefficients and subscripts. As FIGURE 3.3 illustrates, changing a subscript in a formula—from H₂O to H₂O₂, for example—changes the identity of the substance. The substance H₂O₂, hydrogen peroxide, is quite different from the substance H₂O, water. Never change subscripts when balancing an equation. In contrast, placing a coefficient in front of a formula changes only the amount of the substance and not its identity. Thus, 2 H₂O means two molecules of water, 3 H₂O means three molecules of water, and so forth.

To illustrate the process of balancing an equation, consider the reaction that occurs when methane (CH₄), the principal component of natural gas, burns in air to produce carbon dioxide gas (CO₂) and water vapor (H₂O) (FIGURE 3.4). Both products contain oxygen atoms that come from O₂ in the air. Thus, O₂ is a reactant, and the unbalanced equation is

It is usually best to balance first those elements that occur in the fewest chemical formulas in the equation. In our example, C appears in only one reactant (CH₄) and one product (CO₂). The same is true for H(CH₄ and H₂O). Notice, however, that O appears in one reactant (O₂) and two products (CO₂ and H₂O). So, let's begin with C. Because one molecule of CH₄ contains the same number of C atoms (one) as one molecule of CO₂ the coefficients for these substances must be the same in the balanced equation. Therefore, we start by choosing the coefficient 1 (unwritten) for both CH₄ and CO₂.

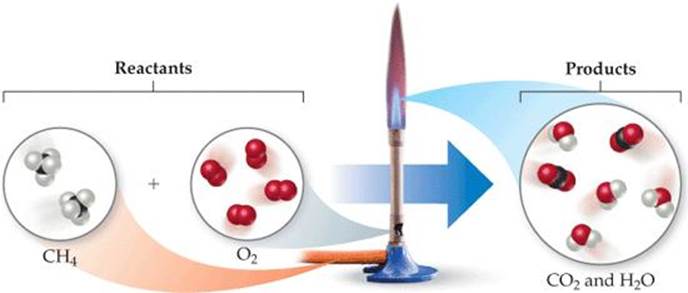
FIGURE 3.4 Methane reacts with oxygen in a Bunsen burner.

Next we focus on H. Because CH₄ contains four H atoms and H₂O contains two H atoms, we balance the H atoms by placing the coefficient 2 in front of H₂O. There are then four H atoms on each side of the equation:

Finally, a coefficient 2 in front of O₂ balances the equation by giving four O atoms on each side (2 × 2 left, 2 + 2 × 1 right):

The molecular view of the balanced equation is shown in FIGURE 3.5.

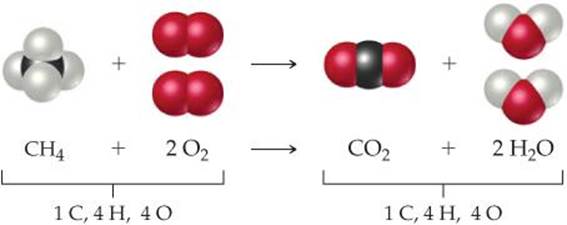
FIGURE 3.5 Balanced chemical equation for the combustion of CH₄.

SAMPLE EXERCISE 3.1 Interpreting and Balancing Chemical Equations

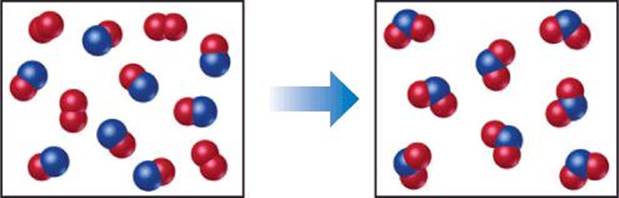
The following diagram represents a chemical reaction in which the red spheres are oxygen atoms and the blue spheres are nitrogen atoms. (a) Write the chemical formulas for the reactants and products. (b) Write a balanced equation for the reaction. (c) Is the diagram consistent with the law of conservation of mass?

SOLUTION

(a) The left box, which represents reactants, contains two kinds of molecules, those composed of two oxygen atoms (O₂) and those composed of one nitrogen atom and one oxygen atom (NO). The right box, which represents products, contains only molecules composed of one nitrogen atom and two oxygen atoms (NO₂).

(b) The unbalanced chemical equation is

An inventory of atoms on each side of the equation shows that there are one N and three O on the left side of the arrow and one N and two O on the right. To balance O we must increase the number of O atoms on the right while keeping the coefficients for NO and NO₂ equal. Sometimes we need to go back and forth several times from one side of an equation to the other, changing coefficients first on one side of the equation and then the other until it is balanced. In our present case, we can increase the number of O atoms by placing the coefficient 2 in front of NO₂:

That gives two N atoms and four O atoms on the right, so we go ba to the left side. Placing the coefficient 2 in front of NO balances both N and O:

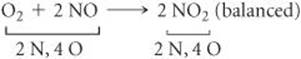
(c) The reactants box contains four O₂ and eight NO. Thus, the molecular ratio is one O₂ for each two NO, as required by the balanced equation. The products box contains eight NO₂, which means the number of NO₂ product molecules equals the number of NO reactant molecules, as the balanced equation requires.

There are eight N atoms in the eight NO molecules in the reactants box. There are also 4 × 2 = 8 O atoms in the O₂ molecules and eight O atoms in the NO molecules, giving a total of 16 O atoms. In the products box, we find eight N atoms and 8 × 2 = 16 O atoms in the eight NO₂molecules. Because there are equal numbers of N and O atoms in the two boxes, the drawing is consistent with the law of conservation of mass.

PRACTICE EXERCISE

In the following diagram, the white spheres represent hydrogen atoms and the blue spheres represent nitrogen atoms.

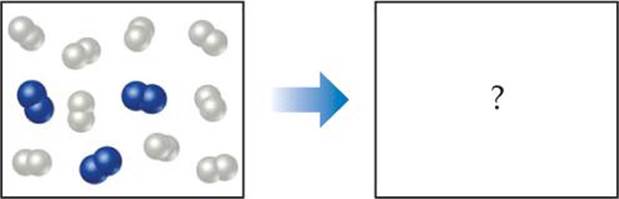
To be consistent with the law of conservation of mass, how many NH₃ molecules should be shown in the right (products) box?

Answer: Six NH₃ molecules

Indicating the States of Reactants and Products

Symbols indicating the physical state of each reactant and product are often shown in chemical equations. We use the symbols (g), (l), (s), and (aq) for gas, liquid, solid, and aqueous (water) solution, respectively. Thus, Equation 3.4 can be written

Sometimes the conditions under which the reaction proceeds appear above or below the reaction arrow. The symbol (Greek uppercase delta) above the arrow indicates addition of heat.

SAMPLE EXERCISE 3.2 Balancing Chemical Equations

Balance the equation

SOLUTION

Begin by counting each kind of atom on the two sides of the arrow. There are one Na, one O, and two H on the left side, and one Na, one O, and three H on the right. To increase the number of H atoms on the left, let's try placing the coefficient 2 in front of H₂O:

Although beginning this way does not balance H, it does increase the number of reactant H atoms, which we need to do. (Also, adding the coefficient 2 on H₂O unbalances O, but we will take care of that after we balance H.) Now that we have 2 H₂O on the left, we balance H by putting the coefficient 2 in front of NaOH:

Balancing H in this way brings O into balance, but now Na is unbalanced, with one Na on the left and two on the right. To rebalance Na, we put the coefficient 2 in front of the reactant:

We now have two Na atoms, four H atoms, and two O atoms on each side. The equation is balanced.

Comment Notice that we moved back and forth, placing a coefficient in front of H₂O, then NaOH, and finally Na. In balancing equations, we often find ourselves following this pattern of moving back and forth from one side of the arrow to the other, placing coefficients first in front of a formula on one side and then in front of a formula on the other side until the equation is balanced. You can always tell if you have balanced your equation correctly by checking that the number of atoms of each element is the same on the two sides of the arrow.

PRACTICE EXERCISE

Balance these equations by providing the missing coefficients:

Answers: (a) 4, 3, 2; (b) 1, 3, 2, 2; (c) 2, 6, 2, 3