CHEMISTRY THE CENTRAL SCIENCE
21 NUCLEAR CHEMISTRY
21.9 RADIATION IN THE ENVIRONMENT AND LIVING SYSTEMS
We are continuously bombarded by radiation from both natural and artificial sources. We are exposed to infrared, ultraviolet, and visible radiation from the Sun; radio waves from radio and television stations; microwaves from microwave ovens; X-rays from medical procedures; and radioactivity from natural materials (![]() TABLE 21.8). Understanding the different energies of these various kinds of radiation is necessary in order to understand their different effects on matter.
TABLE 21.8). Understanding the different energies of these various kinds of radiation is necessary in order to understand their different effects on matter.
When matter absorbs radiation, the radiation energy can cause atoms in the matter to be either excited or ionized. In general, radiation that causes ionization, called ionizing radiation, is far more harmful to biological systems than radiation that does not cause ionization. The latter, called nonionizing radiation, is generally of lower energy, such as radiofrequency electromagnetic radiation ![]() (Section 6.7) or slow-moving neutrons.
(Section 6.7) or slow-moving neutrons.
Most living tissue contains at least 70% water by mass. When living tissue is irradiated, water molecules absorb most of the energy of the radiation. Thus, it is common to define ionizing radiation as radiation that can ionize water, a process requiring a minimum energy of 1216 kJ/mol. Alpha, beta, and gamma rays (as well as X-rays and higher-energy ultraviolet radiation) possess energies in excess of this quantity and are therefore forms of ionizing radiation.
 A CLOSER LOOK
A CLOSER LOOK
NUCLEAR SYNTHESIS OF THE ELEMENTS
The lightest elements—hydrogen and helium along with very small amounts of lithium and beryllium—were formed as the universe expanded in the moments following the Big Bang. All the heavier elements owe their existence to nuclear reactions that occur in stars. These heavier elements are not all created equally, however. Carbon and oxygen are a million times more abundant than lithium and boron, for instance, and over 100 million times more abundant that beryllium (![]() FIGURE 21.22)! In fact, of the elements heavier than helium, carbon and oxygen are the most abundant. This is more than an academic curiosity given the fact that these elements, together with hydrogen, are the most important elements for life on Earth. Let's look at the factors responsible for the relatively high abundance of carbon and oxygen in the universe.
FIGURE 21.22)! In fact, of the elements heavier than helium, carbon and oxygen are the most abundant. This is more than an academic curiosity given the fact that these elements, together with hydrogen, are the most important elements for life on Earth. Let's look at the factors responsible for the relatively high abundance of carbon and oxygen in the universe.
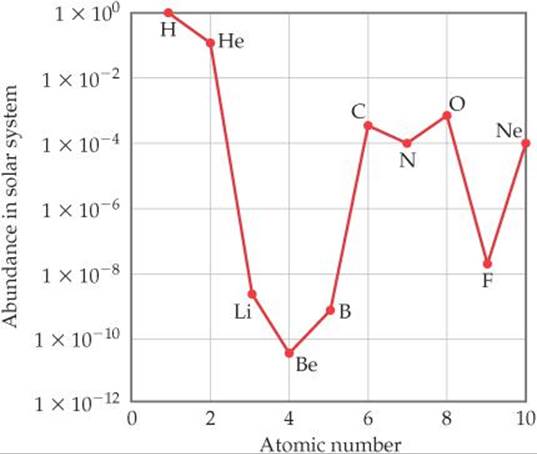
![]() FIGURE 21.22 Abundances of elements 1–10 in the solar system. Note the logarithmic scale used for the y-axis.
FIGURE 21.22 Abundances of elements 1–10 in the solar system. Note the logarithmic scale used for the y-axis.
A star is born from a cloud of gas and dust called a nebula. When conditions are right, gravitational forces collapse the cloud, and its core density and temperature rise until nuclear fusion commences. Hydrogen nuclei fuse to form deuterium, 2H, and eventually 4He through the reactions shown in Equations 21.26 through 21.29. Because 4He has a larger binding energy than any of its immediate neighbors (Figure 21.12), these reactions release an enormous amount of energy. This process, called hydrogen burning, is the dominant process for most of a star's lifetime.
Once a star's supply of hydrogen is nearly exhausted, several important changes occur as the star enters the red giant phase of its life. The decrease in nuclear fusion causes the core to contract, triggering an increase in core temperature and pressure. At the same time, the outer regions expand and cool enough to make the star emit red light (thus, the name red giant). The star now must use ![]() He nuclei as its fuel. The simplest reaction that can occur in the He-rich core, fusion of two alpha particles to form a
He nuclei as its fuel. The simplest reaction that can occur in the He-rich core, fusion of two alpha particles to form a ![]() Be nucleus, does occur. However, this nucleus is highly unstable (half-life of 7 × 10–17 s) and so falls apart almost immediately. In a tiny fraction of cases, however, a third
Be nucleus, does occur. However, this nucleus is highly unstable (half-life of 7 × 10–17 s) and so falls apart almost immediately. In a tiny fraction of cases, however, a third ![]() He collides with a
He collides with a ![]() Be nucleus before it decays, forming carbon-12 through the triple-alpha process:
Be nucleus before it decays, forming carbon-12 through the triple-alpha process:

Some of the ![]() nuclei go on to react with alpha particles to form oxygen-16:
nuclei go on to react with alpha particles to form oxygen-16:
![]()
This stage of nuclear fusion is called helium burning. Notice that carbon, element 6, is formed without prior formation of elements 3, 4, and 5, explaining in part their unusually low abundance. Nitrogen is relatively abundant because it can be produced from carbon through a series of reactions involving proton capture and positron emission.
Most stars gradually cool and dim as the helium is converted to carbon and oxygen, ending their lives as white dwarfs. In stars that are 10 or more times more massive than our Sun, however, a more dramatic fate awaits. The extreme mass of these stars leads to much higher temperatures and pressures at the core, where a variety of fusion processes lead to synthesis of the elements from neon to sulfur. These fusion reactions are collectively called advanced burning.
Eventually progressively heavier elements form at the core until it becomes predominantly 56Fe as shown in ![]() FIGURE 21.23. Because this is such a stable nucleus, further fusion to heavier nuclei consumes energy rather than releasing it. When this happens, the fusion reactions that power the star diminish, and immense gravitational forces lead to a dramatic collapse called a supernova explosion. Neutron capture coupled with subsequent radioactive decays in the dying moments of such a star are responsible for the presence of all elements heavier than iron and nickel.
FIGURE 21.23. Because this is such a stable nucleus, further fusion to heavier nuclei consumes energy rather than releasing it. When this happens, the fusion reactions that power the star diminish, and immense gravitational forces lead to a dramatic collapse called a supernova explosion. Neutron capture coupled with subsequent radioactive decays in the dying moments of such a star are responsible for the presence of all elements heavier than iron and nickel.
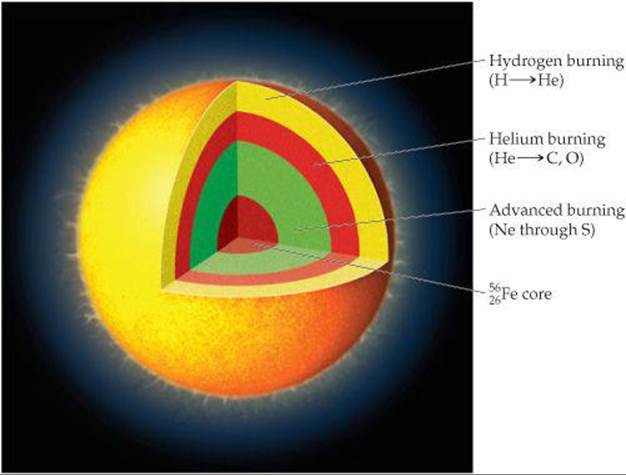
![]() FIGURE 21.23 Fusion processes going on in a red giant just prior to a supernova explosion.
FIGURE 21.23 Fusion processes going on in a red giant just prior to a supernova explosion.
Without these dramatic supernova events, heavier elements that are so familiar to us, such as silver, gold, iodine, lead, and uranium, would not exist.
RELATED EXERCISES: 21.70, 21.72
TABLE 21.8 • Average Abundances and Activities of Natural Radionuclides*

When ionizing radiation passes through living tissue, electrons are removed from water molecules, forming highly reactive H2O+ ions. An H2O+ ion can react with another water molecule to form an H3O+ ion and a neutral OH molecule:
![]()
The unstable and highly reactive OH molecule is a free radical, a substance with one or more unpaired electrons, as seen in the Lewis structure ·![]() —H. The OH molecule is also called the hydroxyl radical, and the presence of the unpaired electron is often emphasized by writing the species with a single dot, · OH. In cells and tissues, hydroxyl radicals can attack biomolecules to produce new free radicals, which in turn attack yet other biomolecules. Thus, the formation of a single hydroxyl radical via Equation 21.31 can initiate a large number of chemical reactions that are ultimately able to disrupt the normal operations of cells.
—H. The OH molecule is also called the hydroxyl radical, and the presence of the unpaired electron is often emphasized by writing the species with a single dot, · OH. In cells and tissues, hydroxyl radicals can attack biomolecules to produce new free radicals, which in turn attack yet other biomolecules. Thus, the formation of a single hydroxyl radical via Equation 21.31 can initiate a large number of chemical reactions that are ultimately able to disrupt the normal operations of cells.
The damage produced by radiation depends on the activity and energy of the radiation, the length of exposure, and whether the source is inside or outside the body. Gamma rays are particularly harmful outside the body because they penetrate human tissue very effectively, just as X-rays do. Consequently, their damage is not limited to the skin. In contrast, most alpha rays are stopped by skin, and beta rays are able to penetrate only about 1 cm beyond the skin surface (![]() FIGURE 21.24). Neither alpha rays nor beta rays are as dangerous as gamma rays, therefore, unless the radiation source somehow enters the body. Within the body, alpha rays are particularly dangerous because they transfer their energy efficiently to the surrounding tissue, causing considerable damage.
FIGURE 21.24). Neither alpha rays nor beta rays are as dangerous as gamma rays, therefore, unless the radiation source somehow enters the body. Within the body, alpha rays are particularly dangerous because they transfer their energy efficiently to the surrounding tissue, causing considerable damage.
![]() GO FIGURE
GO FIGURE
Why are alpha rays much more dangerous when the source of radiation is located inside the body?
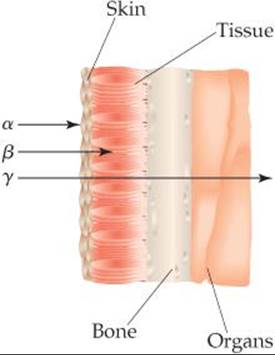
![]() FIGURE 21.24 Relative penetrating abilities of alpha, beta, and gamma radiation.
FIGURE 21.24 Relative penetrating abilities of alpha, beta, and gamma radiation.
In general, the tissues damaged most by radiation are those that reproduce rapidly, such as bone marrow, blood-forming tissues, and lymph nodes. The principal effect of extended exposure to low doses of radiation is to cause cancer. Cancer is caused by damage to the growth-regulation mechanism of cells, inducing the cells to reproduce uncontrollably. Leukemia, which is characterized by excessive growth of white blood cells, is probably the major type of radiation-caused cancer.
In light of the biological effects of radiation, it is important to determine whether any levels of exposure are safe. Unfortunately, we are hampered in our attempts to set realistic standards because we do not fully understand the effects of long-term exposure. Scientists concerned with setting health standards have used the hypothesis that the effects of radiation are proportional to exposure. Any amount of radiation is assumed to cause some finite risk of injury, and the effects of high dosage rates are extrapolated to those of lower ones. Other scientists believe, however, that there is a threshold below which there are no radiation risks. Until scientific evidence enables us to settle the matter with some confidence, it is safer to assume that even low levels of radiation present some danger.
Radiation Doses
Two units are commonly used to measure exposure to radiation. The gray (Gy), the SI unit of absorbed dose, corresponds to the absorption of 1 J of energy per kilogram of tissue. The rad (radiation absorbed dose) corresponds to the absorption of 1 × 10–2 J of energy per kilogram of tissue. Thus, 1 Gy = 100 rad. The rad is the unit most often used in medicine.
Not all forms of radiation harm biological materials with the same efficiency. For example, 1 rad of alpha radiation can produce more damage than 1 rad of beta radiation. To correct for these differences, the radiation dose is multiplied by a factor that measures the relative damage caused by the radiation. This multiplication factor is known as the relative biological effectiveness, RBE. The RBE is approximately 1 for gamma and beta radiation, and 10 for alpha radiation.
The exact value of the RBE varies with dose rate, total dose, and type of tissue affected. The product of the radiation dose in rads and the RBE of the radiation give the effective dosage in rem (roentgen equivalent for man):
![]()
The SI unit for effective dose is the sievert (Sv), obtained by multiplying the RBE times the SI unit for radiation dose, the gray; because a gray is 100 times larger than a rad, 1Sv = 100 rem. The rem is the unit of radiation damage usually used in medicine.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
If a 50-kg person is uniformly irradiated by 0.10-J alpha radiation, what is the absorbed dosage in rad and the effective dosage in rem?
The effects of short-term exposure to radiation appear in ![]() TABLE 21.9. An exposure of 600 rem is fatal to most humans. To put this number in perspective, a typical dental X-ray entails an exposure of about 0.5 mrem. The average exposure for a person in 1 year due to all natural sources of ionizing radiation (called background radiation) is about 360 mrem (
TABLE 21.9. An exposure of 600 rem is fatal to most humans. To put this number in perspective, a typical dental X-ray entails an exposure of about 0.5 mrem. The average exposure for a person in 1 year due to all natural sources of ionizing radiation (called background radiation) is about 360 mrem (![]() FIGURE 21.25).
FIGURE 21.25).
TABLE 21.9 • Effects of Short-Term Exposures to Radiation

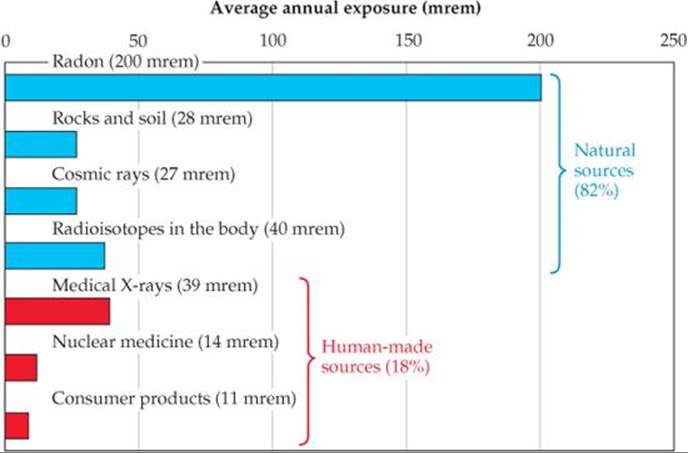
![]() FIGURE 21.25 Sources of U.S. average annual exposure to high-energy radiation. The total average annual exposure is 360 mrem. Data from “Ionizing Radiation Exposure of the Population of the United States,” Report 93, 1987, National Council on Radiation Protection.
FIGURE 21.25 Sources of U.S. average annual exposure to high-energy radiation. The total average annual exposure is 360 mrem. Data from “Ionizing Radiation Exposure of the Population of the United States,” Report 93, 1987, National Council on Radiation Protection.
Radon
Radon-222 is a product of the nuclear disintegration series of uranium-238 (Figure 21.3) and is continuously generated as uranium in rocks and soil decays. As Figure 21.25 indicates, radon exposure is estimated to account for more than half the 360-mrem average annual exposure to ionizing radiation.
The interplay between the chemical and nuclear properties of radon makes it a health hazard. Because radon is a noble gas, it is extremely unreactive and is therefore free to escape from the ground without chemically reacting along the way. It is readily inhaled and exhaled with no direct chemical effects. Its half-life, however, is only 3.82 days. It decays, by losing an alpha particle, into a radioisotope of polonium:
![]()
Because radon has such a short half-life and because alpha particles have a high RBE, inhaled radon is considered a probable cause of lung cancer. Even worse than the radon, however, is the decay product because polonium-218 is an alpha-emitting chemically active element that has an even shorter half-life (3.11 min) than radon-222:
![]()
When a person inhales radon, therefore, atoms of polonium-218 can become trapped in the lungs, where they bathe the delicate tissue with harmful alpha radiation. The resulting damage is estimated to contribute to 10% of all lung cancer deaths in the United States.
The U.S. Environmental Protection Agency (EPA) has recommended that radon-222 levels not exceed 4 pCi per liter of air in homes. Homes located in areas where the natural uranium content of the soil is high often have levels much greater than that (![]() FIGURE 21.26). Because of public awareness, radon-testing kits are readily available in many parts of the country.
FIGURE 21.26). Because of public awareness, radon-testing kits are readily available in many parts of the country.
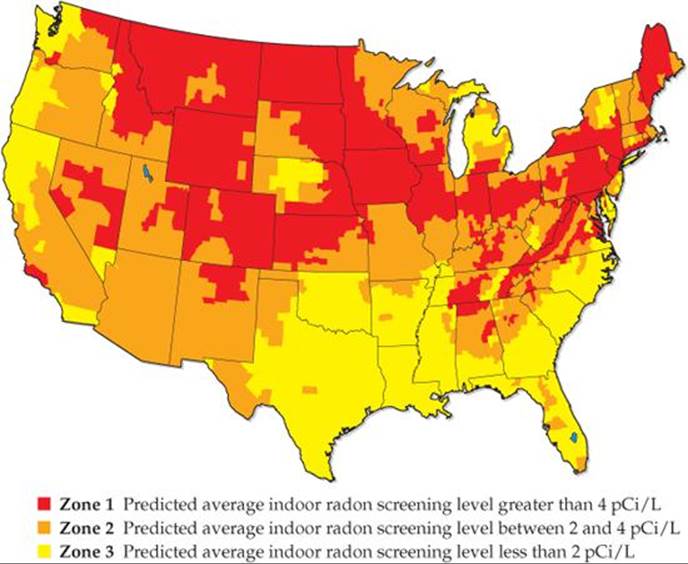
![]() FIGURE 21.26 EPA map of radon zones in the United States. The color coding shows average indoor radon levels as a function of geographic location.
FIGURE 21.26 EPA map of radon zones in the United States. The color coding shows average indoor radon levels as a function of geographic location.
 CHEMISTRY AND LIFE
CHEMISTRY AND LIFE
RADIATION THERAPY
Healthy cells are either destroyed or damaged by high-energy radiation, leading to physiological disorders. This radiation can also destroy unhealthy cells, however, including cancerous cells. All cancers are characterized by runaway cell growth that can produce malignant tumors. These tumors can be caused by the exposure of healthy cells to high-energy radiation. Paradoxically, however, they can be destroyed by the same radiation that caused them because the rapidly reproducing cells of the tumors are very susceptible to radiation damage. Thus, cancerous cells are more susceptible to destruction by radiation than healthy ones, allowing radiation to be used effectively in the treatment of cancer. As early as 1904, physicians used the radiation emitted by radioactive substances to treat tumors by destroying the mass of unhealthy tissue. The treatment of disease by high-energy radiation is called radiation therapy.
Many radionuclides are currently used in radiation therapy. Most of them have short half-lives, meaning that they emit a great deal of radiation in a short period of time (![]() TABLE 21.10).
TABLE 21.10).
TABLE 21.10 • Some Radioisotopes Used in Radiation Therapy
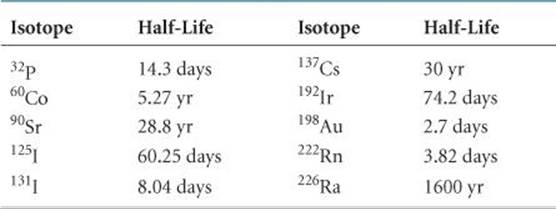
The radiation source used in radiation therapy may be inside or outside the body. In almost all cases, radiation therapy uses gamma radiation emitted by radioisotopes. Any alpha or beta radiation that is emitted concurrently can be blocked by appropriate packaging. For example, 192Ir is often administered as “seeds” consisting of a core of radioactive isotope coated with 0.1 mm of platinum metal. The platinum coating stops the alpha and beta rays, but the gamma rays penetrate it readily. The radioactive seeds can be surgically implanted in a tumor.
In some cases, human physiology allows a radioisotope to be ingested. For example, most of the iodine in the human body ends up in the thyroid gland, so thyroid cancer can be treated by using large doses of 131I. Radiation therapy on deep organs, where a surgical implant is impractical, often uses a 60Co “gun” outside the body to shoot a beam of gamma rays at the tumor. Particle accelerators are also used as an external source of high-energy radiation for radiation therapy.
Because gamma radiation is so strongly penetrating, it is nearly impossible to avoid damaging healthy cells during radiation therapy. Many cancer patients undergoing radiation treatment experience unpleasant and dangerous side effects such as fatigue, nausea, hair loss, a weakened immune system, and occasionally even death. However, if other treatments such as chemotherapy (the use of drugs to combat cancer) fail, radiation therapy can be a good option.
SAMPLE INTEGRATIVE EXERCISE Putting Concepts Together
Potassium ion is present in foods and is an essential nutrient in the human body. One of the naturally occurring isotopes of potassium, potassium-40, is radioactive. Potassium-40 has a natural abundance of 0.0117% and a half-life t1/2 = 1.28 × 109 yr. It undergoes radioactive decay in three ways: 98.2% is by electron capture, 1.35% is by beta emission, and 0.49% is by positron emission. (a) Why should we expect 40K to be radioactive? (b) Write the nuclear equations for the three modes by which 40K decays. (c) How many 40K+ ions are present in 1.00 g of KCl? (d) How long does it take for 1.00% of the 40K in a sample to undergo radioactive decay?
SOLUTION
(a) The 40K nucleus contains 19 protons and 21 neutrons. There are very few stable nuclei with odd numbers of both protons and neutrons (Section 21.2).
(b) Electron capture is capture of an inner-shell electron by the nucleus:
![]()
Beta emission is loss of a beta particle ![]() by the nucleus:
by the nucleus:
![]()
Positron emission is loss of a positron ![]() by the nucleus:
by the nucleus:
![]()
(c) The total number of K+ ions in the sample is
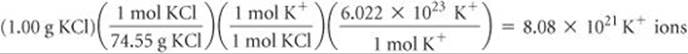
Of these, 0.0117% are 40K+ ions:
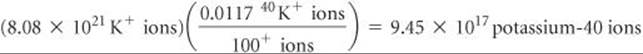
(d) The decay constant (the rate constant) for the radioactive decay can be calculated from the half-life, using Equation 21.20:
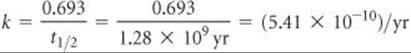
The rate equation, Equation 21.19, then allows us to calculate the time required:
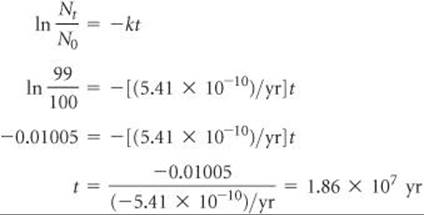
That is, it would take 18.6 million years for just 1.00% of the 40K in a sample to decay.