CHEMISTRY THE CENTRAL SCIENCE
3 STOICHIOMETRY: CALCULATIONS WITH CHEMICAL FORMULAS AND EQUATIONS
3.3 FORMULA WEIGHTS
Chemical formulas and chemical equations both have a quantitative significance in that the subscripts in formulas and the coefficients in equations represent precise quantities. The formula H2O indicates that a molecule of this substance (water) contains exactly two atoms of hydrogen and one atom of oxygen. Similarly, the coefficients in a balanced chemical equation indicate the relative quantities of reactants and products. But how do we relate the numbers of atoms or molecules to the amounts we measure in the laboratory? Although we cannot directly count atoms or molecules, we can indirectly determine their numbers if we know their masses. Therefore, before we can pursue the quantitative aspects of chemical formulas and equations, we must examine the masses of atoms and molecules.
Formula and Molecular Weights
The formula weight of a substance is the sum of the atomic weights of the atoms in the chemical formula of the substance. Using atomic weights, we find, for example, that the formula weight of sulfuric acid (H2SO4) is 98.1 amu:*
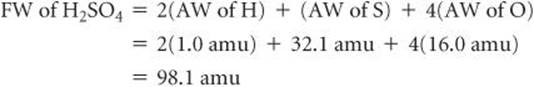
For convenience, we have rounded off the atomic weights to one decimal place, a practice we will follow in most calculations in this book.
If the chemical formula is the chemical symbol of an element, such as Na, the formula weight equals the atomic weight of the element, in this case 23.0 amu. If the chemical formula is that of a molecule, the formula weight is also called the molecular weight. The molecular weight of glucose (C6H12O6), for example, is
MW of C6H12O6 = 6(12.0 amu) + 12(1.0 amu) + 6(16.0 amu) = 180.0 amu
Because ionic substances exist as three-dimensional arrays of ions (see Figure 2.21), it is inappropriate to speak of molecules of these substances. Instead, we speak of formula units. The formula unit of NaCl, for instance, consists of one Na+ ion and one Cl− ion. Thus, the formula weight of NaCl is defined as the mass of one formula unit:
FW of NaCl = 23.0 amu + 35.5 amu = 58.5 amu
SAMPLE EXERCISE 3.5 Calculating Formula Weights
Calculate the formula weight of (a) sucrose, C12H22O11 (table sugar), and (b) calcium nitrate, Ca(NO3)2.
SOLUTION

PRACTICE EXERCISE
Calculate the formula weight of (a) Al(OH)3 and (b) CH3OH.
Answers: (a) 78.0 amu, (b) 32.0 amu
Percentage Composition from Chemical Formulas
Chemists must sometimes calculate the percentage composition of a compound—that is, the percentage by mass contributed by each element in the substance. Forensic chemists, for example, will measure the percentage composition of an unknown powder and compare it with the percentage compositions for sugar, salt, or cocaine to identify the powder.
Calculating the percentage composition of any element in a substance is straightforward if the chemical formula is known. The calculation depends on the formula weight of the substance, the atomic weight of the element of interest, and the number of atoms of that element in the chemical formula:

SAMPLE EXERCISE 3.6 Calculating Percentage Composition
Calculate the percentage of carbon, hydrogen, and oxygen (by mass) in C12H22O11.
SOLUTION
Let's examine this question using the problem-solving steps in the accompanying “Strategies in Chemistry: Problem Solving” essay.
Analyze We are given a chemical formula and asked to calculate the percentage by mass of each element.
Plan We use Equation 3.10, obtaining our atomic weights from a periodic table. We know the denominator in Equation 3.10, the formula weight of C12H22O11, from Sample Exercise 3.5. We must use that value in three calculations, one for each element.
Solve
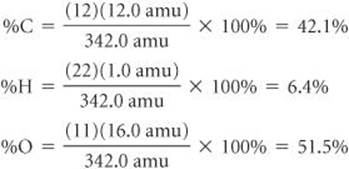
Check Our calculated percentages must add up to 100%, which they do. We could have used more significant figures for our atomic weights, giving more significant figures for our percentage composition, but we have adhered to our suggested guideline of rounding atomic weights to one digit beyond the decimal point.
PRACTICE EXERCISE
Calculate the percentage of nitrogen, by mass, in Ca(NO3)2.
Answer: 17.1%