CHEMISTRY THE CENTRAL SCIENCE
5 THERMOCHEMISTRY
5.3 ENTHALPY
The chemical and physical changes that occur around us, such as photosynthesis in the leaves of a plant, evaporation of water from a lake, or a reaction in an open beaker in a laboratory, occur under the essentially constant pressure of Earth's atmosphere.* These changes can result in the release or absorption of heat and can be accompanied by work done by or on the system. In exploring these changes, we have a number of experimental means to measure the flow of heat into and out of the system, and we therefore focus much of our discussion on what we can learn from the heat flow. (Of course, in order to apply the first law of thermodynamics to these processes, we still need to account for any work that accompanies the process.)
A system that consists of a gas confined to a container can be characterized by several different properties. Among the most important are the pressure of the gas, P, and the volume of the container, V. Like internal energy E, both P and V are state functions—they depend only on the current state of the system and not on the path taken to that state.
We can combine these three state functions—E, P, and V—to define a new state function called enthalpy (from the Greek enthalpein, “to warm”). This new function is particularly useful for discussing heat flow in processes that occur under constant (or nearly constant) pressure. Enthalpy, which we denote by the symbol H, is defined as the internal energy plus the product of the pressure and volume of the system:
GIVE IT SOME THOUGHT
Given the definition of enthalpy in Equation 5.6, why must H be a state function?
You might be asking yourself why it is convenient to define a new function H. To answer that question, recall from Equation 5.5 that ΔE involves not only the heat q added to or removed from the system but also the work w done by or on the system. Most commonly, the only kind of work produced by chemical or physical changes open to the atmosphere is the mechanical work associated with a change in volume. For example, when the reaction of zinc metal with hydrochloric acid solution, is run at constant pressure in the apparatus illustrated in 
FIGURE 5.11, the piston moves up or down to maintain a constant pressure in the vessel. If we assume for simplicity that the piston has no mass, the pressure in the apparatus is the same as atmospheric pressure. As the reaction proceeds, H2 gas forms, and the piston rises. The gas within the flask is thus doing work on the surroundings by lifting the piston against the force of atmospheric pressure.
GO FIGURE
If the amount of zinc used in the reaction is increased, will more work be done by the system? Is there additional information you need in order to answer this question?
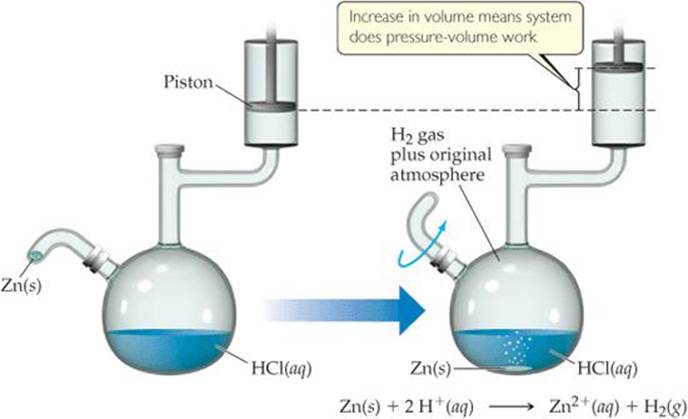
FIGURE 5.11 A system that does work on its surroundings.
The work involved in the expansion or compression of gases is called pressure–volume work (or P-V work). When pressure is constant in a process, as in our preceding example, the sign and magnitude of the pressure-volume work are given by
where P is pressure and Δ V = Vfinal— Vinitial is the change in volume of the system. The negative sign in Equation 5.8 is necessary to conform to the sign conventions of Table 5.1. The pressure P is always either a positive number or zero. If the volume of the system expands, then Δ V is positive as well. Because the expanding system does work on the surroundings, w is negative—energy leaves the system as work. Notice that if the gas is compressed, Δ V is negative (the volume decreases), and Equation 5.8 indicates that w is positive, meaning work is done on the system by the surroundings. The “A Closer Look” box discusses pressure-volume work in detail, but all you need to keep in mind for now is Equation 5.8, which applies to processes occurring at constant pressure.
GIVE IT SOME THOUGHT
If a system does not change its volume during the course of a process, does it do pressure-volume work?
Let's now return to our discussion of enthalpy. When a change occurs at constant pressure, the change in enthalpy, ΔH, is given by the relationship
That is, the change in enthalpy equals the change in internal energy plus the product of the constant pressure times the change in volume.
Recall that ΔE = q + w (Equation 5.5) and that the work involved in the expansion or compression of a gas is w = −P ΔV (at constant pressure). Substituting — w for P ΔV and q + w for ΔE into Equation 5.9, we have
The subscript P on q indicates that the process occurs at constant pressure. Thus, the change in enthalpy equals the heat qP gained or lost at constant pressure. Because qP is something we can either measure or readily calculate and because so many physical and chemical changes of interest to us occur at constant pressure, enthalpy is a more useful function for most reactions than is internal energy. In addition, for most reactions the difference in ΔH and ΔE is small because P Δ V is small.
When ΔH is positive (that is, when qP is positive), the system has gained heat from the surroundings (Table 5.1), which means the process is endothermic. When ΔH is negative, the system has released heat to the surroundings, which means the process is exothermic. To continue the bank analogy of Figure 5.7, under constant pressure an endothermic process deposits energy in the system in the form of heat and an exothermic process withdraws energy in the form of heat (
FIGURE 5.12).
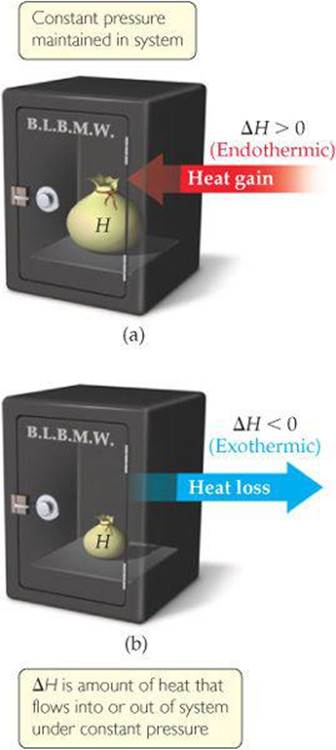
FIGURE 5.12 Endothermic and exothermic processes. (a) An endothermic process (ΔH > 0) deposits heat into the system. (b) An exothermic process (ΔH < 0) withdraws heat from the system.
Because H is a state function, ΔH (which equals qP) depends only on the initial and final states of the system, not on how the change occurs. At first glance this statement might seem to contradict our discussion in Section 5.2, in which we said that q is not a state function. There is no contradiction, however, because the relationship between ΔH and qP has the special limitations that only P-V work is involved and that the pressure is constant.
GIVE IT SOME THOUGHT
What common laboratory measuring device will we likely always use in experiments that measure enthalpy changes?
SAMPLE EXERCISE 5.3 Determining the Sign of ΔH
Indicate the sign of the enthalpy change, ΔH, in these processes carried out under atmospheric pressure and indicate whether each process is endothermic or exothermic: (a) An ice cube melts; (b) 1 g of butane (C4H10) is combusted in sufficient oxygen to give complete combustion to CO2and H2O.
SOLUTION
Analyze Our goal is to determine whether ΔH is positive or negative for each process. Because each process occurs at constant pressure, the enthalpy change equals the quantity of heat absorbed or released, ΔH = qP.
Plan We must predict whether heat is absorbed or released by the system in each process. Processes in which heat is absorbed are endothermic and have a positive sign for ΔH; those in which heat is released are exothermic and have a negative sign for ΔH.
Solve In (a) the water that makes up the ice cube is the system. The ice cube absorbs heat from the surroundings as it melts, so ΔH is positive and the process is endothermic. In (b) the system is the 1 g of butane and the oxygen required to combust it. The combustion of butane in oxygen gives off heat, so ΔH is negative and the process is exothermic.
PRACTICE EXERCISE
Molten gold poured into a mold solidifies at atmospheric pressure. With the gold defined as the system, is the solidification an exothermic or endothermic process?
Answer: In order to solidify, the gold must cool to below its melting temperature. It cools by transferring heat to its surroundings. The air around the sample would feel hot because heat is transferred to it from the molten gold, meaning the process is exothermic.
You may notice that solidification of a liquid is the reverse of the melting we analyzed in the exercise. As we will see, reversing the direction of a process changes the sign of the heat transferred.
A Closer Look
ENERGY, ENTHALPY, AND P-V WORK
In chemistry we are interested mainly in two types of work: electrical work and mechanical work done by expanding gases. We focus here on the latter, called pressure-volume, or P-V, work. Expanding gases in the cylinder of an automobile engine do P-V work on the piston; this work eventually turns the wheels. Expanding gases from an open reaction vessel do P-V work on the atmosphere. This work accomplishes nothing in a practical sense, but we must keep track of all work, useful or not, when monitoring energy changes in a system.
Let's consider a gas confined to a cylinder with a movable piston of cross-sectional area A (
FIGURE 5.13). A downward force E acts on the piston. The pressure, P, on the gas is the force per area: P = F/A. We assume that the piston is massless and that the only pressure acting on it is the atmospheric pressure that is due to Earth's atmosphere, which we assume to be constant.
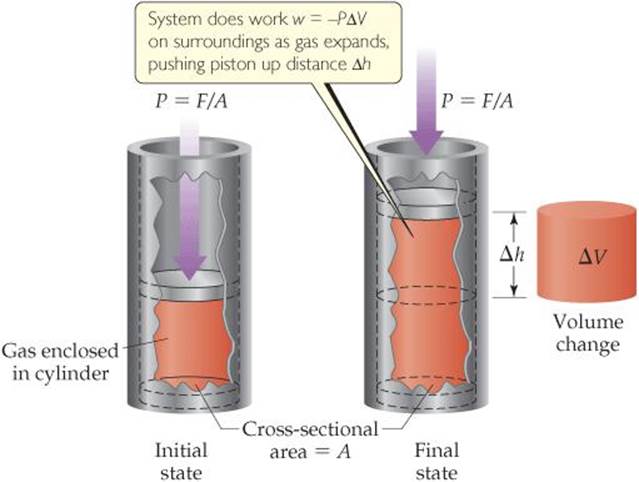
FIGURE 5.13 Pressure-volume work. The amount of work done by the system on the surroundings is w = −PΔV
Suppose the gas expands and the piston moves a distance Mi. From Equation 5.3, the magnitude of the work done by the system is
Magnitude of work = force × distance = F × h [5.11]
We can rearrange the definition of pressure, P = F/A, to F = P × A. The volume change, A V, resulting from the movement of the piston is the product of the cross-sectional area of the piston and the distance it moves: A V = A × M. Substituting into Equation 5.11 gives
Because the system (the confined gas) does work on the surroundings, the work is a negative quantity:
Now, if P-V work is the only work that can be done, we can substitute Equation 5.12 into Equation 5.5 to give
When a reaction is carried out in a constant-volume container (ΔV = 0), therefore, the heat transferred equals the change in internal energy:
The subscript V indicates that the volume is constant.
Most reactions are run under constant pressure, so that Equation 5.13 becomes
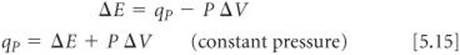
We see from Equation 5.9 that the right side of Equation 5.15 is the enthalpy change under constant-pressure conditions. Thus, ΔH = qp, as we saw in Equation 5.10.
In summary, the change in internal energy is equal to the heat gained or lost at constant volume, and the change in enthalpy is equal to the heat gained or lost at constant pressure. The difference between ΔE and ΔH is the amount of P-V work done by the system when the process occurs at constant pressure, –P AV. The volume change accompanying many reactions is close to zero, which makes P W and, therefore, the difference between ΔE and ΔH small. Under most circumstances, it is generally satisfactory to use ΔH as the measure of energy changes during most chemical processes.
RELATED EXERCISES: 5.35, 5.36, 5.37, 5.38