CHEMISTRY THE CENTRAL SCIENCE
6 ELECTRONIC STRUCTURE OF ATOMS
6.2 QUANTIZED ENERGY AND PHOTONS
Although the wave model of light explains many aspects of its behavior, this model cannot explain several phenomena. Three of these are particularly pertinent to our understanding of how electromagnetic radiation and atoms interact: (1) the emission of light from hot objects (referred to asblackbody radiation because the objects studied appear black before heating), (2) the emission of electrons from metal surfaces on which light shines (the photoelectric effect), and (3) the emission of light from electronically excited gas atoms (emission spectra). We examine the first two phenomena here and the third in Section 6.3.
Hot Objects and the Quantization of Energy
When solids are heated, they emit radiation, as seen in the red glow of an electric stove burner or the bright white light of a tungsten lightbulb. The wavelength distribution of the radiation depends on temperature; a red-hot object, for instance, is cooler than a yellowish or white-hot one (![]() FIGURE 6.5). During the late 1800s, a number of physicists studied this phenomenon, trying to understand the relationship between the temperature and the intensity and wavelength of the emitted radiation. The prevailing laws of physics could not account for the observations.
FIGURE 6.5). During the late 1800s, a number of physicists studied this phenomenon, trying to understand the relationship between the temperature and the intensity and wavelength of the emitted radiation. The prevailing laws of physics could not account for the observations.
In 1900 a German physicist named Max Planck (1858-1947) solved the problem by assuming that energy can be either released or absorbed by atoms only in discrete “chunks” of some minimum size. Planck gave the name quantum (meaning “fixed amount”) to the smallest quantity of energy that can be emitted or absorbed as electromagnetic radiation. He proposed that the energy, E, of a single quantum equals a constant times the frequency of the radiation:
![]()
![]() GO FIGURE
GO FIGURE
Which area in the photograph corresponds to the highest temperature?

![]() FIGURE 6.5 Color and temperature. The color and intensity of the light emitted by a hot object, such as this pour of molten steel, depend on the temperature of the object.
FIGURE 6.5 Color and temperature. The color and intensity of the light emitted by a hot object, such as this pour of molten steel, depend on the temperature of the object.
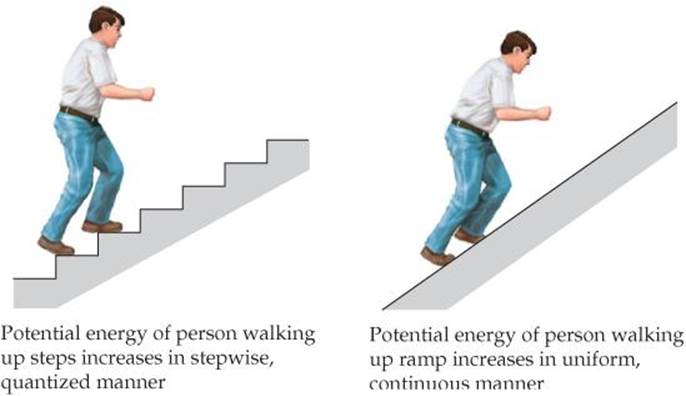
![]() FIGURE 6.6 Quantized versus continuous change in energy.
FIGURE 6.6 Quantized versus continuous change in energy.
The constant h is called Planck's constant and has a value of 6.626 × 10–34 joule-second (J-s).
According to Planck's theory, matter can emit and absorb energy only in whole-number multiples of hv, such as hv, 2hv, 3hv, and so forth. If the quantity of energy emitted by an atom is 3hv, for example, we say that three quanta of energy have been emitted (quanta being the plural ofquantum). Because the energy can be released only in specific amounts, we say that the allowed energies are quantized—their values are restricted to certain quantities. Planck's revolutionary proposal that energy is quantized was proved correct, and he was awarded the 1918 Nobel Prize in Physics for his work on the quantum theory.
If the notion of quantized energies seems strange, it might be helpful to draw an analogy by comparing a ramp and a staircase (![]() FIGURE 6.6). As you walk up a ramp, your potential energy increases in a uniform, continuous manner. When you climb a staircase, you can step only onindividual stairs, not between them, so that your potential energy is restricted to certain values and is therefore quantized.
FIGURE 6.6). As you walk up a ramp, your potential energy increases in a uniform, continuous manner. When you climb a staircase, you can step only onindividual stairs, not between them, so that your potential energy is restricted to certain values and is therefore quantized.
If Planck's quantum theory is correct, why are its effects not obvious in our daily lives? Why do energy changes seem continuous rather than quantized, or “jagged”? Notice that Planck's constant is an extremely small number. Thus, a quantum of energy, hv, is an extremely small amount. Planck's rules regarding the gain or loss of energy are always the same, whether we are concerned with objects on the scale of our ordinary experience or with microscopic objects. With everyday objects, however, the gain or loss of a single quantum of energy is so small that it goes completely unnoticed. In contrast, when dealing with matter at the atomic level, the impact of quantized energies is far more significant.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Calculate the energy (to one significant figure) of one quantum of electromagnetic radiation whose frequency is 5 × 10–3 s–1. Can this radiation produce a burst of energy E = 5 × 10–36 J? Why or why not?
The Photoelectric Effect and Photons
A few years after Planck presented his quantum theory, scientists began to see its applicability to many experimental observations. In 1905, Albert Einstein (1879-1955) used Planck's theory to explain the photoelectric effect (![]() FIGURE 6.7). Light shining on a clean metal surface causes the surface to emit electrons. A minimum frequency of light, different for different metals, is required for the emission of electrons. For example, light with a frequency of 4.60 × 1014 s–1or greater causes cesium metal to emit electrons, but light of lower frequency has no effect.
FIGURE 6.7). Light shining on a clean metal surface causes the surface to emit electrons. A minimum frequency of light, different for different metals, is required for the emission of electrons. For example, light with a frequency of 4.60 × 1014 s–1or greater causes cesium metal to emit electrons, but light of lower frequency has no effect.
To explain the photoelectric effect, Einstein assumed that the radiant energy striking the metal surface behaves like a stream of tiny energy packets. Each packet, which is like a “particle” of energy, is called a photon. Extending Planck's quantum theory, Einstein deduced that each photon must have an energy equal to Planck's constant times the frequency of the light:
![]() GO FIGURE
GO FIGURE
Why is it necessary to carry out this experiment in an evacuated chamber?
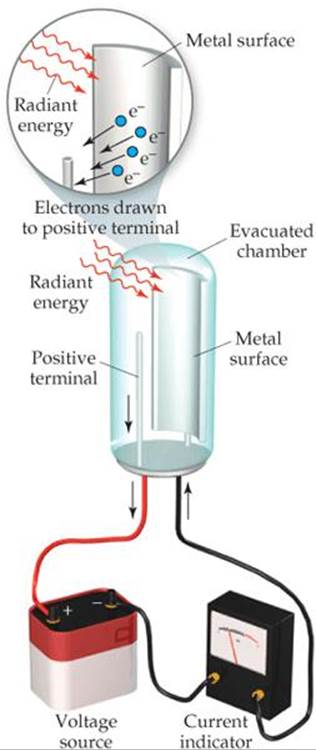
![]() FIGURE 6.7 The photoelectric effect.
FIGURE 6.7 The photoelectric effect.
![]()
Thus, radiant energy itself is quantized.
Under the right conditions, photons striking a metal surface can transfer their energy to electrons in the metal. A certain amount of energy—called the work function —is required for the electrons to overcome the attractive forces holding them in the metal. If the photons striking the metal have less energy than the work function, the electrons do not acquire sufficient energy to escape from the metal, even if the light beam is intense. If the photons have energy greater than the work function of the particular metal, however, electrons are emitted. The intensity (brightness) of the light is related to the number of photons striking the surface per unit time but not to the energy of each photon. Einstein won the Nobel Prize in Physics in 1921 for his explanation of the photoelectric effect.
To better understand what a photon is, imagine you have a light source that produces radiation of a single wavelength. Further suppose that you could switch the light on and off faster and faster to provide ever-smaller bursts of energy. Einstein's photon theory tells us that you would eventually come to the smallest energy burst, given by E = hv. This smallest burst consists of a single photon of light.
SAMPLE EXERCISE 6.3 Energy of a Photon
Calculate the energy of one photon of yellow light that has a wavelength of 589 nm.
SOLUTION
Analyze Our task is to calculate the energy, E, of a photon, given λ = 589 nm.
Plan We can use Equation 6.1 to convert the wavelength to frequency:
v = c/λ
We can then use Equation 6.3 to calculate energy:
E = hv
Solve The frequency, v, is calculated from the given wavelength, as shown in Sample Exercise 6.2:
v = c/λ = 5.99 × 1014 s–1
The value of Planck's constant, h, is given both in the text and in the table of physical constants on the inside back cover of the text, and so we can easily calculate E:
E = (6.626 × 10–34 J-s)(5.09 × 1014 s−1) = 3.37 × 10–19 J
Comment If one photon of radiant energy supplies 3.37 × 10–19 J, then one mole of these photons will supply
(6.02 × 1023 photons/mol)(3.37 × 10–19 J/photon) = 2.03 × 105J/mol
PRACTICE EXERCISE
(a) A laser emits light that has a frequency of 4.69 × 1014 s–1. What is the energy of one photon of this radiation? (b) If the laser emits a pulse containing 5.0 × 1017 photons of this radiation, what is the total energy of that pulse? (c) If the laser emits 1.3 × 10–2 J of energy during a pulse, how many photons are emitted?
Answers: (a) 3.11 × 10–19 J, (b) 0.16 J, (c) 4.2 × 1016 photons
The idea that the energy of light depends on its frequency helps us understand the diverse effects of different kinds of electromagnetic radiation. For example, because of the high frequency (short wavelength) of X-rays (Figure 6.4), X-ray photons cause tissue damage and even cancer. Thus, signs are normally posted around X-ray equipment warning us of high-energy radiation.
Although Einstein's theory of light as a stream of photons rather than a wave explains the photoelectric effect and a great many other observations, it also poses a dilemma. Is light a wave, or is it particle-like? The only way to resolve this dilemma is to adopt what might seem to be a bizarre position: We must consider that light possesses both wave-like and particle-like characteristics and, depending on the situation, will behave more like waves or more like particles. We will soon see that this dual nature of light is also a characteristic trait of matter.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Which has more energy, a photon of infrared light or a photon of ultraviolet light?