CHEMISTRY THE CENTRAL SCIENCE
1 INTRODUCTION: MATTER AND MEASUREMENT
1.5 UNCERTAINTY IN MEASUREMENT
Two kinds of numbers are encountered in scientific work: exact numbers (those whose values are known exactly) and inexact numbers (those whose values have some uncertainty). Most of the exact numbers we will encounter in this book have defined values. For example, there are exactly 12 eggs in a dozen, exactly 1000 g in a kilogram, and exactly 2.54 cm in an inch. The number 1 in any conversion factor, such as 1 m = 100cm or 1kg = 2.20461b, is an exact number. Exact numbers can also result from counting objects. For example, we can count the exact number of marbles in a jar or the exact number of people in a classroom.
Numbers obtained by measurement are always inexact. The equipment used to measure quantities always has inherent limitations (equipment errors), and there are differences in how different people make the same measurement (human errors). Suppose ten students with ten balances are to determine the mass of the same dime. The ten measurements will probably vary slightly for various reasons. The balances might be calibrated slightly differently, and there might be differences in how each student reads the mass from the balance. Remember: Uncertainties always exist in measured quantities.
GIVE IT SOME THOUGHT
Which of the following is an inexact quantity:
a. the number of people in your chemistry class,
b. the mass of a penny,
c. the number of grams in a kilogram?
Precision and Accuracy
The terms precision and accuracy are often used in discussing the uncertainties of measured values. Precision is a measure of how closely individual measurements agree with one another. Accuracy refers to how closely individual measurements agree with the correct, or “true,” value. The dart analogy in 
FIGURE 1.23 illustrates the difference between these two concepts.
GO FIGURE
How would the darts be positioned on the target for the case of “good accuracy, poor precision”?
FIGURE 1.23 Precision and accuracy.
In the laboratory we often perform several “trials” of an experiment and average the results. The precision of the measurements is often expressed in terms of the standard deviation (Appendix A.5), which reflects how much the individual measurements differ from the average. We gain confidence in our measurements if we obtain nearly the same value each time—that is, the standard deviation is small. Figure 1.23 reminds us, however, that precise measurements can be inaccurate. For example, if a very sensitive balance is poorly calibrated, the masses we measure will be consistently either high or low. They will be inaccurate even if they are precise.
Significant Figures
Suppose you determine the mass of a dime on a balance capable of measuring to the nearest 0.0001 g. You could report the mass as 2.2405 ± 0.0001 g. The ± notation (read “plus or minus”) expresses the magnitude of the uncertainty of your measurement. In much scientific work we drop the ± notation with the understanding that there is always some uncertainty in the last digit reported for any measured quantity.
FIGURE 1.24 shows a thermometer with its liquid column between two scale marks. We can read the certain digits from the scale and estimate the uncertain one. Seeing that the liquid is between the 25 °C and 30 °C marks, we estimate the temperature to be 27 °C, being uncertain of the second digit of our measurement.
All digits of a measured quantity, including the uncertain one, are called significant figures. A measured mass reported as 2.2 g has two significant figures, whereas one reported as 2.2405 g has five significant figures. The greater the number of significant figures, the greater the certainty implied for the measurement.
SAMPLE EXERCISE 1.5 Relating Significant Figures to the Uncertainty of a Measurement
What difference exists between the measured values 4.0 g and 4.00 g?
SOLUTION
The value 4.0 has two significant figures, whereas 4.00 has three. This difference implies that the 4.0 has more uncertainty. A mass reported as 4.0 g indicates that the uncertainty is in the first decimal place. Thus, the mass might be anything between 3.9 and 4.1 g, which we can represent as 4.0 ± 0.1g. A mass reported as 4.00 g indicates that the uncertainty is in the second decimal place. Thus, the mass might be anything between 3.99 and 4.01 g, which we can represent as 4.00 ± 0.01g. (Without further information, we cannot be sure whether the difference in uncertainties of the two measurements reflects the precision or the accuracy of the measurement.)
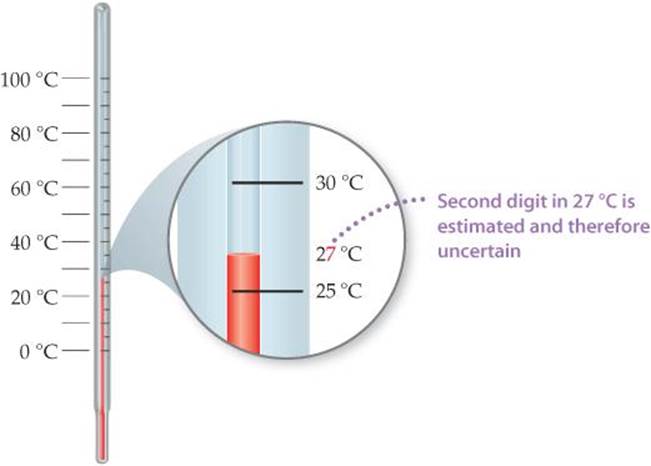
FIGURE 1.24 Uncertainty and significant figures in a measurement.
PRACTICE EXERCISE
A sample that has a mass of about 25 g is placed on a balance that has a precision of ± 0.001g. How many significant figures should be reported for this measurement?
Answer: five, as in the measurement 24.995 g, the uncertainty being in the third decimal place
To determine the number of significant figures in a reported measurement, read the number from left to right, counting the digits starting with the first digit that is not zero. In any measurement that is properly reported, all nonzero digits are significant. Because zeros can be used either as part of the measured value or merely to locate the decimal point, they may or may not be significant:
1. Zeros between nonzero digits are always significant—1005 kg (four significant figures); 7.03 cm (three significant figures).
2. Zeros at the beginning of a number are never significant; they merely indicate the position of the decimal point—0.02 g (one significant figure); 0.0026 cm (two significant figures).
3. Zeros at the end of a number are significant if the number contains a decimal point—0.0200 g (three significant figures); 3.0 cm (two significant figures).
A problem arises when a number ends with zeros but contains no decimal point. In such cases, it is normally assumed that the zeros are not significant. Exponential notation (Appendix A.1) can be used to indicate whether end zeros are significant. For example, a mass of 10,300 g can be written to show three, four, or five significant figures depending on how the measurement is obtained:
In these numbers all the zeros to the right of the decimal point are significant (rules 1 and 3). (The exponential term 104 does not add to the number of significant figures.)
SAMPLE EXERCISE 1.6 Determining the Number of Significant Figures in a Measurement
How many significant figures are in each of the following numbers (assume that each number is a measured quantity): (a) 4.003, (b) 6.023 × 1023, (c) 5000?
SOLUTION
(a) Four; the zeros are significant figures. (b) Four; the exponential term does not add to the number of significant figures. (c) One; we assume that the zeros are not significant when there is no decimal point shown. If the number has more significant figures, a decimal point should be employed or the number written in exponential notation. Thus, 5000. has four significant figures, whereas 5.00 × 103 has three.
PRACTICE EXERCISE
How many significant figures are in each of the following measurements: (a) 3.549 g, (b) 2.3 × 104cm, (c) 0.00134 m3?
Answers: (a) four, (b) two, (c) three
Significant Figures in Calculations
When carrying measured quantities through calculations, the least certain measurement limits the certainty of the calculated quantity and thereby determines the number of significant figures in the final answer. The final answer should be reported with only one uncertain digit. To keep track of significant figures in calculations, we will make frequent use of two rules, one for addition and subtraction, and another for multiplication and division.
1. For addition and subtraction, the result has the same number of decimal places as the measurement with the fewest decimal places. When the result contains more than the correct number of significant figures, it must be rounded off. Consider the following example in which the uncertain digits appear in color:
We report the result as 104.8 because 83.1 has only one decimal place.
2. For multiplication and division, the result contains the same number of significant figures as the measurement with the fewest significant figures. When the result contains more than the correct number of significant figures, it must be rounded off. For example, the area of a rectangle whose measured edge lengths are 6.221 cm and 5.2 cm should be reported as 32 cm2 even though a calculator shows the product to have more digits:
because 5.2 has two significant figures.
Notice that for addition and subtraction, decimal places are counted in determining how many digits to report in an answer, whereas for multiplication and division, significant figures are counted in determining how many digits to report.
In determining the final answer for a calculated quantity, exact numbers are assumed to have an infinite number of significant figures. Thus, when we say, “There are 12 inches in 1 foot,” the number 12 is exact, and we need not worry about the number of significant figures in it.
In rounding off numbers, look at the leftmost digit to be removed:
• If the leftmost digit removed is less than 5, the preceding number is left unchanged. Thus, rounding 7.248 to two significant figures gives 7.2.
• If the leftmost digit removed is 5 or greater, the preceding number is increased by 1. Rounding 4.735 to three significant figures gives 4.74, and rounding 2.376 to two significant figures gives 2.4.*
SAMPLE EXERCISE 1.7 Determining the Number of Significant Figures in a Calculated Quantity
The width, length, and height of a small box are 15.5 cm, 27.3 cm, and 5.4 cm, respectively. Calculate the volume of the box, using the correct number of significant figures in your answer.
SOLUTION
In reporting the volume, we can show only as many significant figures as given in the dimension with the fewest significant figures, that for the height (two significant figures):
A calculator used for this calculation shows 2285.01, which we must round off to two significant figures. Because the resulting number is 2300, it is best reported in exponential notation, 2.3 × 103, to clearly indicate two significant figures.
PRACTICE EXERCISE
It takes 10.5 s for a sprinter to run 100.00 m. Calculate her average speed in meters per second, and express the result to the correct number of significant figures.
Answer: 9.52m/s (three significant figures)
SAMPLE EXERCISE 1.8 Determining the Number of Significant Figures in a Calculated Quantity
A gas at 25 °C fills a container whose volume is 1.05 × 103 cm3. The container plus gas has a mass of 837.6 g. The container, when emptied of all gas, has a mass of 836.2 g. What is the density of the gas at 25 °C?
SOLUTION
To calculate the density, we must know both the mass and the volume of the gas. The mass of the gas is just the difference in the masses of the full and empty container:
(837.6 – 836.2) g = 1.4 g
In subtracting numbers, we determine the number of significant figures in our result by counting decimal places in each quantity. In this case each quantity has one decimal place. Thus, the mass of the gas, 1.4 g, has one decimal place.
Using the volume given in the question, 1.05 × 103 cm3, and the definition of density, we have
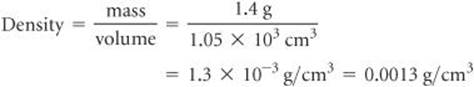
In dividing numbers, we determine the number of significant figures in our result by counting the number of significant figures in each quantity. There are two significant figures in our answer, corresponding to the smaller number of significant figures in the two numbers that form the ratio. Notice that in this example, following the rules for determining significant figures gives an answer containing only two significant figures, even though each of the measured quantities contained at least three significant figures.
PRACTICE EXERCISE
To how many significant figures should the mass of the container be measured (with and without the gas) in Sample Exercise 1.8 for the density to be calculated to three significant figures?
Answer: five (For the difference in the two masses to have three significant figures, there must be two decimal places in the masses of the filled and empty containers. Therefore, each mass must be measured to five significant figures.)
When a calculation involves two or more steps and you write answers for intermediate steps, retain at least one nonsignificant digit for the intermediate answers. This procedure ensures that small errors from rounding at each step do not combine to affect the final result. When using a calculator, you may enter the numbers one after another, rounding only the final answer. Accumulated rounding-off errors may account for small differences among results you obtain and answers given in the text for numerical problems.