CHEMISTRY THE CENTRAL SCIENCE

6 ELECTRONIC STRUCTURE OF ATOMS

6.4 THE WAVE BEHAVIOR OF MATTER

In the years following the development of Bohr's model for the hydrogen atom, the dual nature of radiant energy became a familiar concept. Depending on the experimental circumstances, radiation appears to have either a wave-like or a particle-like (photon) character. Louis de Broglie (1892–1987), who was working on his Ph.D. thesis in physics at the Sorbonne in Paris, boldly extended this idea. If radiant energy could, under appropriate conditions, behave as though it were a stream of particles (photons), could matter, under appropriate conditions, possibly show the properties of a wave?

De Broglie suggested that an electron moving about the nucleus of an atom behaves like a wave and therefore has a wavelength. He proposed that the wavelength of the electron, or of any other particle, depends on its mass, m, and on its velocity, v:

(where h is Planck's constant). The quantity mv for any object is called its momentum. De Broglie used the term matter waves to describe the wave characteristics of material particles.

Because de Broglie's hypothesis is applicable to all matter, any object of mass m and velocity v would give rise to a characteristic matter wave. However, Equation 6.8 indicates that the wavelength associated with an object of ordinary size, such as a golf ball, is so tiny as to be completely unobservable. This is not so for an electron because its mass is so small, as we see in Sample Exercise 6.5.

SAMPLE EXERCISE 6.5 Matter Waves

What is the wavelength of an electron moving with a speed of 5.97 × 106 m/s? The mass of the electron is 9.11 × 10^–31 kg.

SOLUTION

Analyze We are given the mass, m, and velocity, v, of the electron, and we must calculate its de Broglie wavelength, λ.

Plan The wavelength of a moving particle is given by Equation 6.8, so λ is calculated by inserting the known quantities h, m, and v. In doing so, however, we must pay attention to units.

Solve Using the value of Planck's constant,

h = 6.626 × 10^–34 J-s

we have the following:

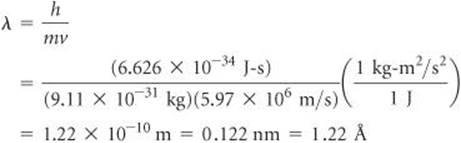
Comment By comparing this value with the wavelengths of electromagnetic radiation shown in Figure 6.4, we see that the wavelength of this electron is about the same as that of X-rays.

PRACTICE EXERCISE

Calculate the velocity of a neutron whose de Broglie wavelength is 500 pm. The mass of a neutron is given in the table inside the back cover of the text.

Answer: 7.92 × 10² m/s

A few years after de Broglie published his theory, the wave properties of the electron were demonstrated experimentally. When X-rays pass through a crystal, an interference pattern results that is characteristic of the wavelike properties of electromagnetic radiation. This phenomenon is called X-ray diffraction. As electrons pass through a crystal, they are similarly diffracted. Thus, a stream of moving electrons exhibits the same kinds of wave behavior as X-rays and all other types of electromagnetic radiation.

The technique of electron diffraction has been highly developed. In the electron microscope, for instance, the wave characteristics of electrons are used to obtain images at the atomic scale. This microscope is an important tool for studying surface phenomena at very high magnifications (FIGURE 6.13). Electron microscopes can magnify objects by 3,000,000 times (×), far more than can be done with visible light (1000×), because the wavelength of the electrons is so much smaller than the wavelengths of visible light.

GIVE IT SOME THOUGHT

A baseball pitcher throws a fastball that moves at 95 miles per hour. Does that moving baseball generate matter waves? If so, can we observe them?

The Uncertainty Principle

The discovery of the wave properties of matter raised some new and interesting questions. Consider, for example, a ball rolling down a ramp. Using the equations of classical physics, we can calculate, with great accuracy, the ball's position, direction of motion, and speed at any instant. Can we do the same for an electron, which exhibits wave properties? A wave extends in space and its location is not precisely defined. We might therefore anticipate that it is impossible to determine exactly where an electron is located at a specific instant.

The German physicist Werner Heisenberg (FIGURE 6.14) proposed that the dual nature of matter places a fundamental limitation on how precisely we can know both the location and the momentum of an object at a given instant. The limitation becomes important only when we deal with matter at the subatomic level (that is, with masses as small as that of an electron). Heisenberg's principle is called the uncertainty principle. When applied to the electrons in an atom, this principle states that it is impossible for us to know simultaneously both the exact momentum of the electron and its exact location in space.

FIGURE 6.13 Electrons as waves. The white dots in this transmission electron micrograph indicate the tops of columns of atoms.

FIGURE 6.14 Werner Heisenberg (1901-1976). During his postdoctoral assistantship with Niels Bohr, Heisenberg formulated his famous uncertainty principle. At 32 he was one of the youngest scientists to receive a Nobel Prize.

Heisenberg mathematically related the uncertainty in position, Δx, and the uncertainty in momentum, Δ(mv), to a quantity involving Planck's constant:

A brief calculation illustrates the dramatic implications of the uncertainty principle. The electron has a mass of 9.11 × 10^–31 kg and moves at an average speed of about 5 × 10⁶ m/s in a hydrogen atom. Let's assume that we know the speed to an uncertainty of 1% [that is, an uncertainty of (0.01)(5 × 10⁶ m/s) = 5 × 10⁴ m/s] and that this is the only important source of uncertainty in the momentum, so that Δ(mv) = m Δv. We can use Equation 6.9 to calculate the uncertainty in the position of the electron:

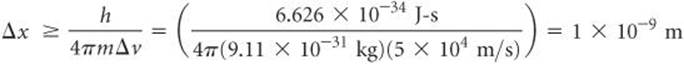
Because the diameter of a hydrogen atom is about 1 × 10^–10 m, the uncertainty in the position of the electron in the atom is an order of magnitude greater than the size of the atom. Thus, we have essentially no idea where the electron is located in the atom. On the other hand, if we were to repeat the calculation with an object of ordinary mass, such as a tennis ball, the uncertainty would be so small that it would be inconsequential. In that case, m is large and Δx is out of the realm of measurement and therefore of no practical consequence.

De Broglie's hypothesis and Heisenberg's uncertainty principle set the stage for a new and more broadly applicable theory of atomic structure. In this approach, any attempt to define precisely the instantaneous location and momentum of the electron is abandoned. The wave nature of the electron is recognized, and its behavior is described in terms appropriate to waves. The result is a model that precisely describes the energy of the electron while describing its location not precisely but rather in terms of probabilities.

A CLOSER LOOK
MEASUREMENT AND THE UNCERTAINTY PRINCIPLE

Whenever any measurement is made, some uncertainty exists. Our experience with objects of ordinary dimensions, such as balls or trains or laboratory equipment, indicates that using more precise instruments can decrease the uncertainty of a measurement. In fact, we might expect that the uncertainty in a measurement can be made indefinitely small. However, the uncertainty principle states that there is an actual limit to the accuracy of measurements. This limit is not a restriction on how well instruments can be made; rather, it is inherent in nature. This limit has no practical consequences when dealing with ordinary-sized objects, but its implications are enormous when dealing with subatomic particles, such as electrons.

To measure an object, we must disturb it, at least a little, with our measuring device. Imagine using a flashlight to locate a large rubber ball in a dark room. You see the ball when the light from the flashlight bounces off the ball and strikes your eyes. When a beam of photons strikes an object of this size, it does not alter its position or momentum to any practical extent. Imagine, however, that you wish to locate an electron by similarly bouncing light off it into some de-tector. Objects can be located to an accuracy no greater than the wavelength of the radiation used. Thus, if we want an accurate position measurement for an electron, we must use a short wavelength. This means that photons of high energy must be employed. The more energy the photons have, the more momentum they impart to the electron when they strike it, which changes the electron's motion in an unpredictable way. The attempt to measure accurately the electron's position introduces considerable uncertainty in its momentum; the act of measuring the electron's position at one moment makes our knowledge of its future position inaccurate.

Suppose, then, that we use photons of longer wavelength. Because these photons have lower energy, the momentum of the electron is not so appreciably changed during measurement, but its position will be correspondingly less accurately known. This is the essence of the uncertainty principle: There is an uncertainty in simultaneously knowing either the position or the momentum of the electron that cannot be reduced beyond a certain minimum level. The more accurately one is known, the less accurately the other is known. Although we can never know the exact position and momentum of the electron, we can talk about the probability of its being at certain locations in space. In Section 6.5 we introduce a model of the atom that provides the probability of finding electrons of specific energies at certain positions in atoms.

RELATED EXERCISES: 6.47 and 6.48

GIVE IT SOME THOUGHT

What is the principal reason we must consider the uncertainty principle when discussing electrons and other subatomic particles but not when discussing our macroscopic world?