CHEMISTRY THE CENTRAL SCIENCE
6 ELECTRONIC STRUCTURE OF ATOMS
6.5 QUANTUM MECHANICS AND ATOMIC ORBITALS
In 1926 the Austrian physicist Erwin Schrödinger (1887-1961) proposed an equation, now known as Schrödinger's wave equation, that incorporates both the wave-like behavior of the electron and its particle-like behavior. His work opened a new approach to dealing with subatomic particles, an approach known as quantum mechanics or wave mechanics. The application of Schrödinger's equation requires advanced calculus, and so we will not be concerned with its details. We will, however, qualitatively consider the results Schrödinger obtained because they give us a powerful new way to view electronic structure. Let's begin by examining the electronic structure of the simplest atom, hydrogen.
Schrödinger treated the electron in a hydrogen atom like the wave on a plucked guitar string (
FIGURE 6.15). Because such waves do not travel in space, they are called standing waves. Just as the plucked guitar string produces a standing wave that has a fundamental frequency and higher overtones (harmonics), the electron exhibits a lowest-energy standing wave and higher-energy ones. Furthermore, just as the overtones of the guitar string have nodes, points where the amplitude of the wave is zero, so do the waves characteristic of the electron.
Solving Schrödinger's equation for the hydrogen atom leads to a series of mathematical functions called wave functions that describe the electron in an atom. These wave functions are usually represented by the symbol ψ (lowercase Greek letter psi). Although the wave function has no direct physical meaning, the square of the wave function, ψ2, provides information about the electron's location when it is in an allowed energy state.
For the hydrogen atom, the allowed energies are the same as those predicted by the Bohr model. However, the Bohr model assumes that the electron is in a circular orbit of some particular radius about the nucleus. In the quantum mechanical model, the electron's location cannot be described so simply.
According to the uncertainty principle, if we know the momentum of the electron with high accuracy, our simultaneous knowledge of its location is very uncertain. Thus, we cannot hope to specify the exact location of an individual electron around the nucleus. Rather, we must be content with a kind of statistical knowledge. We therefore speak of the probability that the electron will be in a certain region of space at a given instant. As it turns out, the square of the wave function, ψ2, at a given point in space represents the probability that the electron will be found at that location. For this reason, ψ2 is called either the probability density or the electron density.
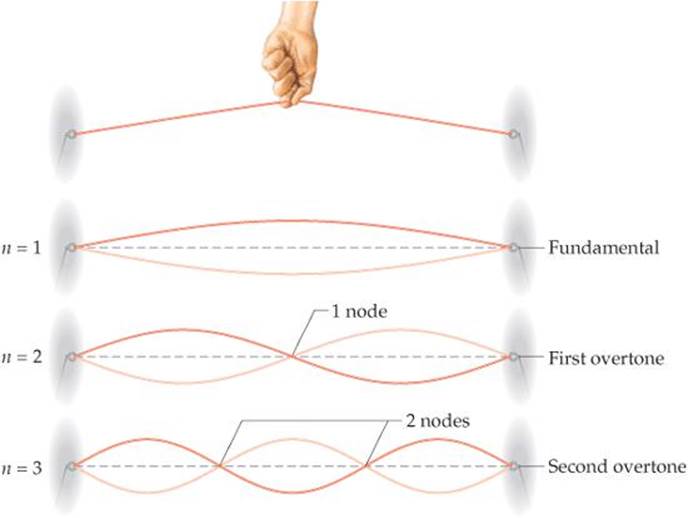
FIGURE 6.15 Standing waves in a vibrating string.
One way of representing the probability of finding the electron in various regions of an atom is shown in FIGURE 6.16, where the density of the dots represents the probability of finding the electron. The regions with a high density of dots correspond to relatively large values for ψ2and are therefore regions where there is a high probability of finding the electron. Based on this representation, we often describe atoms as consisting of a nucleus surrounded by an electron cloud.
GO FIGURE
Where in the figure is the region of highest electron density?
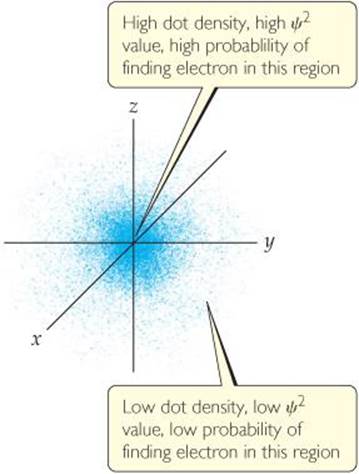
FIGURE 6.16 Electron-density distribution. This rendering represents the probability, ψ2, of finding the electron in a hydrogen atom in its ground state. The origin of the coordinate system is at the nucleus.
Orbitals and Quantum Numbers
The solution to Schrödinger's equation for the hydrogen atom yields a set of wave functions called orbitals. Each orbital has a characteristic shape and energy. For example, the lowest-energy orbital in the hydrogen atom has the spherical shape illustrated in Figure 6.16 and an energy of −2.18 × 10–18 J. Note that an orbital (quantum mechanical model, which describes electrons in terms of probabilities, visualized as “electron clouds”) is not the same as an orbit (Bohr model, which visualizes the electron moving in a physical orbit, like a planet around a star). The quantum mechanical model does not refer to orbits because the motion of the electron in an atom cannot be precisely determined (Heisenberg uncertainty principle).
The Bohr model introduced a single quantum number, n, to describe an orbit. The quantum mechanical model uses three quantum numbers, n, l, and ml, which result naturally from the mathematics used, to describe an orbital.
1. The principal quantum number, n, can have positive integral values 1, 2, 3, …. As n increases, the orbital becomes larger, and the electron spends more time farther from the nucleus. An increase in n also means that the electron has a higher energy and is therefore less tightly bound to the nucleus. For the hydrogen atom, En = –(2.18 × 10–18 J)(1/n2), as in the Bohr model.
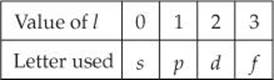
2. The second quantum number—the angular momentum quantum number, l—can have integral values from 0 to (n – 1) for each value of n. This quantum number defines the shape of the orbital. The value of l for a particular orbital is generally designated by the letters s, p, d, and f, *corresponding to l values of 0, 1, 2, and 3:
3. The magnetic quantum number, ml, can have integral values between –l and l, including zero. This quantum number describes the orientation of the orbital in space, as we discuss in Section 6.6.
Notice that because the value of n can be any positive integer, an infinite number of orbitals for the hydrogen atom are possible. At any given instant, however, the electron in a hydrogen atom is described by only one of these orbitals—we say that the electron occupies a certain orbital. The remaining orbitals are unoccupied for that particular state of the hydrogen atom.
GIVE IT SOME THOUGHT
What is the difference between an orbit in the Bohr model of the hydrogen atom and an orbital in the quantum mechanical model?
The collection of orbitals with the same value of n is called an electron shell. All the orbitals that have n = 3, for example, are said to be in the third shell. The set of orbitals that have the same n and l values is called a subshell. Each subshell is designated by a number (the value of n)and a letter (s, p, d, or f, corresponding to the value of l). For example, the orbitals that have n = 3 and l = 2 are called 3d orbitals and are in the 3d subshell.
TABLE 6.2 • Relationship among Values of n, l, and ml through n = 4
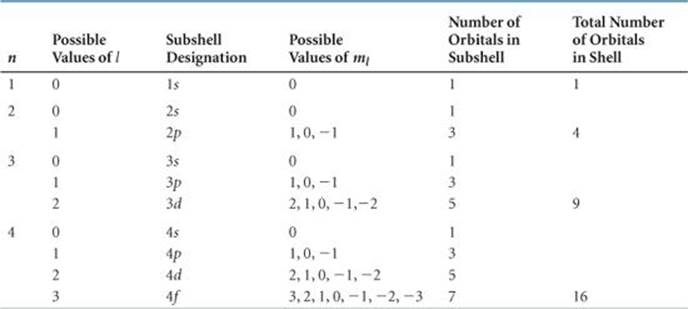
TABLE 6.2 summarizes the possible values of l and ml for values of n through n = 4. The restrictions on possible values give rise to the following very important observations:
1. The shell with principal quantum number n consists of exactly n subshells. Each subshell corresponds to a different allowed value of l from 0 to (n — 1). Thus, the first shell (n = 1) consists of only one subshell, the 1s (l = 0); the second shell (n = 2) consists of two subshells, the 2s (l= 0) and 2p (l = 1); the third shell consists of three subshells, 3s, 3p, and 3d, and so forth.
2. Each subshell consists of a specific number of orbitals. Each orbital corresponds to a different allowed value of ml. For a given value of l, there are (2l + 1) allowed values of ml, ranging from –l to +l. Thus, each s (l = 0) subshell consists of one orbital; each p (l = 1) sub-shell consists of three orbitals; each d (l = 2) subshell consists of five orbitals, and so forth.
3. The total number of orbitals in a shell is n2, where n is the principal quantum number of the shell. The resulting number of orbitals for the shells—1, 4, 9, 16—are related to a pattern seen in the periodic table: We see that the number of elements in the rows of the periodic table—2, 8, 18, and 32—equals twice these numbers. We will discuss this relationship further in Section 6.9.
FIGURE 6.17 shows the relative energies of the hydrogen atom orbitals through n = 3. Each box represents an orbital, and orbitals of the same subshell, such as the three 2p orbitals, are grouped together. When the electron occupies the lowest-energy orbital (1s), the hydrogen atom is said to be in its ground state. When the electron occupies any other orbital, the atom is in an excited state. (The electron can be excited to a higher-energy orbital by absorption of a photon of appropriate energy.) At ordinary temperatures, essentially all hydrogen atoms are in the ground state.
GIVE IT SOME THOUGHT
Notice in Figure 6.17 that the energy difference between the n = 1 and n = 2 levels is much greater than the energy difference between the n = 2 and n = 3 levels. How does Equation 6.5 explain this trend?
GO FIGURE
If the fourth shell (the n = 4 energy level) were shown, how many sub-shells would it contain? How would they be labeled?
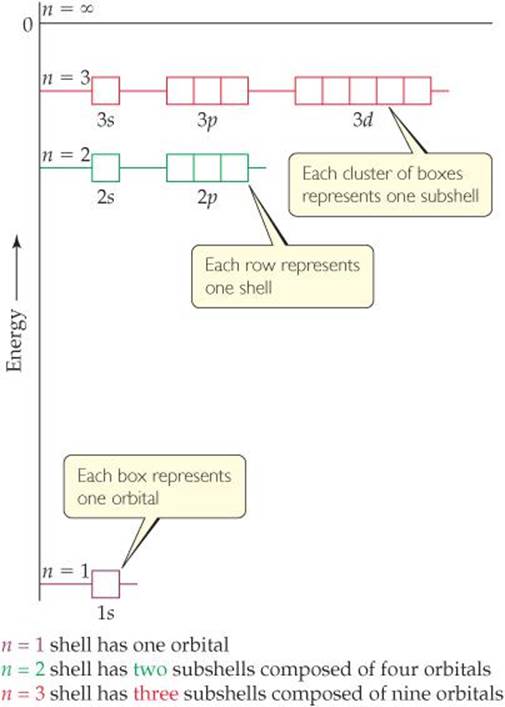
FIGURE 6.17 Energy levels in the hydrogen atom.
SAMPLE EXERCISE 6.6 Subshells of the Hydrogen Atom
(a) Without referring to Table 6.2, predict the number of subshells in the fourth shell, that is, for n = 4. (b) Give the label for each of these subshells. (c) How many orbitals are in each of these subshells?
Analyze and Plan We are given the value of the principal quantum number, n. We need to determine the allowed values of l and ml for this given value of n and then count the number of orbitals in each subshell.
SOLUTION
There are four subshells in the fourth shell, corresponding to the four possible values of l (0, 1, 2, and 3).
These subshells are labeled 4s, 4p, 4d, and 4f. The number given in the designation of a subshell is the principal quantum number, n; the letter designates the value of the angular momentum quantum number, l: for l = 0, s; for l = 1, p; for l = 2, d; for l = 3,f.
There is one 4s orbital (when l = 0, there is only one possible value of ml : 0). There are three 4p orbitals (when l = 1, there are three possible values of ml : 1, 0, – 1). There are five 4d orbitals (when l = 2, there are five allowed values of ml : 2, 1, 0, –1, –2). There are seven 4f orbitals (when l = 3, there are seven permitted values of ml : 3, 2, 1, 0, –1, –2, –3).
PRACTICE EXERCISE
(a) What is the designation for the subshell with n = 5 and l = 1? (b) How many orbitals are in this subshell? (c) Indicate the values of ml for each of these orbitals.
Answers: (a) 5p; (b) 3; (c) 1, 0, –1