CHEMISTRY THE CENTRAL SCIENCE
6 ELECTRONIC STRUCTURE OF ATOMS
6.7 MANY-ELECTRON ATOMS
One of our goals in this chapter has been to determine the electronic structures of atoms. So far, we have seen that quantum mechanics leads to an elegant description of the hydrogen atom. This atom, however, has only one electron. How does our description change when we consider an atom with two or more electrons (a many-electron atom)? To describe such an atom, we must consider the nature of orbitals and their relative energies as well as how the electrons populate the available orbitals.
GO FIGURE
Not all of the orbitals in the n = 4 shell are shown in this figure. Which subshells are missing?
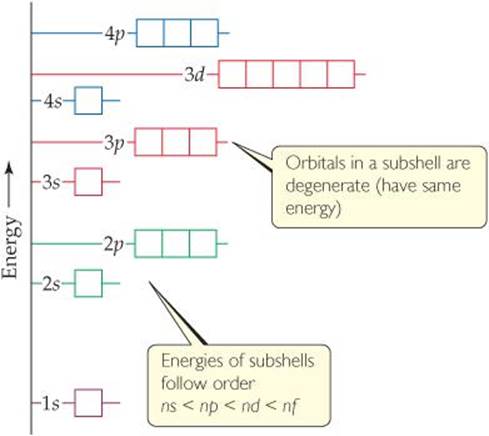
FIGURE 6.24 General energy ordering of orbitals for a many-electron atom.
Orbitals and Their Energies
We can describe the electronic structure of a many-electron atom in terms of orbitals like those of the hydrogen atom. Thus, we continue to designate orbitals as ls, 2px, and so forth. Further, these orbitals have the same general shapes as the corresponding hydrogen orbitals.
Although the shapes of the orbitals of a many-electron atom are the same as those for hydrogen, the presence of more than one electron greatly changes the energies of the orbitals. In hydrogen the energy of an orbital depends only on its principal quantum number, n (Figure 6.17). For instance, the 3s, 3p, and 3d subshells all have the same energy. In a many-electron atom, however, the electron-electron repulsions cause the various subshells in a given shell to be at different energies, as shown in 
FIGURE 6.24. To explain this fact, we must consider the forces between the electrons and how these forces are affected by the shapes of the orbitals. We will, however, forgo this analysis until Chapter 7.
The important idea is this: In a many-electron atom, for a given value of n, the energy of an orbital increases with increasing value of l. For example, notice in Figure 6.24 that the n = 3 orbitals increase in energy in the order 3s <3p <3d. Notice also that all orbitals of a given subshell (such as the five 3d orbitals) have the same energy as one another. Orbitals with the same energy are said to be degenerate.
Figure 6.24 is a qualitative energy-level diagram; the exact energies of the orbitals and their spacings differ from one atom to another.
GIVE IT SOME THOUGHT
a. How may orbitals have the principal quantum number n = 3?
b. In a many-electron atom, what are the relative energies of these orbitals?
Electron Spin and the Pauli Exclusion Principle
We have now seen that we can use hydrogen-like orbitals to describe many-electron atoms. What, however, determines which orbitals the electrons occupy? That is, how do the electrons of a many-electron atom populate the available orbitals? To answer this question, we must consider an additional property of the electron.
When scientists studied the line spectra of many-electron atoms in great detail, they noticed a very puzzling feature: Lines that were originally thought to be single were actually closely spaced pairs. This meant, in essence, that there were twice as many energy levels as there were “supposed” to be. In 1925 the Dutch physicists George Uhlenbeck and Samuel Goudsmit proposed a solution to this dilemma. They postulated that electrons have an intrinsic property, called electron spin, that causes each electron to behave as if it were a tiny sphere spinning on its own axis.
By now it probably does not surprise you to learn that electron spin is quantized. This observation led to the assignment of a new quantum number for the electron, in addition to n, l, and ml, which we have already discussed. This new quantum number, the spin magnetic quantum number, is denoted ms (the subscript s stands for spin). Two possible values are allowed for 
, which was first interpreted as indicating the two opposite directions in which the electron can spin. A spinning charge produces a magnetic field. The two opposite directions of spin therefore produce oppositely directed magnetic fields (
FIGURE 6.25).* These two opposite magnetic fields lead to the splitting of spectral lines into closely spaced pairs.
Electron spin is crucial for understanding the electronic structures of atoms. In 1925 the Austrian-born physicist Wolfgang Pauli (1900-1958) discovered the principle that governs the arrangements of electrons in many-electron atoms. The Pauli exclusion principle states that no two electrons in an atom can have the same set of four quantum numbers n, l, ml, and ms. For a given orbital, the values of n, l, and ml are fixed. Thus, if we want to put more than one electron in an orbital and satisfy the Pauli exclusion principle, our only choice is to assign different ms values to the electrons. Because there are only two such values, we conclude that an orbital can hold a maximum of two electrons and they must have opposite spins. This restriction allows us to index the electrons in an atom, giving their quantum numbers and thereby defining the region in space where each electron is most likely to be found. It also provides the key to understanding the structure of the periodic table of the elements.
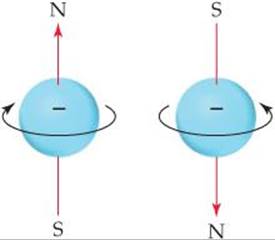
FIGURE 6.25 Electron spin. The electron behaves as if it were spinning about an axis, thereby generating a magnetic field whose direction depends on the direction of spin. The two directions for the magnetic field correspond to the two possible values for the spin quantum number,ms.
A CLOSER LOOK
EXPERIMENTAL EVIDENCE FOR ELECTRON SPIN
Even before electron spin had been proposed, there was experimental evidence that electrons had an additional property that needed explanation. In 1921, Otto Stern and Walter Gerlach succeeded in separating a beam of electrically neutral atoms into two groups by passing them through a nonhomogeneous magnetic field (FIGURE 6.26).
Let's assume they used a beam of hydrogen atoms (in actuality they used silver atoms, which contain just one unpaired electron). We would normally expect electrically neutral atoms to be unaffected by a magnetic field. However, the magnetic field arising from the electron's spin interacts with the magnet's field, deflecting the atom from its straight-line path. As shown in Figure 6.26, the magnetic field splits the beam in two, suggesting that there are two (and only two) equivalent values for the electron's magnetic field. The Stern-Gerlach experiment could be readily interpreted once it was realized that there are exactly two values for the spin of the electron. These values produce equal magnetic fields that are opposite in direction.
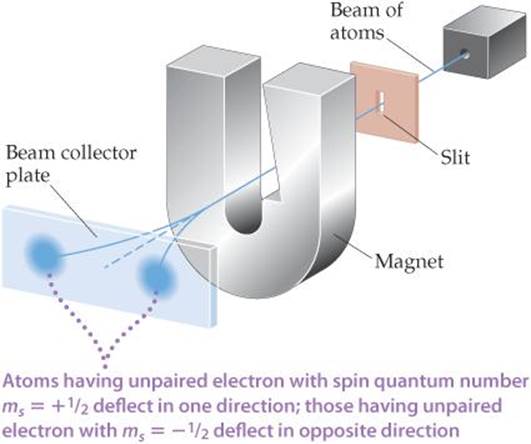
FIGURE 6.26 The Stern-Gerlach experiment.
CHEMISTRY AND LIFE
NUCLEAR SPIN AND MAGNETIC RESONANCE IMAGING
A major challenge facing medical diagnosis is seeing inside the human body. Until recently, this was accomplished primarily by using X-rays to image human bones, muscles, and organs. However, there are several drawbacks to using X-rays for medical imaging. First, X-rays do not give well-resolved images of overlapping physiological structures. Moreover, because damaged or diseased tissue often yields the same image as healthy tissue, X-rays frequently fail to detect illness or injuries. Finally, X-rays are high-energy radiation that can cause physiological harm, even in low doses.
During the 1980s, a technique called magnetic resonance imaging (MRI) moved to the forefront of medical imaging technology. The foundation of MRI is a phenomenon called nuclear magnetic resonance (NMR), which was discovered in the mid-1940s. Today NMR has become one of the most important spectroscopic methods used in chemistry. It is based on the observation that, like electrons, the nuclei of many elements possess an intrinsic spin. Like electron spin, nuclear spin is quantized. For example, the nucleus of H has two possible magnetic nuclear spin quantum numbers, 
and 
. The hydrogen nucleus is the most common one studied by NMR.
A spinning hydrogen nucleus acts like a tiny magnet. In the absence of external effects, the two spin states have the same energy. However, when the nuclei are placed in an external magnetic field, they can align either parallel or opposed (antiparallel) to the field, depending on their spin. The parallel alignment is lower in energy than the antiparallel one by a certain amount, AE (FIGURE 6.27). If the nuclei are irradiated with photons having energy equal to AE, the spin of the nuclei can be “flipped,” that is, excited from the parallel to the antiparallel alignment. Detection of the flipping of nuclei between the two spin states leads to an NMR spectrum. The radiation used in an NMR experiment is in the radiofrequency range, typically 100 to 900 MHz, which is far less energetic per photon than X-rays.
Because hydrogen is a major constituent of aqueous body fluids and fatty tissue, the hydrogen nucleus is the most convenient one for (study by MRI. In MRI a person's body is placed in a strong magnetic field. By irradiating the body with pulses of radiofrequency radiation and using sophisticated detection techniques, medical technicians can image tissue at specific depths in the body, giving pictures with spectacular detail (FIGURE 6.28). The ability to sample at different depths allows the technicians to construct a three-dimensional picture of the body.
MRI has none of the disadvantages of X-rays. Diseased tissue appears very different from healthy tissue, resolving overlapping structures at different depths in the body is much easier, and the radio frequency radiation is not harmful to humans in the doses used. The technique has had such a profound influence on the modern practice of medicine that Paul Lauterbur, a chemist, and Peter Mansfield, a physicist, were awarded the 2003 Nobel Prize in Physiology or Medicine for their discoveries concerning MRI. The major drawback of this technique is expense: The current cost of a new MRI instrument for clinical applications is over $1.5 million.
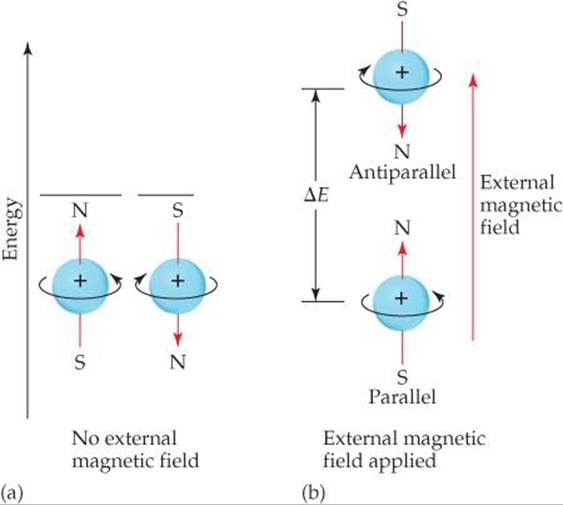
FIGURE 6.27 Nuclear spin. Like electron spin, nuclear spin generates a small magnetic field and has two allowed values. (a) In the absence of an external magnetic field, the two spin states have the same energy. (b) When an external magnetic field is applied, the spin state in which the spin direction is parallel to the direction of the external field is lower in energy than the spin state in which the spin direction is antiparallel to the field direction. The energy difference, ΔE, is in the radio frequency portion of the electromagnetic spectrum.
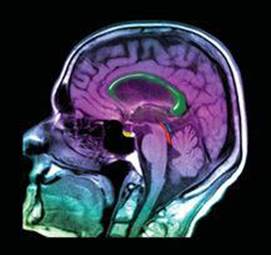
FIGURE 6.28 MRI image. This image of a human head, obtained using magnetic resonance imaging, shows a normal brain, airways, and facial tissues.
RELATED EXERCISE: 6.93