CHEMISTRY THE CENTRAL SCIENCE
7 PERIODIC PROPERTIES OF THE ELEMENTS
7.2 EFFECTIVE NUCLEAR CHARGE
Many properties of atoms depend on electron configuration and on how strongly the outer electrons in the atoms are attracted to the nucleus. Coulomb's law tells us that the strength of the interaction between two electrical charges depends on the magnitudes of the charges and on the distance between them. ![]() (Section 2.3) Thus, the attractive force between an electron and the nucleus depends on the magnitude of the nuclear charge and on the average distance between the nucleus and the electron. The force increases as the nuclear charge increases and decreases as the electron moves farther from the nucleus.
(Section 2.3) Thus, the attractive force between an electron and the nucleus depends on the magnitude of the nuclear charge and on the average distance between the nucleus and the electron. The force increases as the nuclear charge increases and decreases as the electron moves farther from the nucleus.
In a many-electron atom, each electron is simultaneously attracted to the nucleus and repelled by the other electrons. In general, there are so many electron–electron repulsions that we cannot analyze the situation exactly. We can, however, estimate the attractive force between any one electron and the nucleus by considering how the electron interacts with the average environment created by the nucleus and the other electrons in the atom. We treat each electron as though it were moving in the net electric field created by the nucleus and the electron density of the other electrons. We view this net electric field as if it results from a single positive charge located at the nucleus, called the effective nuclear charge, Zeff. The effective nuclear charge acting on an electron in an atom is smaller than the actual nuclear charge (Zeff < Z) because the effective nuclear charge includes the effect of the other electrons in the atom.
In any many-electron atom, the inner electrons partially screen outer electrons from the attraction of the nucleus, and the relationship between Zeff and the number of protons in the nucleus Z is
![]()
where S is a positive number called the screening constant. It represents the portion of the nuclear charge that is screened from a valence electron by the other electrons in the atom. Because core electrons are most effective at screening a valence electron from the nucleus, the value of S is usually close to the number of core electrons in an atom. (Electrons in the same valence shell do not screen one another very effectively, but they do affect the value of S slightly; see “A Closer Look: Effective Nuclear Charge.”)
Let's look at the Na atom to see what to expect for the magnitude of Zeff. Sodium has the electron configuration [Ne]3s1. The nuclear charge is Z = 11 +, and there are 10 core electrons (1s22s22p6). We therefore expect S to equal 10 and the 3s electron to experience an effective nuclear charge of Zeff = 11 - 10 = 1+ (![]() FIGURE 7.2). The situation is more complicated, however, because the 3s electron has a small probability of being closer to the nucleus, in the region occupied by the core electrons.
FIGURE 7.2). The situation is more complicated, however, because the 3s electron has a small probability of being closer to the nucleus, in the region occupied by the core electrons. ![]() (Section 6.6) Thus, there is a probability that this electron experiences a greater attraction than our simple S = 10 model suggests. This greater attraction turns out to increase the value of Zeff for the 3s electron in Na from our expected Zeff = 1+ to Zeff = 2.5+. In other words, the fact that the 3s electron spends some small amount of time close to the nucleus changes the value of S in Equation 7.1 from 10 to 8.5.
(Section 6.6) Thus, there is a probability that this electron experiences a greater attraction than our simple S = 10 model suggests. This greater attraction turns out to increase the value of Zeff for the 3s electron in Na from our expected Zeff = 1+ to Zeff = 2.5+. In other words, the fact that the 3s electron spends some small amount of time close to the nucleus changes the value of S in Equation 7.1 from 10 to 8.5.
The notion of effective nuclear charge also explains an important effect we noted in Section 6.7: For a many-electron atom, the energies of orbitals with the same n value increase with increasing l value. For example, in the carbon atom, electron configuration 1s22s22p2, the energy of the 2p orbital (l = 1) is higher than that of the 2s orbital (l = 0) even though both orbitals are in the n = 2 shell (Figure 6.24). This difference in energies is due to the radial probability functions for the orbitals (![]() FIGURE 7.3). The greater attraction between the 2s electron and the nucleus leads to a lower energy for the 2s orbital than for the 2p orbital. The same reasoning explains the general trend in orbital energies (ns < np < nd) in many-electron atoms.
FIGURE 7.3). The greater attraction between the 2s electron and the nucleus leads to a lower energy for the 2s orbital than for the 2p orbital. The same reasoning explains the general trend in orbital energies (ns < np < nd) in many-electron atoms.
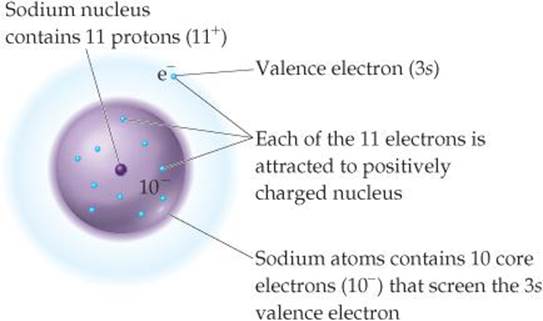
![]() FIGURE 7.2 Effective nuclear charge. The effective nuclear charge experienced by the valence electron in a sodium atom depends mostly on the 11 + charge of the nucleus and the 10- charge of the core electrons.
FIGURE 7.2 Effective nuclear charge. The effective nuclear charge experienced by the valence electron in a sodium atom depends mostly on the 11 + charge of the nucleus and the 10- charge of the core electrons.
![]() GO FIGURE
GO FIGURE
Which orbital has more electron density near the nucleus, 2s or 2p?
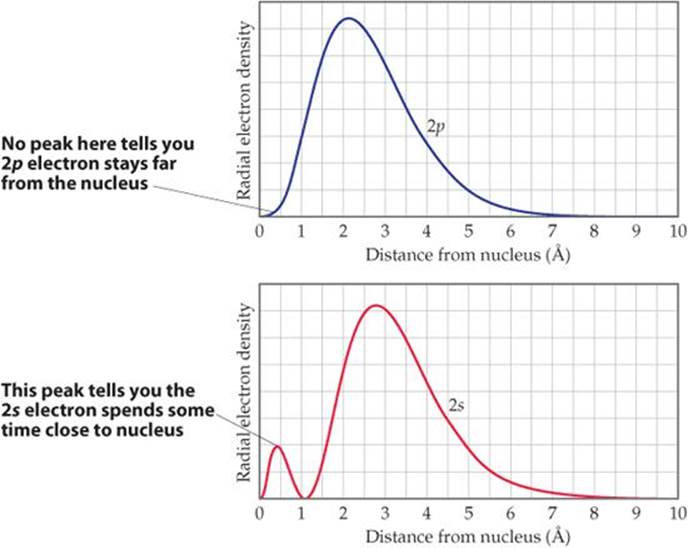
![]() FIGURE 7.3 2s and 2p radial probability functions.
FIGURE 7.3 2s and 2p radial probability functions.
Finally, let's examine trends in valence-electron Zeff values. The effective nuclear charge increases from left to right across any period of the periodic table. Although the number of core electrons stays the same across the period, the number of protons increases. The valence electrons added to counterbalance the increasing nuclear charge screen one another ineffectively. Thus, Zeff increases steadily. For example, the core electrons of lithium (1s22s1) screen the 2s valence electron from the 3+ nucleus fairly efficiently. Consequently, the valence electron experiences an effective nuclear charge of roughly 3 − 2 = 1+. For beryllium (1s22s2) the effective nuclear charge experienced by each valence electron is larger because here the 1s electrons screen a 4+ nucleus, and each 2s electron only partially screens the other. Consequently, the effective nuclear charge experienced by each 2s electron is about 4 − 2 = 2+.
 A CLOSER LOOK
A CLOSER LOOK
EFFECTIVE NUCLEAR CHARGE
To get a sense of how effective nuclear charge varies as both nuclear charge and number of electrons increase, consider ![]() FIGURE 7.4. Although the details of how the Zeff values in the graph were calculated are beyond the scope of our discussion, the trends are instructive.
FIGURE 7.4. Although the details of how the Zeff values in the graph were calculated are beyond the scope of our discussion, the trends are instructive.
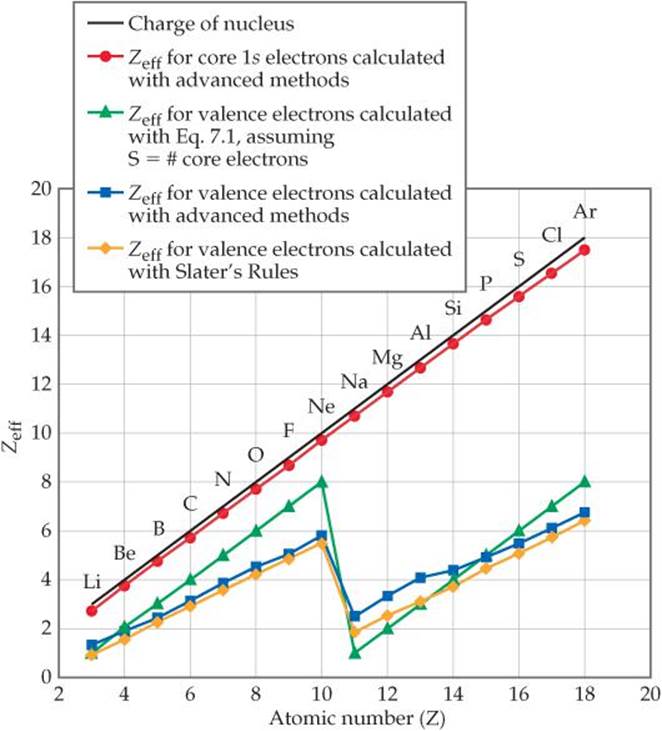
![]() FIGURE 7.4 Variations in effective nuclear charge for period 2 and period 3 elements. Moving from one element to the next in the periodic table, the increase in Zeff felt by the innermost (1s) electrons (red circles) closely tracks the increase in nuclear charge Z (black line) because these electrons are not screened. The results of several methods to calculate Zeff for valence electrons are shown in other colors.
FIGURE 7.4 Variations in effective nuclear charge for period 2 and period 3 elements. Moving from one element to the next in the periodic table, the increase in Zeff felt by the innermost (1s) electrons (red circles) closely tracks the increase in nuclear charge Z (black line) because these electrons are not screened. The results of several methods to calculate Zeff for valence electrons are shown in other colors.
The effective nuclear charge felt by the outermost electrons is smaller than that felt by inner electrons because of screening by the inner electrons. In addition, the effective nuclear charge felt by the outermost electrons does not increase as steeply with increasing atomic number because the valence electrons make a small but non-negligible contribution to the screening constant S. The most striking feature associated with the Zeff value for the outermost electrons is the sharp drop between the last period 2 element (Ne) and the first period 3 element (Na). This drop reflects the fact that the core electrons are much more effective than the valence electrons at screening the nuclear charge.
Because Zeff can be used to understand many physically measurable quantities, it is desirable to have a simple method for estimating it. The value of Z in Equation 7.1 is known exactly, so the challenge boils down to estimating the value of S. In the text, we estimated S by assuming that each core electron contributes 1.00 to S and the outer electrons contribute nothing. A more accurate approach was developed by John Slater, however, and we can use his approach if we limit ourselves to elements that do not have electrons in d or f subshells.
Electrons for which the principal quantum number n is larger than the value of n for the electron of interest contribute 0 to the value of S. Electrons with the same value of n as the electron of interest contribute 0.35 to the value of S. Electrons for which n is 1 less than n for the electron of interest contribute 0.85, while those with even smaller values of n contribute 1.00. For example, consider fluorine, which has the ground-state electron configuration 1s22s22p5. For a valence electron in fluorine, Slater's rules tell us that S = (0.35 × 6) + (0.85 × 2) = 3.8. (Slater's rules ignore the contribution of an electron to itself in screening; therefore, we consider only six n = 2 electrons, not all seven). Thus, Zeff = Z − S = 9 − 3.8 = 5.2+.
Values of Zeff estimated using the simple method outlined in the text, as well as those estimated with Slater's rules, are plotted in Figure 7.4. While neither of these methods exactly replicate the values of Zeff obtained from more sophisticated calculations, both methods effectively capture the periodic variation in Zeff. While Slater's approach is more accurate, the method outlined in the text does a reasonably good job of estimating Zeff despite its simplicity. For our purposes, therefore, we can assume that the screening constant S in Equation 7.1 is roughly equal to the number of core electrons.
RELATED EXERCISES: 7.11, 7.12, 7.13, 7.14, 7.34, 7.35, 7.84, 7.85
Going down a column, the effective nuclear charge experienced by valence electrons changes far less than it does across a period. For example, we would expect the effective nuclear charge experienced by the valence electrons in lithium and sodium to be about the same, roughly 3 − 2 = 1+ for lithium and 11 − 10 = 1+ for sodium. In fact, however, effective nuclear charge increases slightly as we go down a column because the more diffuse core electron cloud is less able to screen the valence electrons from the nuclear charge. In the case of the alkali metals, Zeff increases from 1.3+ for lithium, to 2.5+ for sodium, to 3.5+ for potassium.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Which would you expect to experience a greater effective nuclear charge, a 2p electron of a Ne atom or a 3s electron of a Na atom?