CHEMISTRY THE CENTRAL SCIENCE
1 INTRODUCTION: MATTER AND MEASUREMENT
1.6 DIMENSIONAL ANALYSIS
Throughout the text we use dimensional analysis in solving problems. In this approach, units are multiplied together, divided into each other, or “canceled.” Using dimensional analysis helps ensure that solutions to problems yield the proper units. Moreover, it provides a systematic way of solving many numerical problems and of checking solutions for possible errors.
The key to using dimensional analysis is the correct use of conversion factors to change one unit into another. A conversion factor is a fraction whose numerator and denominator are the same quantity expressed in different units. For example, 2.54 cm and 1 in. are the same length, 2.54cm = 1 in. This relationship allows us to write two conversion factors:
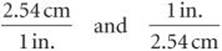
We use the first factor to convert inches to centimeters. For example, the length in centimeters of an object that is 8.50 in. long is
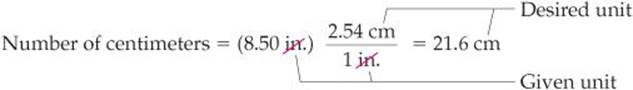
The unit inches in the denominator of the conversion factor cancels the unit inches in the given data (8.50 inches). The unit centimeters in the numerator of the conversion factor becomes the unit of the final answer. Because the numerator and denominator of a conversion factor are equal, multiplying any quantity by a conversion factor is equivalent to multiplying by the number 1 and so does not change the intrinsic value of the quantity. The length 8.50 in. is the same as the length 21.6 cm.
In general, we begin any conversion by examining the units of the given data and the units we desire. We then ask ourselves what conversion factors we have available to take us from the units of the given quantity to those of the desired one. When we multiply a quantity by a conversion factor, the units multiply and divide as follows:
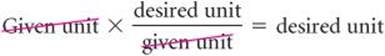
If the desired units are not obtained in a calculation, an error must have been made somewhere. Careful inspection of units often reveals the source of the error.
SAMPLE EXERCISE 1.9 Converting Units
If a woman has a mass of 115 lb, what is her mass in grams? (Use the relationships between units given on the back inside cover of the text.)
SOLUTION
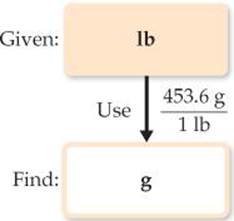
Because we want to change from pounds to grams, we look for a relationship between these units of mass. From the back inside cover we have 1 lb = 453.6 g. To cancel pounds and leave grams, we write the conversion factor with grams in the numerator and pounds in the denominator:
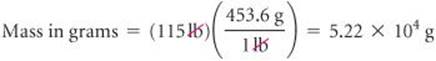
The answer can be given to only three significant figures, the number of significant figures in 115 lb. The process we have used is diagrammed in the margin.
PRACTICE EXERCISE
By using a conversion factor from the back inside cover, determine the length in kilometers of a 500.0-mi automobile race.
Answer: 804.7 km
 STRATEGIES IN CHEMISTRY
STRATEGIES IN CHEMISTRY
ESTIMATING ANSWERS
A friend once remarked cynically that calculators let you get the wrong answer more quickly. He was implying that unless you have the correct strategy for solving a problem and have punched in the correct numbers, the answer will be incorrect. If you learn to estimate answers, however, you will be able to check whether the answers to your calculations are reasonable.
The idea is to make a rough calculation using numbers that are rounded off in such a way that the arithmetic can be done without a calculator. This approach is often referred to as making a “ballpark” estimate, meaning that although it does not give an exact answer, it gives one that is roughly the right size. By using dimensional analysis and by estimating answers, we can readily check the reasonableness of our answers to calculations.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
How do we determine how many digits to use in conversion factors, such as the one between pounds and grams in Sample Exercise 1.9?
Using Two or More Conversion Factors
It is often necessary to use several conversion factors in solving a problem. As an example, let's convert the length of an 8.00-m rod to inches. The table on the back inside cover does not give the relationship between meters and inches. It does, however, give the relationship between centimeters and inches (1 in. = 2.54 cm). From our knowledge of SI prefixes, we know that 1 cm = 10–2. Thus, we can convert step by step, first from meters to centimeters and then from centimeters to inches:

Combining the given quantity (8.00 m) and the two conversion factors, we have
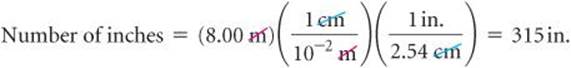
The first conversion factor is used to cancel meters and convert the length to centimeters. Thus, meters are written in the denominator and centimeters in the numerator. The second conversion factor is used to cancel centimeters and convert the length to inches, so it has centimeters in the denominator and inches, the desired unit, in the numerator.
Note that you could have used 100 cm = 1 m as a conversion factor as well in the second parentheses. As long as you follow your units and cancel them properly to obtain the desired units, you are likely to be successful in your calculations.
SAMPLE EXERCISE 1.10 Converting Units Using Two or More Conversion Factors
The average speed of a nitrogen molecule in air at 25 °C is 515m/s. Convert this speed to miles per hour.
SOLUTION
To go from the given units, m/s, to the desired units, mi/hr, we must convert meters to miles and seconds to hours. From our knowledge of SI prefixes we know that 1 km = 103m. From the relationships given on the back inside cover of the book, we find that 1 mi = 1.6093km.
Thus, we can convert m to km and then convert km to mi. From our knowledge of time we know that 60s = 1 min and 60 min = 1hr. Thus, we can convert s to min and then convert min to hr. The overall process is

Applying first the conversions for distance and then those for time, we can set up one long equation in which unwanted units are canceled:
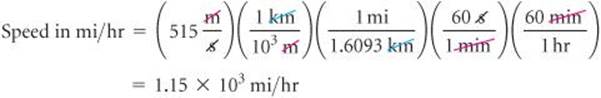
Our answer has the desired units. We can check our calculation, using the estimating procedure described in the “Strategies in Chemistry” box. The given speed is about 500m/s. Dividing by 1000 converts m to km, giving 0.5km/s. Because 1 mi is about 1.6 km, this speed corresponds to 0.5/1.6 = 0.3mi/s. Multiplying by 60 gives about 0.3 × 60 = 20mi/min. Multiplying again by 60 gives 20 × 60 = 1200mi/hr. The approximate solution (about 1200mi/hr) and the detailed solution (1150mi/hr) are reasonably close. The answer to the detailed solution has three significant figures, corresponding to the number of significant figures in the given speed in m/s.
PRACTICE EXERCISE
A car travels 28 mi per gallon of gasoline. How many kilometers per liter will it go?
Answer: 12 km/L
Conversions Involving Volume
The conversion factors previously noted convert from one unit of a given measure to another unit of the same measure, such as from length to length. We also have conversion factors that convert from one measure to a different one. The density of a substance, for example, can be treated as a conversion factor between mass and volume. Suppose we want to know the mass in grams of 2 cubic inches (2.00in.3) of gold, which has a density of 19.3g/cm3. The density gives us the conversion factor:
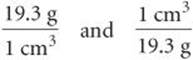
Because we want a mass in grams, we use the first factor, which has mass in grams in the numerator. To use this factor, however, we must first convert cubic inches to cubic centimeters. The relationship between in.3 and cm3 is not given on the back inside cover, but the relationship between inches and centimeters is given: 1 in = 2.54cm (exactly). Cubing both sides of this equation gives (1 in.)3 = (2.54cm)3, from which we write the desired conversion factor:
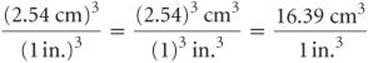
Notice that both the numbers and the units are cubed. Also, because 2.54 is an exact number, we can retain as many digits of (2.54)3 as we need. We have used four, one more than the number of digits in the density (19.3g/cm3). Applying our conversion factors, we can now solve the problem:
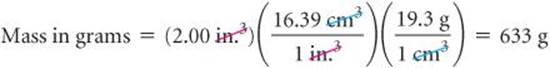
The procedure is diagrammed here. The final answer is reported to three significant figures, the same number of significant figures as in 2.00 in.3 and 19.3 g.

SAMPLE EXERCISE 1.11 Converting Volume Units
Earth's oceans contain approximately 1.36 × 109 km3 of water. Calculate the volume in liters.
SOLUTION
From the back inside cover, we find 1 L = 10–3 m3, but there is no relationship listed involving km3. From our knowledge of SI prefixes, however, we know 1 km = 103 and we can use this relationship between lengths to write the desired conversion factor between volumes:
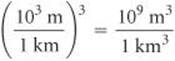
Thus, converting from km3 to m3 to L, we have
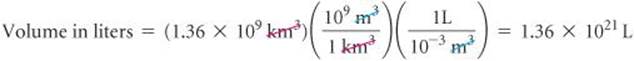
PRACTICE EXERCISE
If the volume of an object is reported as 5.0 ft3, what is the volume in cubic meters?
Answer: 0.14m3
 STRATEGIES IN CHEMISTRY
STRATEGIES IN CHEMISTRY
THE IMPORTANCE OF PRACTICE
If you have ever played a musical instrument or participated in athletics, you know that the keys to success are practice and discipline. You cannot learn to play a piano merely by listening to music, and you cannot learn how to play basketball merely by watching games on television. Likewise, you cannot learn chemistry by merely watching your instructor do it. Simply reading this book, listening to lectures, or reviewing notes will not usually be sufficient when exam time comes around. Your task is not only to understand how someone else does chemistry but also to be able to do it yourself. That takes practice on a regular basis, and anything that you have to do on a regular basis requires self-discipline until it becomes a habit.
Throughout the book, we have provided sample exercises in which the solutions are shown in detail. A practice exercise, for which only the answer is given, accompanies each sample exercise. It is important that you use these exercises as learning aids. End-of-chapter exercises provide additional questions to help you understand the material in the chapter. A review of basic mathematics is given in Appendix A.
The practice exercises in this text and the homework assignments given by your instructor provide the minimal practice that you will need to succeed in your chemistry course. Only by working all the assigned problems will you face the full range of difficulty and coverage that your instructor expects you to master for exams. There is no substitute for a determined and perhaps lengthy effort to work problems on your own. If you are stuck on a problem, however, ask for help from your instructor, a teaching assistant, a tutor, or a fellow student. Spending an inordinate amount of time on a single exercise is rarely effective unless you know that it is particularly challenging and requires extensive thought and effort.
SAMPLE EXERCISE 1.12 Conversions Involving Density
What is the mass in grams of 1.00 gal of water? The density of water is 1.00g/mL.
SOLUTION
Before we begin solving this exercise, we note the following:
1. We are given 1.00 gal of water (the known, or given, quantity) and asked to calculate its mass in grams (the unknown).
2. We have the following conversion factors either given, commonly known, or available on the back inside cover of the text:
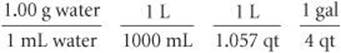
The first of these conversion factors must be used as written (with grams in the numerator) to give the desired result, whereas the last conversion factor must be inverted in order to cancel gallons:
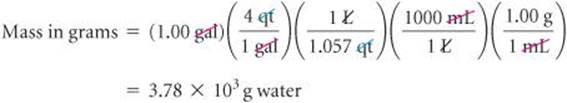
The unit of our final answer is appropriate, and we've taken care of our significant figures. We can further check our calculation by estimating. We can round 1.057 off to 1. Then focusing on the numbers that do not equal 1 gives 4 × 1000 = 4000g, in agreement with the detailed calculation.
You should also use common sense to assess the reasonableness of your answer. In this case we know that most people can lift a gallon of milk with one hand, although it would be tiring to carry it around all day. Milk is mostly water and will have a density not too different from that of water. Therefore, we might estimate that a gallon of water has mass that is more than 5 lb but less than 50 lb. The mass we have calculated, 3.78 kg × 2.2lb/kg = 8.3 lb, is thus reasonable as an order-of-magnitude estimate.
PRACTICE EXERCISE
The density of benzene is 0.879 g/mL. Calculate the mass in grams of 1.00 qt of benzene.
Answer: 832 g
 STRATEGIES IN CHEMISTRY
STRATEGIES IN CHEMISTRY
THE FEATURES OF THIS BOOK
To help you understand chemistry, this book includes features that help you organize your thoughts. At the beginning of each chapter, “What's Ahead,” which outlines the chapter by section, will prepare you for the material in the chapter. At the end of each chapter, the Summary, Key Terms, Key Skills, and Key Equations will help you remember what you have learned and prepare you for quizzes and exams.
During the course of the chapter, there are “speed bumps” to prompt you to think about what you have just read. The “Give It Some Thought” features are embedded in the text after a key concept; the “Go Figure” features are associated with artwork and ask you to interpret a concept visually. Sample Exercises, with worked-out solutions and answers, and Practice Exercises, which provide only the answer, test your problem-solving skills in chemistry.
At the end of each chapter is a series of exercises, again to test your problem-solving skills in chemistry. Your instructor will very likely assign some of these end-of-chapter exercises as homework. The first few exercises called “Visualizing Concepts” are meant to test how well you understand a concept without plugging a lot of numbers into a formula. The other exercises are divided into sections that reflect the order of the material in the chapter. These exercises are grouped in pairs, with the answers given in the back of the book to the odd-numbered exercises, as indicated by the red exercise numbers. An exercise with a [bracket] around its number means that it is more challenging. Additional Exercises appear after the regular exercises; the chapter sections that they cover are not identified, and they are not paired. Integrative Exercises, which start appearing in Chapter 3, are problems that require skills learned in previous chapters.
Throughout the book you will occasionally find little blue link [![]() ] symbols. These “concept links” tell you in which section of the book this concept is first discussed in case you wish to turn to that section and review it.
] symbols. These “concept links” tell you in which section of the book this concept is first discussed in case you wish to turn to that section and review it.
Throughout the book boxed essays highlight the importance of chemistry to our everyday lives. The “Chemistry and Life” boxes focus on biological and environmental aspects of chemistry. The “Chemistry Put to Work” boxes illustrate the large industrial role chemistry plays in modern society. “Strategies in Chemistry” boxes, like this one, are meant to help you think about the material you are learning. Finally, boxes entitled “A Closer Look” provide in-depth coverage of a key chemical concept.
Many chemical databases are available, usually through your school. The CRC Handbook of Chemistry and Physics is the standard reference for many types of data and is available in libraries. The Merck Index is a standard reference for the properties of many small organic compounds, especially ones of biological interest. WebElements (http://www.webelements.com) is a good Web site for looking up the properties of the elements.