CHEMISTRY THE CENTRAL SCIENCE
9 MOLECULAR GEOMETRY AND BONDING THEORIES
THE DRUG SHOWN HERE IS DIAZEPAM, better known as Valium. It is commonly prescribed for a wide range of disorders, including anxiety, insomnia, seizures, muscle spasms, restless legs syndrome, and obsessive-compulsive disorder. Valium was invented by Leo Sternbach at Hoffmann- LaRoche Pharmaceuticals and first licensed for use in 1960. It was the top-selling pharmaceutical in the United States from 1969 to 1982, with peak sales in 1978 of 2.3 billion tablets! It continues to be an important medication and is on the World Health Organization“s Essential Drugs list.
WHAT'S AHEAD
9.1 MOLECULAR SHAPES
We begin by discussing molecular shapes and examining some shapes commonly encountered in molecules.
9.2 THE VSEPR MODEL
We consider how molecular geometries can be predicted using the valence-shell electron-pair repulsion, or VSEPR, model, which is based on Lewis structures and the repulsions between regions of high electron density.
9.3 MOLECULAR SHAPE AND MOLECULAR POLARITY
Once we know the geometry of a molecule and the types of bonds it contains, we can determine whether the molecule is polar or nonpolar.
9.4 COVALENT BONDING AND ORBITAL OVERLAP
We recognize that electrons are shared between atoms in a covalent bond. In valence-bond theory, the bonding electrons are visualized as originating in atomic orbitals on two atoms. A covalent bond is formed when these orbitals overlap.
9.5 HYBRID ORBITALS
To account for molecular shape, we consider how the orbitals of one atom mix with one another, or hybridize, to create hybrid orbitals.
9.6 MULTIPLE BONDS
Atomic orbitals that contribute to covalent bonding in a molecule can overlap in multiple ways to produce sigma and pi bonds between atoms. Single bonds generally consist of one sigma bond; multiple bonds involve one sigma and one or more pi bonds. We examine the geometric arrangements of these bonds and how they are exemplified in organic Compounds.
9.7 MOLECULAR ORBITALS
We examine a more sophisticated treatment of bonding called molecular orbital theory, which introduces the concepts of bonding and antibonding molecular orbitals.
9.8 PERIOD 2 DIATOMIC MOLECULES
We consider how molecular orbital theory is used to construct energy-level diagrams for second-row diatomic molecules.
WE SAW IN CHAPTER 8 THAT LEWIS STRUCTURES help us understand the compositions of molecules and their covalent bonds. However, Lewis structures do not show one of the most important aspects of molecules—their overall shapes. The shape and size of molecules—sometimes referred to as molecular architecture––are defined by the angles and distances between the nuclei of the component atoms.
The shape and size of a molecule of a substance, together with the strength and polarity of its bonds, largely determine the properties of that substance. Some of the most dramatic examples of the important roles of molecular architecture are seen in biochemical reactions. For example, the chapter-opening photograph shows a molecular model of diazepam, better known as Valium. In the body, this relatively simple molecule enters into an extraordinary array of biochemical interactions. Valium works by binding to certain important sites in the central nervous system. Itseffectiveness is highly dependent on the shape and size of the molecule as well on the charge distributions within it. Even a small modification to molecular shape or size alters the drug's effectiveness.
One of our goals in this chapter is to develop a sense of the shapes of molecules and how those shapes are governed in large measure by the kinds of bonds that exist between the atoms making up the molecules.
Our first goal is to learn the relationship between two-dimensional Lewis structures and three-dimensional molecular shapes. Armed with this knowledge, we can examine the nature of covalent bonds. The lines used to depict bonds in Lewis structures provide important clues about the orbitals that molecules use in bonding. By examining these orbitals, we can gain a greater understanding of the behavior of molecules. Mastering the material in this chapter will help you in later discussions of the physical and chemical properties of substances.
9.1 MOLECULAR SHAPES
In Chapter 8 we used Lewis structures to account for the formulas of covalent compounds. 
(Section 8.5) Lewis structures, however, do not indicate the shapes of molecules; they simply show the number and types of bonds. For example, the Lewis structure of CCl4 tells us only that four Cl atoms are bonded to a central C atom:
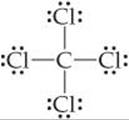
The Lewis structure is drawn with the atoms all in the same plane. As shown in 
FIGURE 9.1, however, the actual arrangement is the Cl atoms at the corners of a tetrahedron, a geometric object with four corners and four faces, each an equilateral triangle.
The shape of a molecule is determined by its bond angles, the angles made by the lines joining the nuclei of the atoms in the molecule. The bond angles of a molecule, together with the bond lengths (Section 8.8), define the shape and size of the molecule. In Figure 9.1, you should be able to see that there are six Cl—C—Cl bond angles in CCl4 and that they all have the same value of 109.5°, the angle size characteristic of a tetrahedron. In addition, all four C—Cl bonds are the same length (1.78 Å). Thus, the shape and size of CCl4 are completely described by stating that the molecule is tetrahedral with C—Cl bonds of length 1.78 Å.
We begin our discussion of molecular shapes with molecules (and ions) that, like CCl4, have a single central atom bonded to two or more atoms of the same type. Such molecules have the general formula ABn in which the central atom A is bonded to n
GO FIGURE
In the space-filling model, what determines the relative sizes of the spheres?
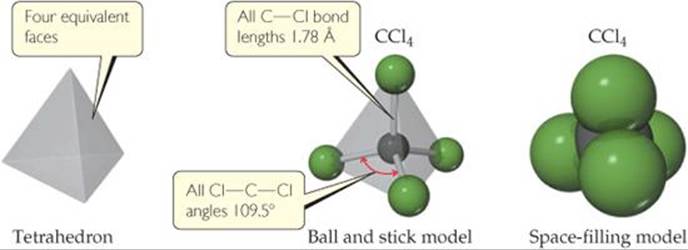
FIGURE 9.1 Tetrahedral shape of CCl4.
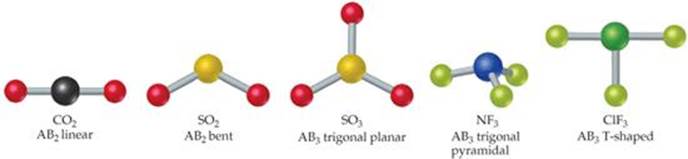
FIGURE 9.2 Shapes of AB2 and AB3 molecules.
B atoms. Both CO2 and H2O are AB2 molecules, for example, whereas SO3 and NH3 are AB3 molecules, and so on.
The number of shapes possible for ABn molecules depends on the value of n. Those commonly found for AB2 and AB3 molecules are shown in FIGURE 9.2. An AB2 molecule must be either linear (bond angle = 180°) or bent (bond angle ≠ 180°). For AB3 molecules, the two most common shapes place the B atoms at the corners of an equilateral triangle. If the A atom lies in the same plane as the B atoms, the shape is trigonal planar. If the A atom lies above the plane of the B atoms, the shape is trigonal pyramidal (a pyramid with an equilateral triangle as its base). Some AB3 molecules, such as ClF3, are T-shaped, the relatively unusual shape shown in Figure 9.2. The atoms lie in one plane, but the angles between them vary as shown.
Compare Figures 9.1 and 9.2 to notice the difference between NF3 and CCl4. The CCl4 molecule is tetrahedral because the four atoms bonded to the carbon are disposed at the four apexes of a tetrahedron around the central atom. The NF3 molecule is pyramidal because the three atoms bonded to nitrogen lie at the base of a trigonal pyramid.
The shapes that maximize the separation of outer atoms are shown in 
FIGURE 9.3. In addition to the shapes we have already seen, this figure shows those encountered when there are five or six atoms surrounding a central atom. The trigonal bipyramid can be thought of as two face-to-face trigonal pyramids; the octahedron is like two face-to-face square pyramids.
GO FIGURE
Which of these molecular shapes do you expect for the SF6 molecule?
FIGURE 9.3 Shapes allowing maximum distances between atoms in ABn molecules.
FIGURE 9.4 Derivatives of the tetrahedral molecular shape.
FIGURE 9.5 A balloon analogy for electron domains.
Some molecules have shapes other than those shown in Figure 9.3, but we can usually derive the shape of those molecules from Figure 9.3. Neither trigonal pyramidal nor bent is shown in Figure 9.3, for instance, but FIGURE 9.4 shows how we can arrive at these shapes by removing atoms from the tetrahedral shape.
Why do so many ABn molecules have shapes related to those shown in Figure 9.3, and can we predict these shapes? When A is a representative element (one from the s block or p block of the periodic table), we can answer these questions by using the valence-shell electron-pair repulsion (VSEPR) model. Although the name is rather imposing, the model is quite simple. It has useful predictive capabilities, as we will see in Section 9.2.
GIVE IT SOME THOUGHT
In addition to tetrahedral, another common shape for AB4 molecules is square planar. All five atoms lie in the same plane, with the B atoms at the corners of a square and the A atom at the center of the square. Which shape in Figure 9.3 could lead to a square-planar shape upon removal of one or more atoms?