CHEMISTRY THE CENTRAL SCIENCE

10 GASES

10.2 PRESSURE

In everyday terms, pressure conveys the idea of force, a push that tends to move something in a given direction. Pressure, P, is defined in science as the force, F, that acts on a given area, A.

Gases exert a pressure on any surface with which they are in contact. The gas in an inflated balloon, for example, exerts a pressure on the inside surface of the balloon.

Atmospheric Pressure and the Barometer

People, coconuts, and nitrogen molecules all experience an attractive gravitational force that pulls them toward the center of Earth. When a coconut comes loose from a tree, for example, this force causes the coconut to be accelerated toward Earth, its speed increasing as its potential energy is converted into kinetic energy. (Section 5.1) The gas atoms and molecules of the atmosphere also experience a gravitational acceleration. Because these particles have such tiny masses, however, their thermal energies of motion (their kinetic energies) override the gravitational forces, so the particles that make up the atmosphere don't pile up at Earths surface. Nevertheless, the gravitational force does operate, and it causes the atmosphere as a whole to press down on Earth's surface, creating atmospheric pressure, defined as the force exerted by the atmosphere on a given surface area.

You can demonstrate the existence of atmospheric pressure with an empty plastic water bottle. If you suck on the mouth of the empty bottle, chances are you can cause the bottle to partially cave in. When you break the partial vacuum you have created, the bottle pops out to its original shape. The bottle caves in because, once you've sucked out some of the air molecules, air molecules in the atmosphere exert a force on the outside of the bottle that is greater than the force exerted by the lesser number of air molecules inside the bottle. We calculate the magnitude of this atmospheric pressure as follows: The force, F, exerted by any object is the product of its mass, m, and its acceleration, a: F = ma. The acceleration given by Earth's gravitational force to any object located near Earth's surface is 9.8 m/s². Now imagine a column of air 1 m² in cross section extending through the entire atmosphere (FIGURE 10.1). That column has a mass of roughly 10,000 kg. The downward gravitational force exerted on this column is

F = (10,000 kg)(9.8 m/s²) = 1 × 10⁵ kg-m/s² = 1 × 10⁵ N

where N is the abbreviation for newton, the SI unit for force: 1 N = 1 kg-m/s². The pressure exerted by the column is this force divided by the cross-sectional area, A, over which the force is applied. Because our air column has a cross-sectional area of 1 m², we have for the magnitude of atmospheric pressure at sea level

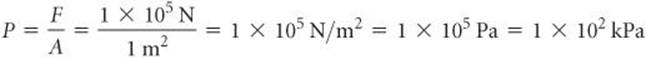
The SI unit of pressure is the pascal (Pa), named for Blaise Pascal (1623–1662), a French scientist who studied pressure: 1 Pa = 1 N/m². A related pressure unit is the bar: 1 bar = 10⁵ Pa = 105 N/m². Thus, the atmospheric pressure at sea level we just calculated, 100 kPa, can be reported as 1 bar. (The actual atmospheric pressure at any location depends on weather conditions and altitude.) Another pressure unit is pounds per square inch (psi, lbs/in.²). At sea level, atmospheric pressure is 14.7 psi.

GIVE IT SOME THOUGHT

Assume the top of your head has a surface area of 10 in. × 10 in. How many pounds of air are you carrying on your head if you are at sea level?

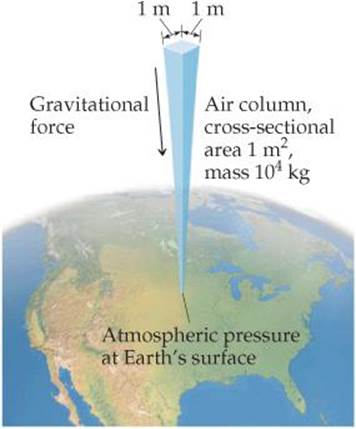
FIGURE 10.1 Calculating atmospheric pressure.

In the seventeenth century many scientists and philosophers believed that the atmosphere had no weight. Evangelista Torricelli (1608–1647), a student of Galileo's, proved this untrue. He invented the barometer (FIGURE 10.2), which is made from a glass tube more than 760 mm long that is closed at one end, completely filled with mercury, and inverted into a dish of mercury. (Care must be taken so that no air gets into the tube.) When the tube is inverted into the dish, some of the mercury flows out of the tube, but a column of mercury remains in the tube. Torricelli argued that the mercury surface in the dish experiences the full force of Earths atmosphere, which pushes the mercury up the tube until the pressure exerted by the mercury column downward, due to gravity, equals the atmospheric pressure at the base of the tube. Therefore the height, h, of the mercury column is a measure of atmospheric pressure and changes as atmospheric pressure changes.

GO FIGURE

What happens to h, the height of the mercury column, if the atmospheric pressure increases?

FIGURE 10.2 A mercury barometer.

Although Torricelli's explanation met with fierce opposition, it also had supporters. Blaise Pascal, for example, had one of Torricelli's barometers carried to the top of a mountain and compared its reading there with the reading on a duplicate barometer at the base of the mountain. As the barometer was carried up, the height of the mercury column diminished, as expected, because the amount of atmosphere pressing down on the mercury in the dish decreased as the instrument was carried higher. These and other experiments eventually prevailed, and the idea that the atmosphere has weight became accepted.

Standard atmospheric pressure, which corresponds to the typical pressure at sea level, is the pressure sufficient to support a column of mercury 760 mm high. In SI units this pressure is 1.01325 × 10⁵ Pa. Standard atmospheric pressure defines some common non-SI units used to express gas pressure, such as the atmosphere (atm) and the millimeter of mercury (mm Hg). The latter unit is also called the torr, after Torricelli: 1 torr = 1 mm Hg. Thus, we have

1 atm = 760. mm Hg = 760. torr = 1.01325 × 10⁵ Pa = 101.325 kPa = 1.01325 bar

We will usually express gas pressure in atmospheres, pascals, kilopascals, or torr, so you should be comfortable converting pressures from one unit to another.

SAMPLE EXERCISE 10.1 Converting Pressure Units

(a) Convert 0.357 atm to torr. (b) Convert 6.6 × 10^–2 torr to atmospheres. (c) Convert 147.2 kPa to torr.

SOLUTION

Analyze In each case we are given the pressure in one unit and asked to convert it to another unit. Our task, therefore, is to choose the appropriate conversion factors.

Plan We can use dimensional analysis to perform the desired conversions.

Solve

(a) To convert atmospheres to torr, we use the relationship 760 torr = 1 atm:

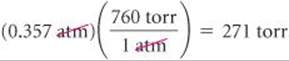
Note that the units cancel in the required manner.

(b) We use the same relationship as in part (a). To get the appropriate units to cancel, we must use the conversion factor as follows:

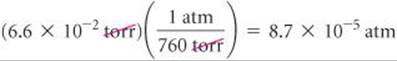
(c) The relationship 760 torr = 101.325 kPa allows us to write an appropriate conversion factor for this problem:

Check In each case, compare the magnitude of the answer with the starting value. The torr is a much smaller unit than the atmosphere (since there are 760 torr in 1 atm), so we expect the numerical answer to be larger than the starting quantity in (a) and smaller in (b). In (c) notice that there are nearly 8 torr per kPa, so the numerical answer in torr should be about eight times larger than its value in kPa, consistent with our calculation.

PRACTICE EXERCISE

(a) In countries that use the metric system, atmospheric pressure in weather reports is given in kilopascals. Convert a pressure of 745 torr to kilopascals. (b) The pressure at the center of Hurricane Katrina was 902 mbar (millibars). There are 1000 mbar in 1 bar; convert this pressure to atmospheres.

Answers: (a) 99.3 kPa, (b) 0.890 atm

We use various devices to measure the pressures of enclosed gases. Tire gauges, for example, measure the pressure of air in automobile and bicycle tires. In laboratories we sometimes use a manometer, which operates on a principle similar to that of a barometer, as shown in Sample Exercise 10.2.

SAMPLE EXERCISE 10.2 Using a Manometer to Measure Gas Pressure

On a certain day a laboratory barometer indicates that the atmospheric pressure is 764.7 torr. A sample of gas is placed in a flask attached to an open-end mercury manometer (FIGURE 10.3), and a meter stick is used to measure the height of the mercury in the two arms of the U tube. The height of the mercury in the open-end arm is 136.4 mm, and the height in the arm in contact with the gas in the flask is 103.8 mm. What is the pressure of the gas in the flask (a) in atmospheres, (b) in kilopascals?

SOLUTION

Analyze We are given the atmospheric pressure (764.7 torr) and the mercury heights in the two arms of the manometer and asked to determine the gas pressure in the flask. Recall that millimeters of mercury is a pressure unit. We know that the gas pressure from the flask must be greater than atmospheric pressure because the mercury level in the arm on the flask side (103.8 mm) is lower than the level in the arm open to the atmosphere (136.4 mm). Therefore, the gas from the flask is pushing mercury from the arm in contact with the flask into the arm open to the atmosphere.

Plan We will use the difference in height between the two arms (h in Figure 10.3) to obtain the amount by which the pressure of the gas exceeds atmospheric pressure. Because an open-end mercury manometer is used, the height difference directly measures the pressure difference in mm Hg or torr between the gas and the atmosphere.

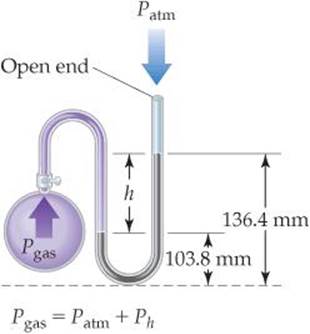
FIGURE 10.3 A mercury manometer.

Solve

(a) The pressure of the gas equals the atmospheric pressure plus h:

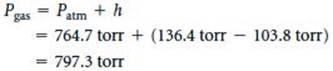
We convert the pressure of the gas to atmospheres:

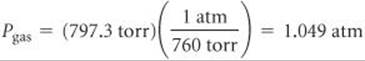
(b) To calculate the pressure in kPa, we employ the conversion factor between atmospheres and kPa:

Check The calculated pressure is a bit more than 1 atm, which is about 101 kPa. This makes sense because we anticipated that the pressure in the flask would be greater than the atmospheric pressure (764.7 torr = 1.01 atm) acting on the manometer.

PRACTICE EXERCISE

Convert a pressure of 0.975 atm into Pa and kPa.

Answers: 9.88 × 10⁴ Pa and 98.8 kPa