CHEMISTRY THE CENTRAL SCIENCE
10 GASES
10.5 FURTHER APPLICATIONS OF THE IDEAL-GAS EQUATION
In this section, we use the ideal-gas equation first to define the relationship between the density of a gas and its molar mass, and then to calculate the volumes of gases formed or consumed in chemical reactions.
Gas Densities and Molar Mass
Recall that density has units of mass per unit volume (d = m/V). ![]() (Section 1.4) We can arrange the ideal-gas equation to obtain the similar units of moles per unit volume:
(Section 1.4) We can arrange the ideal-gas equation to obtain the similar units of moles per unit volume:
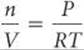
If we multiply both sides of this equation by the molar mass, M, which is the number of grams in 1 mol of a substance, we obtain

The term on the left equals the density in grams per liter:
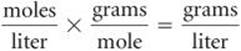
Thus, the density of the gas is also given by the expression on the right in Equation 10.9:

This equation tells us that the density of a gas depends on its pressure, molar mass, and temperature. The higher the molar mass and pressure, the denser the gas. The higher the temperature, the less dense the gas. Although gases form homogeneous mixtures, a less dense gas will lie above a denser gas in the absence of mixing. For example, CO2 has a higher molar mass than N2 or O2 and is therefore denser than air. For this reason, CO2 released from a CO2 fire extinguisher blankets a fire, preventing O2 from reaching the combustible material. “Dry ice,” which is solid CO2, converts directly to CO2 gas at room temperature, and the resulting “fog” (which is actually condensed water droplets cooled by the CO2) flows downhill in air (![]() FIGURE 10.12).
FIGURE 10.12).

![]() FIGURE 10.12 Carbon dioxide gas flows downhill because it is denser than air. The CO2 “fog” is not the gas made visible but rather is made up of drops of water that have condensed from water vapor in the air.
FIGURE 10.12 Carbon dioxide gas flows downhill because it is denser than air. The CO2 “fog” is not the gas made visible but rather is made up of drops of water that have condensed from water vapor in the air.
When we have equal molar masses of two gases at the same pressure but different temperatures, the hotter gas is less dense than the cooler one, so the hotter gas rises. The difference between the densities of hot and cold air is responsible for the lift of hot-air balloons. It is also responsible for many phenomena in weather, such as the formation of large thunderhead clouds during thunderstorms.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Is water vapor more or less dense than N2 under the same conditions of temperature and pressure?
SAMPLE EXERCISE 10.7 Calculating Gas Density
What is the density of carbon tetrachloride vapor at 714 torr and 125 °C?
SOLUTION
Analyze We are asked to calculate the density of a gas given its name, its pressure, and its temperature. From the name we can write the chemical formula of the substance and determine its molar mass.
Plan We can use Equation 10.10 to calculate the density. Before we can do that, however, we must convert the given quantities to the appropriate units, degrees Celsius to kelvins and pressure to atmospheres. We must also calculate the molar mass of CCl4.
Solve The absolute temperature is 125 + 273 = 398 K. The pressure is (714 torr) (1 atm/760 torr) = 0.939 atm. The molar mass of CCl4 is 12.01 + (4) (35.45) = 153.8 g/mol. Therefore,
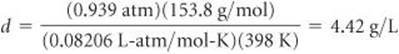
Check If we divide molar mass (g/mol) by density (g/L), we end up with L/mol. The numerical value is roughly 154/4.4 = 35. That is in the right ballpark for the molar volume of a gas heated to 125 °C at near atmospheric pressure, so our answer is reasonable.
PRACTICE EXERCISE
The mean molar mass of the atmosphere at the surface of Titan, Saturn's largest moon, is 28.6 g/mol. The surface temperature is 95 K, and the pressure is 1.6 atm. Assuming ideal behavior, calculate the density of Titan's atmosphere.
Answer: 5.9 g/L
Equation 10.10 can be rearranged to solve for the molar mass of a gas:

Thus, we can use the experimentally measured density of a gas to determine the molar mass of the gas molecules, as shown in Sample Exercise 10.8.
SAMPLE EXERCISE 10.8 Calculating the Molar Mass of a Gas
A large evacuated flask initially has a mass of 134.567 g. When the flask is filled with a gas of unknown molar mass to a pressure of 735 torr at 31 °C, its mass is 137.456 g. When the flask is evacuated again and then filled with water at 31 °C, its mass is 1067.9 g. (The density of water at this temperature is 0.997 g/mL.) Assuming the ideal-gas equation applies, calculate the molar mass of the gas.
SOLUTION
Analyze We are given the temperature (31 °C) and pressure (735 torr) for a gas, together with information to determine its volume and mass, and we are asked to calculate its molar mass.
Plan We need to use the mass information given to calculate the volume of the container and the mass of the gas in it. From this we calculate the gas density and then apply Equation 10.11 to calculate the molar mass of the gas.
Solve The gas mass is the difference between the mass of the flask filled with gas and the mass of the evacuated flask:
137.456 g – 134.567 g = 2.889 g
The gas volume equals the volume of water the flask can hold, calculated from the mass and density of the water. The mass of the water is the difference between the masses of the full and evacuated flask:
1067.9 g – 134.567 g = 933.3 g
Rearranging the equation for density (d = m/V), we have
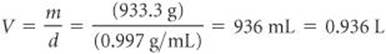
Knowing the mass of the gas (2.889 g) and its volume (0.936 L), we can calculate the density of the gas:
2.889 g/0.936 L = 3.09 g/L
After converting pressure to atmospheres and temperature to kelvins, we can use Equation 10.11 to calculate the molar mass:

Check The units work out appropriately, and the value of molar mass obtained is reasonable for a substance that is gaseous near room temperature.
PRACTICE EXERCISE
Calculate the average molar mass of dry air if it has a density of 1.17 g/L at 21 °C and 740.0 torr.
Answer: 29.0 g/mol
Volumes of Gases in Chemical Reactions
We are often concerned with knowing the identity and/or quantity of a gas involved in a chemical reaction. Thus, it is useful to be able to calculate the volumes of gases consumed or produced in reactions. Such calculations are based on the mole concept and balanced chemical equations. ![]() (Section 3.6) The coefficients in a balanced chemical equation tell us the relative amounts (in moles) of reactants and products in a reaction. The ideal-gas equation relates the number of moles of a gas to P, V, and T.
(Section 3.6) The coefficients in a balanced chemical equation tell us the relative amounts (in moles) of reactants and products in a reaction. The ideal-gas equation relates the number of moles of a gas to P, V, and T.
 CHEMISTRY PUT TO WORK
CHEMISTRY PUT TO WORK
Gas Pipelines
Throughout the developed world, mostly invisible underground pipelines move massive quantities of liquids and gases over hundreds of miles. Essentially all substances that are gases at STP are transported commercially by pipeline, but the largest volume transported by far is natural gas (![]() FIGURE 10.13). This methane-rich gas from oil and gas wells is processed to remove particulates, water, and various gaseous impurities such as hydrogen sulfide and carbon dioxide. The gas is then compressed to pressures ranging from 3.5 MPa (35 atm) to 10 MPa (100 atm), depending on the age and diameter of the pipe. Large compressor stations along the pipeline, spaced at 50- to 100-mile intervals, maintain pressure.
FIGURE 10.13). This methane-rich gas from oil and gas wells is processed to remove particulates, water, and various gaseous impurities such as hydrogen sulfide and carbon dioxide. The gas is then compressed to pressures ranging from 3.5 MPa (35 atm) to 10 MPa (100 atm), depending on the age and diameter of the pipe. Large compressor stations along the pipeline, spaced at 50- to 100-mile intervals, maintain pressure.
Recall from Figure 5.25 that natural gas is a major source of energy for the United States. To meet this demand, methane must be transported from source wells throughout the United States and Canada to all parts of the nation. The total length of pipeline for natural-gas transport in the United States is about 6 × 105 km and growing. The United States is divided into seven regions. The total deliverability of natural gas to the seven regions exceeds 2.7 × 1012 L (measured at STP), almost 100 billion cubic feet per day! The total pipeline volume is not large enough for the enormous quantities of natural gas placed into and taken out of the system on a continuing basis. For this reason, underground storage facilities, such as salt caverns and other natural formations, are employed to hold large quantities of gas.
RELATED EXERCISE: 10.126
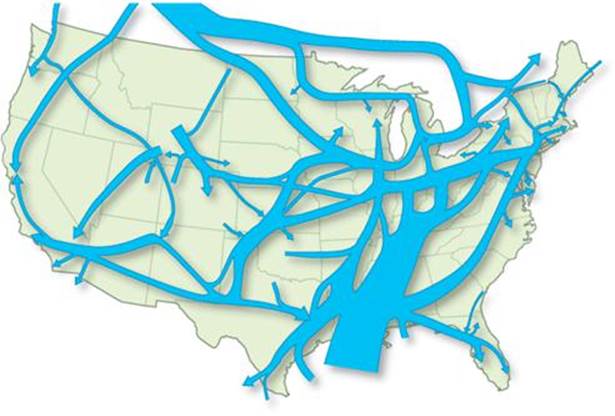
![]() FIGURE 10.13 Natural gas pipeline network in the United States. The thickest arrow represents flow of 15,000 million cubic feet of gas per day; the thinnest arrow represents flow of 1000 million cubic feet per day.
FIGURE 10.13 Natural gas pipeline network in the United States. The thickest arrow represents flow of 15,000 million cubic feet of gas per day; the thinnest arrow represents flow of 1000 million cubic feet per day.
SAMPLE EXERCISE 10.9 Relating a Gas Volume to the Amount of Another Substance in a Reaction
Automobile air bags are inflated by nitrogen gas generated by the rapid decomposition of sodium azide, NaN3:
2 NaN3(s) → Na(s) + 3 N2(g)
SOLUTION
Analyze This is a multistep problem. We are given the volume, pressure, and temperature of the N2 gas and the chemical equation for the reaction by which the N2 is generated. We must use this information to calculate the number of grams of NaN3 needed to obtain the necessary N2.
If an air bag has a volume of 36 L and is to be filled with nitrogen gas at 1.15 atm and 26.0 °C, how many grams of NaN3 must be decomposed?
Plan We need to use the gas data (P, V, and T) and the ideal-gas equation to calculate the number of moles of N2 gas that should be formed for the air bag to operate correctly. We can then use the balanced equation to determine the number of moles of NaN3 needed. Finally, we can convert moles of NaN3 to grams.

Solve The number of moles of N2 is determined using the ideal-gas equation:
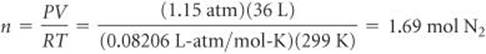
We use the coefficients in the balanced equation to calculate the number of moles of NaN3:
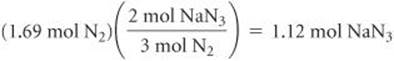
Finally, using the molar mass of NaN3, we convert moles of NaN3 to grams:
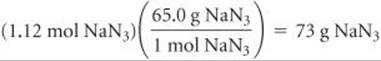
Check The units cancel properly at each step in the calculation, leaving us with the correct units in the answer, g NaN3.
PRACTICE EXERCISE
In the first step in the industrial process for making nitric acid, ammonia reacts with oxygen in the presence of a suitable catalyst to form nitric oxide and water vapor:
4 NH3(g) + 5 O2(g) → NO(g) + 6 H2O(g)
How many liters of NH3(g) at 850 °C and 5.00 atm are required to react with 1.00 mol of O2(g) in this reaction?
Answer: 14.8 L