CHEMISTRY THE CENTRAL SCIENCE
10 GASES
10.7 THE KINETIC-MOLECULAR THEORY OF GASES
The ideal-gas equation describes how gases behave but not why they behave as they do. Why does a gas expand when heated at constant pressure? Or why does its pressure increase when the gas is compressed at constant temperature? To understand the physical properties of gases, we need a model that helps us picture what happens to gas particles when conditions such as pressure or temperature change. Such a model, known as the kinetic-molecular theory of gases, was developed over a period of about 100 years, culminating in 1857 when Rudolf Clausius (1822–1888) published a complete and satisfactory form of the theory.
The kinetic-molecular theory (the theory of moving molecules) is summarized by the following statements:
1. Gases consist of large numbers of molecules that are in continuous, random motion. (The word molecule is used here to designate the smallest particle of any gas even though some gases, such as the noble gases, consist of individual atoms. All we learn about gas behavior from the kinetic-molecular theory applies equally to atomic gases.)
2. The combined volume of all the molecules of the gas is negligible relative to the total volume in which the gas is contained.
3. Attractive and repulsive forces between gas molecules are negligible.
4. Energy can be transferred between molecules during collisions but, as long as temperature remains constant, the average kinetic energy of the molecules does not change with time.
5. The average kinetic energy of the molecules is proportional to the absolute temperature. At any given temperature the molecules of all gases have the same average kinetic energy.
The kinetic-molecular theory explains both pressure and temperature at the molecular level. The pressure of a gas is caused by collisions of the molecules with the walls of the container (
FIGURE 10.16). The magnitude of the pressure is determined by how often and how forcefully the molecules strike the walls.
The absolute temperature of a gas is a measure of the average kinetic energy of its molecules. If two gases are at the same temperature, their molecules have the same average kinetic energy (statement 5 of the kinetic-molecular theory). If the absolute temperature of a gas is doubled, the average kinetic energy of its molecules doubles. Thus, molecular motion increases with increasing temperature.
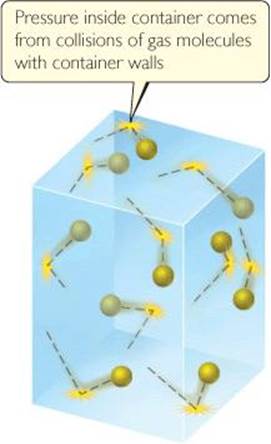
FIGURE 10.16 The molecular origin of gas pressure.
Distributions of Molecular Speed
Although collectively the molecules in a sample of gas have an average kinetic energy and hence an average speed, the individual molecules are moving at different speeds. Each molecule collides frequently with other molecules. Momentum is conserved in each collision, but one of the colliding molecules might be deflected off at high speed while the other is nearly stopped. The result is that, at any instant, the molecules in the sample have a wide range of speeds. In 
FIGURE 10.17 (a), which shows the distribution of molecular speeds for nitrogen gas at 0 °C and 100 °C, we see that a larger fraction of the 100 °C molecules moves at the higher speeds. This means that the 100 °C sample has the higher average kinetic energy.
GO FIGURE
Estimate the fraction of molecules at 100 °C with speeds less than 300 m/s.
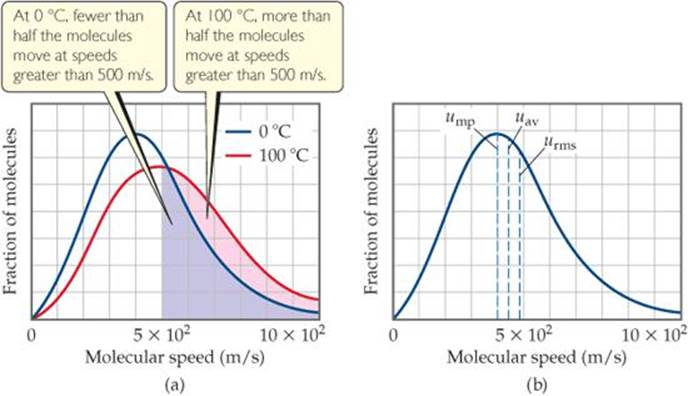
FIGURE 10.17 Distribution of molecular speeds for nitrogen gas. (a) The effect of temperature on molecular speed. The relative area under the curve for a range of speeds gives the relative fraction of molecules that have those speed. (b) Position of most probable (ump), average (uav), and root-mean-square (urms) speeds of gas molecules. The data shown here are for nitrogen gas at 0 °C.
In any graph of the distribution of molecular speeds in a gas sample, the peak of the curve represents the most probable speed, ump, which is the speed of the largest number of molecules [Figure 10.17(b)]. The most probable speeds in Figure 10.17(a), for instance, are 4 × 102 m/s for the 0 °C sample and 5 × 102 m/s for the 100 °C sample. Figure 10.17(b) also shows the root-mean-square (rms) speed, urms, of the molecules. This is the speed of a molecule possessing a kinetic energy identical to the average kinetic energy of the sample. The rms speed is not quite the same as the average (mean) speed, uav. The difference between the two is small, however. In Figure 10.17(b), for example, the root-mean-square speed is almost 5 × 102m/s and the average speed is about 4.5 × 102 m/s.
If you calculate the rms speeds as we will in Section 10.8, you will find that the rms speed is almost 6 × 102 m/s for the 100 °C sample but slightly less than 5 × 102 m/s for the 0 °C sample. Notice that the distribution curve broadens as we go to a higher temperature, which tells us that the range of molecular speeds increases with temperature.
The rms speed is important because the average kinetic energy of the gas molecules in a sample is equal to 
m(urms)2. 
(Section 5.1) Because mass does not change with temperature, the increase in the average kinetic energy ½ m(urms)2 as the temperature increases implies that the rms speed of the molecules (as well as their average speed) increases as temperature increases.
GIVE IT SOME THOUGHT
Consider three gases all at 298 K: HCl, H2, and O2. List the gases in order of increasing average speed.
Application of Kinetic-Molecular Theory to the Gas Laws
The empirical observations of gas properties as expressed by the various gas laws are readily understood in terms of the kinetic-molecular theory. The following examples illustrate this point:
1. An increase in volume at constant temperature causes pressure to decrease. A constant temperature means that the average kinetic energy of the gas molecules remains unchanged. This means that the rms speed of the molecules remains unchanged. When the volume is increased, the molecules must move a longer distance between collisions. Consequently, there are fewer collisions per unit time with the container walls, which means the pressure decreases. Thus, kinetic-molecular theory explains Boyle's law.
2. A temperature increase at constant volume causes pressure to increase. An increase in temperature means an increase in the average kinetic energy of the molecules and in u rms. Because there is no change in volume, the temperature increase causes more collisions with the walls per unit time because the molecules are all moving faster. Furthermore, the momentum in each collision increases (the molecules strike the walls more forcefully). A greater number of more forceful collisions means the pressure increases, and the theory explains this increase.
SAMPLE EXERCISE 10.13 Applying the Kinetic-Molecular Theory
A sample of O2 gas initially at STP is compressed to a smaller volume at constant temperature. What effect does this change have on (a) the average kinetic energy of the molecules, (b) their average speed, (c) the number of collisions they make with the container walls per unit time, (d) the number of collisions they make with a unit area of container wall per unit time?
SOLUTION
Analyze We need to apply the concepts of the kinetic-molecular theory of gases to a gas compressed at constant temperature.
Plan We will determine how each of the quantities in (a)–(d) is affected by the change in volume at constant temperature.
A CLOSER LOOK
THE IDEAL-GAS EQUATION
The ideal-gas equation can be derived from the five statements given in the text for the kinetic-molecular theory. Rather than perform the derivation, however, let's consider in qualitative terms how the ideal-gas equation might follow from these statements. The total force of the molecular collisions on the walls and hence the pressure (force per unit area, Section 10.2) produced by these collisions depend both on how strongly the molecules strike the walls (impulse imparted per collision) and on the rate at which the collisions occur:
P α impulse imparted per collision × collision rate
For a molecule traveling at the rms speed, the impulse imparted by a collision with a wall depends on the momentum of the molecule; that is, it depends on the product of the molecule's mass and speed: murms. The collision rate is proportional to the number of molecules per unit volume, n/V, and to their speed, which is urms because we are talking about only molecules traveling at this speed. If there are more molecules in a container, there will be more frequent collisions with the walls. As the molecular speed increases or the container volume decreases, the time required for molecules to travel from one wall to another is reduced, and the molecules collide more frequently with the walls. Thus, we have
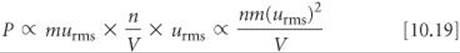
Because the average kinetic energy, 
m(urms)2, is proportional to temperature, we have m(urms)2 α T. Making this substitution in Equation 10.19 gives
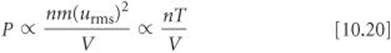
If we put in a proportionality constant, calling it R, the gas constant, you can see that we obtain the ideal-gas equation:
Swiss mathematician Daniel Bernoulli (1700–1782) conceived of a model for gases that was, for all practical purposes, the same as the model described by the kinetic-molecular theory of gases. From this model, Bernoulli derived Boyle's law and the ideal-gas equation. His was one of the first examples in science of developing a mathematical model from a set of assumptions, or hypothetical statements. However, Bernoulli's work on this subject was completely ignored, only to be rediscovered a hundred years later by Clausius and others. It was ignored because it conflicted with popular beliefs and was in conflict with Isaac Newton's incorrect model for gases. Those idols of the times had to fall before the way was clear for the kinetic-molecular theory. As this story illustrates, science is not a straight road running from here to the “truth.” The road is built by humans, so it zigs and zags.
RELATED EXERCISES: 10.77, 10.78, 10.79, and 10.80
Solve (a) Because the average kinetic energy of the O2 molecules is determined only by temperature, this energy is unchanged by the compression. (b) Because the average kinetic energy of the molecules does not change, their average speed remains constant. (c) The number of collisions with the walls per unit time increases because the molecules are moving in a smaller volume but with the same average speed as before. Under these conditions they must encounter a wall more frequently. (d) The number of collisions with a unit area of wall per unit time increases because the total number of collisions with the walls per unit time increases and the area of the walls decreases.
Check In a conceptual exercise of this kind, there is no numerical answer to check. All we can check in such cases is our reasoning in the course of solving the problem.
PRACTICE EXERCISE
How is the rms speed of N2 molecules in a gas sample changed by (a) an increase in temperature, (b) an increase in volume, (c) mixing with a sample of Ar at the same temperature?
Answers: (a) increases, (b) no effect, (c) no effect