CHEMISTRY THE CENTRAL SCIENCE
10 GASES
10.9 REAL GASES: DEVIATIONS FROM IDEAL BEHAVIOR
The extent to which a real gas departs from ideal behavior can be seen by rearranging the ideal-gas equation to solve for n:

This form of the equation tells us that for 1 mol of ideal gas, the quantity PV/RT equals 1 at all pressures. In ![]() FIGURE 10.22 PV/RT is plotted as a function of P for 1 mol of several real gases. At high pressures (generally above 10 atm) the deviation from ideal behavior (PV/RT = 1) is large and different for each gas. Real gases, in other words, do not behave ideally at high pressure. At lower pressures (usually below 10 atm), however, the deviation from ideal behavior is small, and we can use the ideal-gas equation without generating serious error.
FIGURE 10.22 PV/RT is plotted as a function of P for 1 mol of several real gases. At high pressures (generally above 10 atm) the deviation from ideal behavior (PV/RT = 1) is large and different for each gas. Real gases, in other words, do not behave ideally at high pressure. At lower pressures (usually below 10 atm), however, the deviation from ideal behavior is small, and we can use the ideal-gas equation without generating serious error.
![]() GO FIGURE
GO FIGURE
Does molar mass correlate with nonideal-gas behavior below 200 atm?
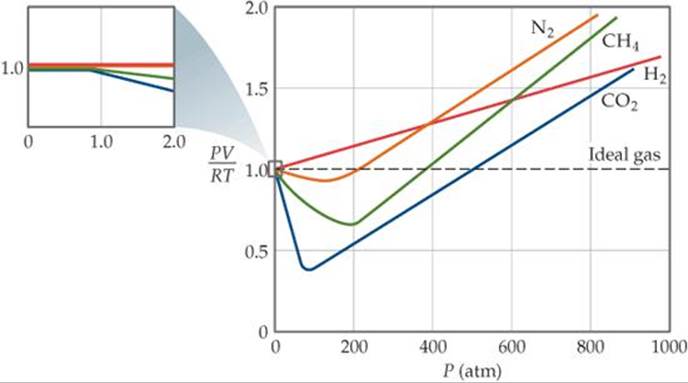
![]() FIGURE 10.22 The effect of pressure on the behavior of several real gases. Data for 1 mol of gas in all cases. Data for N2, CH4, and H2 are at 300 K; for CO2 data are at 313 K because under high pressure CO2 liquefies at 300 K.
FIGURE 10.22 The effect of pressure on the behavior of several real gases. Data for 1 mol of gas in all cases. Data for N2, CH4, and H2 are at 300 K; for CO2 data are at 313 K because under high pressure CO2 liquefies at 300 K.
![]() GO FIGURE
GO FIGURE
True or false: Nitrogen gas behaves more like an ideal gas as the temperature increases.
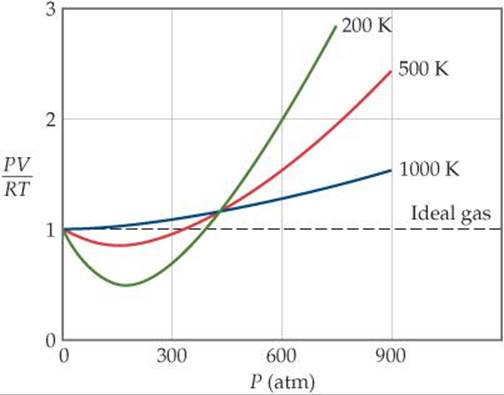
![]() FIGURE 10.23 The effect of temperature and pressure on the behavior of nitrogen gas.
FIGURE 10.23 The effect of temperature and pressure on the behavior of nitrogen gas.
Deviation from ideal behavior also depends on temperature. As temperature increases, the behavior of a real gas more nearly approaches that of the ideal gas (![]() FIGURE 10.23). In general, the deviation from ideal behavior increases as temperature decreases, becoming significant near the temperature at which the gas liquefies.
FIGURE 10.23). In general, the deviation from ideal behavior increases as temperature decreases, becoming significant near the temperature at which the gas liquefies.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
Under which conditions do you expect helium gas to deviate most from ideal behavior?
a. 100 K and 1 atm,
b. 100 K and 5 atm, or
c. 300 K and 2 atm.
The basic assumptions of the kinetic-molecular theory of gases give us insight into why real gases deviate from ideal behavior. The molecules of an ideal gas are assumed to occupy no space and have no attraction for one another. Real molecules, however, do have finite volumes and do attract one another. As ![]() FIGURE 10.24 shows, the unoccupied space in which real molecules can move is less than the container volume. At low pressures the combined volume of the gas molecules is negligible relative to the container volume. Thus, the unoccupied volume available to the molecules is essentially the container volume. At high pressures, the combined volume of the gas molecules is not negligible relative to the container volume. Now the unoccupied volume available to the molecules is less than the container volume. At high pressures, therefore, gas volumes tend to be slightly greater than those predicted by the ideal-gas equation.
FIGURE 10.24 shows, the unoccupied space in which real molecules can move is less than the container volume. At low pressures the combined volume of the gas molecules is negligible relative to the container volume. Thus, the unoccupied volume available to the molecules is essentially the container volume. At high pressures, the combined volume of the gas molecules is not negligible relative to the container volume. Now the unoccupied volume available to the molecules is less than the container volume. At high pressures, therefore, gas volumes tend to be slightly greater than those predicted by the ideal-gas equation.
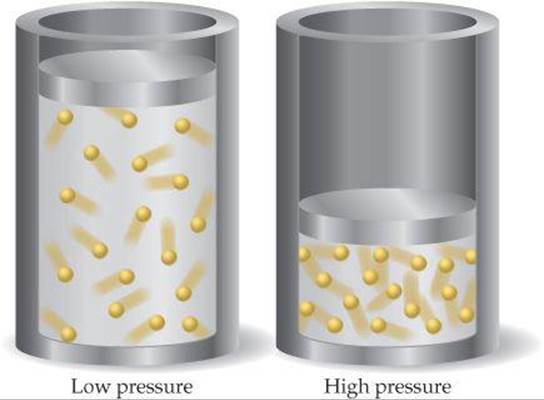
![]() FIGURE 10.24 Gases behave more ideally at low pressure than at high pressure. The combined volume of the molecules can be neglected at low pressure but not at high pressure.
FIGURE 10.24 Gases behave more ideally at low pressure than at high pressure. The combined volume of the molecules can be neglected at low pressure but not at high pressure.
Another reason for nonideal behavior at high pressures is that the attractive forces between molecules come into play at the short intermolecular distances found when molecules are crowded together at high pressures. Because of these attractive forces, the impact of a given molecule with the container wall is lessened. If we could stop the motion in a gas, as illustrated in ![]() FIGURE 10.25, we would see that a molecule about to collide with the wall experiences the attractive forces of nearby molecules. These attractions lessen the force with which the molecule hits the wall. As a result, the gas pressure is less than that of an ideal gas. This effect decreases PV/RT to below its ideal value, as seen at the lower pressures in Figures 10.22 and 10.23. When the pressure is sufficiently high, however, the volume effects dominate and PV/RT increases to above the ideal value.
FIGURE 10.25, we would see that a molecule about to collide with the wall experiences the attractive forces of nearby molecules. These attractions lessen the force with which the molecule hits the wall. As a result, the gas pressure is less than that of an ideal gas. This effect decreases PV/RT to below its ideal value, as seen at the lower pressures in Figures 10.22 and 10.23. When the pressure is sufficiently high, however, the volume effects dominate and PV/RT increases to above the ideal value.
![]() GO FIGURE
GO FIGURE
How would you expect the pressure of a gas to change if suddenly the intermolecular forces were repulsive rather than attractive?
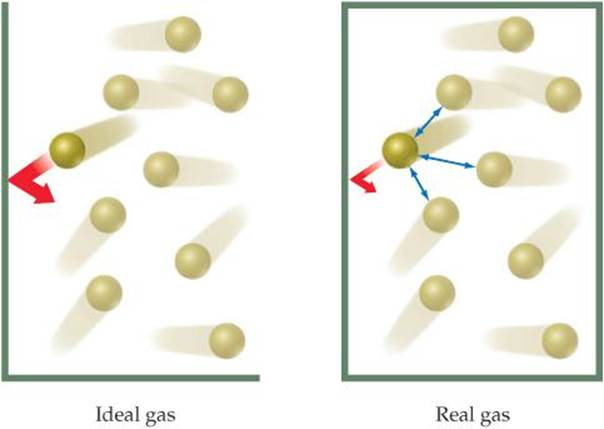
![]() FIGURE 10.25 In any real gas, attractive intermolecular forces reduce pressure to values lower than in an ideal gas.
FIGURE 10.25 In any real gas, attractive intermolecular forces reduce pressure to values lower than in an ideal gas.
Temperature determines how effective attractive forces between gas molecules are in causing deviations from ideal behavior at lower pressures. Figure 10.23 shows that, at pressures below about 400 atm, cooling increases the extent to which a gas deviates from ideal behavior. As the gas cools, the average kinetic energy of the molecules decreases. This drop in kinetic energy means the molecules do not have the energy needed to overcome intermolecular attraction, and the molecules will be more likely to stick to each other than bounce off each other.
As the temperature of a gas increases—as, say, from 200 K to 1000 K in Figure 10.23—the negative deviation of PV/RT from the ideal value of 1 disappears. As noted earlier, the deviations seen at high temperatures stem mainly from the effect of the finite volumes of the molecules.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
List two reasons why gases deviate from ideal behavior.
The van der Waals Equation
Engineers and scientists who work with gases at high pressures often cannot use the ideal-gas equation because departures from ideal behavior are too large. One useful equation developed to predict the behavior of real gases was proposed by the Dutch scientist Johannes van der Waals (1837–1923).
Van der Waals recognized that the ideal-gas equation could be corrected to account for the effects of intermolecular attractive forces and for molecular volumes. He introduced two constants for these corrections: a, a measure of how strongly the gas molecules attract one another, and b, a measure of the finite volume occupied by the molecules. His description of gas behavior is known as the van der Waals equation:
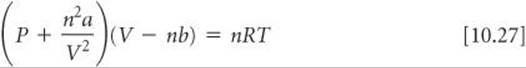
The term n2a/V2 accounts for the attractive forces. The equation adjusts the pressure upward by adding n2a/V2 because attractive forces between molecules tend to reduce the pressure (Figure 10.25). The added term has the form n2a/V2 because the attractive force between pairs of molecules increases as the square of the number of molecules per unit volume, (n/V)2.
TABLE 10.3 • Van der Waals Constants for Gas Molecules
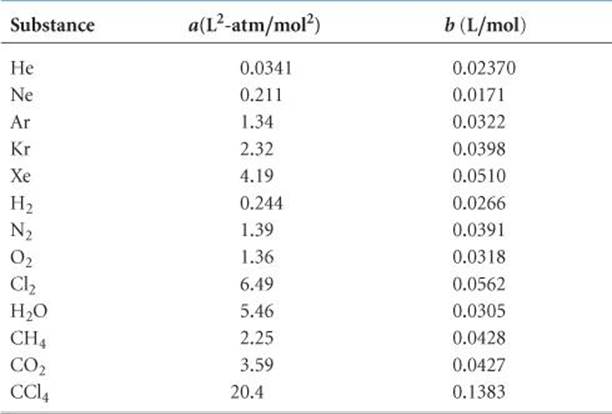
The term nb accounts for the small but finite volume occupied by the gas molecules (Figure 10.24). The van der Waals equation subtracts nb to adjust the volume downward to give the volume that would be available to the molecules in the ideal case. The constants a and b, called van der Waals constants, are experimentally determined, positive quantities that differ from one gas to another. Notice in ![]() TABLE 10.3 that a and b generally increase with increasing molecular mass. Larger, more massive molecules have larger volumes and tend to have greater intermolecular attractive forces.
TABLE 10.3 that a and b generally increase with increasing molecular mass. Larger, more massive molecules have larger volumes and tend to have greater intermolecular attractive forces.
SAMPLE EXERCISE 10.16 Using the van der Waals Equation
If 1.000 mol of an ideal gas were confined to 22.41 L at 0.0 °C, it would exert a pressure of 1.000 atm. Use the van der Waals equation and Table 10.3 to estimate the pressure exerted by 1.000 mol of Cl2(g) in 22.41 L at 0.0 °C.
SOLUTION
Analyze We need to determine a pressure. Because we will use the van der Waals equation, we must identify the appropriate values for the constants that appear there.
Plan Solving Equation 10.27 for P, we have
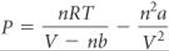
Solve Substituting n = 1.000 mol, R = 0.08206 L-atm/mol-K, T = 273.2 K, V = 22.41 L, a = 6.49 L2-atm/mol2, and b = 0.0562 L/mol:

Check We expect a pressure not far from 1.000 atm, which would be the value for an ideal gas, so our answer seems very reasonable.
Comment Notice that the term 1.003 atm is the pressure corrected for molecular volume. This value is higher than the ideal value, 1.000 atm, because the volume in which the molecules are free to move is smaller than the container volume, 22.41 L. Thus, the molecules collide more frequently with the container walls. The term 0.013 atm corrects for intermolecular forces. The intermolecular attractions between molecules reduce the pressure to 0.990 atm. We conclude, therefore, that the intermolecular attractions are the main cause of the slight deviation of Cl2(g) from ideal behavior under the stated experimental conditions.
PRACTICE EXERCISE
A sample of 1.000 mol of CO2(g) is confined to a 3.000-L container at 0.000 °C. Calculate the pressure of the gas using (a) the ideal-gas equation and (b) the van der Waals equation.
Answers: (a) 7.47 atm, (b) 7.18 atm
SAMPLE INTEGRATIVE EXERCISE Putting Concepts Together
Cyanogen, a highly toxic gas, is 46.2% C and 53.8% N by mass. At 25 °C and 751 torr, 1.05 g of cyanogen occupies 0.500 L. (a) What is the molecular formula of cyanogen? Predict (b) its molecular structure and (c) its polarity.
SOLUTION
Analyze We need to determine the molecular formula of a gas from elemental analysis data and data on its properties. Then we need to predict the structure of the molecule and from that, its polarity.
(a) Plan We can use the percentage composition of the compound to calculate its empirical formula. ![]() (Section 3.5) Then we can determine the molecular formula by comparing the mass of the empirical formula with the molar mass.
(Section 3.5) Then we can determine the molecular formula by comparing the mass of the empirical formula with the molar mass. ![]() (Section 3.5)
(Section 3.5)
Solve To determine the empirical formula, we assume we have a 100-g sample and calculate the number of moles of each element in the sample:
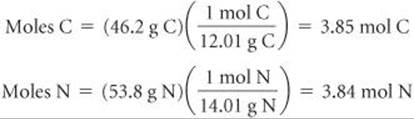
Because the ratio of the moles of the two elements is essentially 1:1, the empirical formula is CN. To determine the molar mass, we use Equation 10.11.

The molar mass associated with the empirical formula CN is 12.0 + 14.0 = 26.0 g/mol. Dividing the molar mass by that of its empirical formula gives (52.0 g/mol)/(26.0 g/mol) = 2.00. Thus, the molecule has twice as many atoms of each element as the empirical formula, giving the molecular formula C2N2.
(b) Plan To determine the molecular structure, we must determine the Lewis structure. ![]() (Section 8.5) We can then use the VSEPR model to predict the structure.
(Section 8.5) We can then use the VSEPR model to predict the structure. ![]() (Section 9.2)
(Section 9.2)
Solve The molecule has 2(4) + 2(5) = 18 valence-shell electrons. By trial and error, we seek a Lewis structure with 18 valence electrons in which each atom has an octet and the formal charges are as low as possible. The structure
![]()
meets these criteria. (This structure has zero formal charge on each atom.)
The Lewis structure shows that each atom has two electron domains. (Each nitrogen has a nonbonding pair of electrons and a triple bond, whereas each carbon has a triple bond and a single bond.) Thus, the electron-domain geometry around each atom is linear, causing the overall molecule to be linear.
(c) Plan To determine the polarity of the molecule, we must examine the polarity of the individual bonds and the overall geometry of the molecule.
Solve Because the molecule is linear, we expect the two dipoles created by the polarity in the carbon–nitrogen bond to cancel each other, leaving the molecule with no dipole moment.