CHEMICAL BIOLOGY
Receptor-Ligand Interactions in Biological Systems
Liwei Li, Department of Biochemistry and Molecular Biology and the Center for Computational Biology and Bioinformatics, Indiana University, Indianapolis, Indiana
Samy O. Meroueh, Department of Biochemistry and Molecular Biology, Center for Computational Biology and Bioinformatics, and the Department of Chemistry and Chemical Biology, Indiana University Purdue University, Indianapolis, Indiana
doi: 10.1002/9780470048672.wecb506
Despite the significant research that has been invested in understanding molecular recognition in biological systems, accurate prediction of macroscopic properties based on microscopic interactions remains elusive, which makes it difficult to identify systematically tight binding inhibitors in computational drug design. In the past, most ligand design efforts have centered on descriptors derived mainly from structure, neglecting entropic effects that develop from receptor flexibility. The lack of explicit incorporation of receptor motion has meant that compensatory effects between enthalpy and entropy, which are essential for the accurate estimation of free energy, have also been neglected. In addition, cooperative effects, which develop from alteration in the motion of the receptor because of ligand binding, are not captured. These effects pose a challenge for the design of small molecules that allosterically modulate protein-protein and protein-small-molecule interactions. Here, we describe macroscopic properties of receptor-ligand interactions, which are followed by a discussion of how these properties are predicted with microscopic interactions. A discussion then ensues on some fundamental aspects of the molecular recognition process that have attracted renewed attention, such as conformational selection versus induced-fit binding, entropy-enthalpy compensation, and allostery.
Introduction
Molecular recognition leads to the association of macromolecules, which enables them to perform functions that are vital to the survival of an organism. Evolutionary forces have exploited interactions between macromolecules for the purpose of performing one of a multitude of tasks, including chemical modification (1), transportation (2), signal transduction (3), or recruitment of other macromolecules (4), among other things. The recognition process is driven by a balance between potential energy that develops from physical interactions at the molecular level (5) and kinetic energy that originates from inherent dynamics contained in molecules (6). The physical interaction between macromolecules is driven by various interactions most prominent among them electrostatics, which develops from the positive and negative charge of nuclei and electrons (6) and the hydrophobic effect (7-11). These charges impart attractive and repulsive characteristics to molecules. But it is often overlooked that the dynamics of molecules also play an important role in the recognition process (6)
In solution, molecules constantly encounter each other through collisions. At close distances, repulsions from the nuclei dominate. The balance between repulsive and attractive forces often lead to an equilibrium state such that two molecules will remain associated in a complex. In this state, dispersion or London forces dominate. The motion experienced by the molecules also plays a crucial role in this process. A molecule contains translational, rotational, as well as internal vibrational motion. When two molecules associate, conservation of energy dictates that the energy that is initially contained in translation and rotation must be eventually absorbed internally by the molecules through vibrations (12). The failure to effectively absorb this energy could lead in turn to the disruption of the balance between attractive and repulsive forces and the abrogation of the complex.
Although interactions between macromolecules and their ligands are normal processes essential to the survival of an organism, it is often the case that these same interactions will contribute to pathological processes. Examples include the binding of a growth factor to its cell surface receptor (3, 13), a matrix-metalloproteinase binding to its ligand (14), or the binding of a kinase to its ATP substrate (15). Each of these interactions has been targeted by pharmaceutical companies for the development of drugs. Inhibition of the receptor tyrosine kinases has been particularly successful. Targeting the abl kinase, for example, has led to the discovery of Gleevec (Novartis, East Hanover, NJ), which is one of the most effective anticancer therapeutics to date (16). This drug was rationally designed such that structural information of its target was used during the drug-discovery process. It is likely that early version of the drug underwent a series of chemical modifications to optimize not only affinity to the target but also ADME (adsorption, distribution, metabolism, and excretion), toxicology, and pharmacokinetic properties (17). But high affinity to the drug target remains a key criterion that must be constantly maintained. In addition, with the multitude of targets that are now available, selective or broad-spectrum inhibitors are also desirable. Despite the significant progress that we have made over the past decade toward understanding molecular recognition, the systematic ability to design molecules with high affinity to a target based on its structure remains elusive (18).
The focus of this review article will be on the interaction between macromolecules and small-molecule ligands. The discussion will first center on the thermodynamic and kinetic characteristics that are used to measure the extent of binding. Subsequently, we discuss the interactions at the atomic level that drive complex formation. Then, a discussion follows of some tools available to predict macroscopic properties from microscopic properties. We then briefly discuss macromolecular motions as well as various aspects of receptor-ligand that have attracted renewed attention, such as conformational selection versus induced-fit, enthalpy-entropy compensation effect, and protein allostery.
Macroscopic Properties
In solution, the mixing of two entities leads to the formation of a chemical equilibrium that is represented by the following equation:
![]()
where M is the macromolecular receptor, L is the small molecule ligand, and ML represents the complex between the receptor and ligand. Depending on the strength of the interaction, the equilibrium can favor the formation of reactants or products. The direction of the equilibrium is measured by a ratio known as the equilibrium constant, which is also known as either the dissociation constant KD or the association constant KA defined as follows:
![]()
A measure of the spontaneity of the chemical event is encapsulated in the Gibbs free energy, which is related to the equilibrium constant following this relation:
![]()
∆G is the free-energy change, ∆C° is standard free-energy change, R is the gas constant whose value is 8.31 J mol-1 K-1, and T is the temperature.
A chemical event that results in a reduction of the free energy is referred to as exergonic, whereas a process that results in an increase in the free energy is known as endergonic. Typical values of dissociation constants KD for receptor-ligand interactions occur between 10-3 (millimolar) and 10-9 (nanomolar) (19-21), although reports suggest values that reach the picomolar regime (19-21). Each order of magnitude in KD corresponds to a change in the free energy ∆G° of 1.4 kcal/mol-1. Hence, AG° for a millimolar ligand is —4.2 kcal/mol, whereas that of a nanomolar ligand is —9.8 kcal/mol. Another well-known equation relates the free energy to the enthalpy (∆H°) and entropy (∆S°):
![]()
The enthalpy is defined by the following expression:
![]()
where E is the internal energy of the system, P is the pressure, and V is the volume. Most chemical events occur at constant volume and pressure, and hence the enthalpy can be conceptualized as a measure in the internal energy change. The formation of favorable interactions, such as hydrogen bonds or van der Waals contacts will result in a negative enthalpy change and hence an exothermic process. The loss of favorable interactions leads to a positive enthalpy or endothermic process.
Although the enthalpy is a measure of order in the system, the entropy is a measure of disorder. The second law of thermodynamics states that a spontaneous event results in an increase in entropy. Hence, a favorable process always results in an increase in disorder. The entropy is defined as:
![]()
where S is the entropy and Ω is the phase space that corresponds to all the possible states that a system may adopt. In Newtonian mechanics, a state can be defined by position and velocity. In macromolecules, position can be translated into internal coordinates, such as bonds and torsions that define the conformation of the macromolecule. In the context of receptor-ligand binding, the change in the entropy is the log of the ratio of phase space of the receptor — ligand complex and the phase space of the product of the receptor and ligand. The number of states that are accessible for the free receptor and ligands will be significantly larger than that of the complex. Hence, the association of macromolecules and their ligands typically results in entropy loss (22). In some instances that involve the burial of hydrophobic residues, the rearrangement of water could lead to a favorable contribution from entropy (vide infra).
Microscopic Interactions
Molecules can have a net positive defined as negative charge depending on the hybridization state of atoms within them. In solution, the net charge often originates from ionizable groups that act as a Bronsted base or acid following this equation:
![]()
Carboxylate, thiols, or amino moities are a few examples of ionizable groups at physiological pH. The propensity of an ionizable group to lose a proton is measured by the pKa, which is defined by the following:
![]()
where Ka is the acid dissociation constant, [A-] and [HA] are the concentrations of acid and its conjugate base. Based on this equation, the pKa can also be viewed as the pH at which the concentration of base is equal to that of the acid. For example, at neutral pH, the pKa of the amino group of a lysine residue is 10.4, whereas that of a glutamic acid residue is 4.5 [pKa values are from Refs. 23 and 24]. In the former, the amino group is protonated and positively charged at physiological pH, whereas the glutamic acid is unprotonated and negatively charged. Other examples of amino acids with positively charged side chains include the guanidine side chain of arginine (pKa = 12.5). Another example of an amino acid with a negatively charged group include aspartic acid (pKa = 4.0).
Within macromolecules, however, the pKa of ionizable groups can deviate from their standard values, as the groups are not only surrounded by solvent but also by other residues. For example, a carboxylic acid moiety located in a region of low polarity or hydrophobicity will experience an increase in its pKa. A positive charge near the carboxyl group will reduce its pKa, whereas a negative charge will lead to a more basic side chain. Conversely, an amino group in a hydrophobic region will experience a reduction in its pKa, whereas a salt bridge will increase its pKa. A prominent example that illustrates these trends occurs in the TEM-1 β-lactamase, which is a resistance enzyme in bacteria that destroys β-lactam antibiotics (25). The active site contains two lysine residues and two serine residues in a cross-like arrangement (Fig. 1). This arrangement is universally conserved not only among the β-lactamases but also among their ancestors, the penicillin-binding proteins (PBPs) (26). A lysine residue that is essential for catalysis is found in a hydrophobic pocket that is shielded from direct contact with solvent (Fig. 1). A nearby glutamate side chain (Glu-166) forms a salt-bridge interaction with Lys-73. Biochemical analyses had ascribed a pKa of 5 to Glu-166, nearly 0.5 units higher than that of standard pKa of 4.5. An extensive set of biochemical, nuclear magnetic resonance (NMR), and molecular dynamics-based free-energy calculations led to a pKa value of 8 for Lys73, which is nearly 2.8 units lower than its standard pKa. These pKa shifts can be rationalized from the microenviroment around the residues. The reduced pKa of Lys73 is promoted by the low dielectric medium that surrounds its amino group along with the positive charge of a nearby lysine (Lys234). The negative charge that emanates from Glu166, on the other hand, stabilizes the positive charge on Lys73 and thus raises its pKa. Interestingly, in the PBPs, which lack a glutamate in its active site (27), the pKa of the catalytic lysine residue is reduced even more to 6, such that the amino group on the lysine side chain is neutral (25). The neutrality of the side chain is essential for this enzyme to carry out its transpeptidase function (27).

Figure 1. A stereoview image that depicts the active site of TEM-1 β-lactamase from E. coli. The protein is depicted in capped-sticks representation. Residues are shown in capped-sticks representation and color-coded according to atom types (N, C, O, and H in blue, white, red and cyan, respectively). The red arrow points to Lys-73, and the white arrow points to Glu-166.
Electrostatic interactions, along with hydrophobic effects, form the basis of most intermolecular forces that drive receptorligand interactions in biological systems. The simplest form of electrostatic interaction is the salt bridge, which occurs between two oppositely charged functional groups (28). The formation of such an interaction within proteins is usually energetically costly (29). An example is the Lys73 and Glu166 salt bridge that was alluded to above (Fig. 1). Other examples of charge-charge interactions in biological molecules include the coordination of transition metals with negatively charged moieties such as carboxylates from glutamate and aspartate side chains or thiolates from cysteine residues (30, 31). Although opposite charges form strong interactions, their presence alters the charge distribution of surrounding residues as well. A fixed charge creates an electric field that emanates from it (for a positive charge). Electrons on surrounding atoms will be polarized depending on the nature of the field. For a positive charge, the electron density on surrounding atoms will move toward the charge, whereas a negative charge will cause electrons to move away. This movement of electron density creates a dipole. The region where the electron density is accumulating will be negatively charged, whereas the region that lost electron density will develop a partial positive site. Some dipoles are permanent (32). A prominent example is that of water, in which the electrons accumulate on the electronegative oxygen atom, leaving a partial positive charge on the hydrogen atoms and a permanent dipole that can be visualized as a vector that is perpendicular to the base of the HOH triangle (33). It is worth mentioning that the interaction energy between a charge and a dipole is inversely proportional to their separation to the fourth power, whereas a dipole-dipole interaction is inversely proportional to the separation to the sixth power. Hence, these interactions dominate at short separations, whereas charge-charge interactions dominate at large separations.
A ubiquitous interaction that is electrostatic in nature and commonly occurs in biological systems is the hydrogen bond (see Fig. 1 for examples). It is defined as the interaction between an electronegative atom (acceptor) and a hydrogen atom that is covalently attached to another electronegative atom (donor) (34, 35). At the fundamental level, a hydrogen bond has been described as a dipole-dipole interaction, but it is likely more complex mixture of physical effects that include covalent characteristics, polarization, as well as charge transfer (34-37). A common hydrogen bond in proteins occurs between an NH bond and an oxygen atom from a carbonyl carbon with an NO distance that falls between 2.8 and 3 A, and between 1.5 and 2 A for the OH distance. A recent series of surveys conducted on protein-ligand complexes from the Repository Collaboratory of Structural Bioinformatics find that the strongest hydrogen bonds occur for the NH-O (ligand is donor and backbone is acceptor), NH-O (side chain is donor and ligand is acceptor), OH-O (ligand donor and backbone is acceptor), and OH-O (side chain donor and ligand acceptor) bonds with donor-hydrogen-acceptor angles near linearity (38). The textbook definition of the hydrogen bond mentions only N, O, S as donors, but recent work has suggested that carbon can also act as donor atom in the formation of weaker CH-X hydrogen bonds (39, 40), where X = O, N. A comprehensive database analysis suggested that CH-O hydrogen bonds occurred extensively in alpha helices (41). Solvent tends to weaken the CH-O hydrogen bond (42). Other atoms, such as halogens, have been suggested to act as a bridge between a hydrogen bond donor and acceptor (43)
In addition to promoting more favorable intermolecular interactions between receptor and ligand, electrostatic interactions play an important role in the interaction between water and solutes. Water molecules have the tendency to form ordered structures, although it is worth mentioning that the extent of ordering has been difficult to determine (44). Hydrocarbons have a tendency to favor water ordering at 25 °C and are hence immiscible in water (45). This effect is also observed around nonpolar surfaces of macromolecules in which water molecules are more ordered that in bulk water, resulting in an entropic penalty (46). This effect is known as the hydrophobic effect and is caused by the special hydrogen bonding properties of water (7-11). A key signature of the hydrophobic effect is a change in the heat capacity (47). It is widely accepted that this effect plays an essential role in protein folding, as hydrophobic residues tend to aggregate at the core of folded proteins whereas hydrophilic moieties are found on the exterior of proteins, maximizing contact with the water solvent (47). In the context of protein-ligand interactions, the hydrophobic effect is defined as the additional stability that is gained as a result of binding in water, specifically caused by the removal of nonpolar surfaces from exposure to water during complex formation. In the case of a small-molecule ligand, the burial of nonpolar functional groups into a protein cavity will be favorable, especially when the cavity is also hydrophobic in nature; here, the hydrophobic effect can exhibit a favorable enthalpic component (48). The magnitude of the hydrophobic effect is proportional to the amount of surface buried as a result of binding.
Predicting Macroscopic Properties From Microscopic Interactions
The 1990s experienced a surge in the number of X-ray and NMR structures that were solved for macromolecules and their complexes. This surge coincided with 1) a rapid increase in computer power and 2) an increase in the availability of computational chemistry programs that could perform molecular dynamics simulations as well as quantum chemical calculations on systems of biological relevance (49, 50). These changes emboldened scientists to apply computational techniques to biological systems that were otherwise not previously amenable to accurate calculations. Early attempts were mostly limited at predicting the binding mode of compounds, which is a process known as docking. One of the first computer programs to perform docking was DOCK, written by Erwin Kuntz and coworkers at the University of California San Francisco (51). The process of docking consists of sampling many conformations of the ligand bound to the receptor until the most energetically favorable complex is found (52). Today programs perform docking with both ligand and receptor flexibility (53), including GOLD (54), AutoDock (55), and FlexX (56). The main impediment with docking, however, has been that the accuracy of scoring function that is used to treat the interaction between ligand and receptor (57). Scoring functions were devised with the purpose of estimating the binding free energy of a molecule to its receptor. Several techniques have been used, which include empirical (58-60), knowledge-based (61-64), or physics-based methods (51, 65-67). But insufficient sampling of conformational space (docking typically is conducted on a single snapshot, with at most local flexibility), as well as the lack of accuracy in the force fields used to represent the interaction between compound and receptor, have hampered efforts at obtaining more accurate approximation of the free energy of binding (68).

Figure 2. Stereoview that illustrates the motion that is experienced by a protein-ligand complex during molecular dynamics simulation.
Scoring functions were devised as an alternative to highly intensive methods for computing the free-energy binding. The compute-intensive methods are typically based on molecular dynamics simulations (MD), which consist of solving Newton’s equations of motion to determine the position and velocities of atoms with respect to time (69). With these simulations, one can gain detailed insight into the dynamics of the system, which can be used to estimate entropy of binding (Fig. 2) (70). Several packages have facilitated the process of carrying out MD simulations for biological systems; these methods include AMBER (71), CHARMM (72), and GROMACS (54, 73) among others. Two requirements exist for conducting an MD simulation, namely a three-dimensional structure, initial velocities for all atoms in the system, and the potential energy of the system (69). The structure is usually obtained from x-ray or NMR. The velocities can easily be obtained from the temperature. The potential energy is obtained through what is known as a force field, which is a mathematical representation of the energy of the system (68). A typical force field contains terms to represent bonds, bends, torsions, and intermolecular interactions in a system, and it takes the following form:
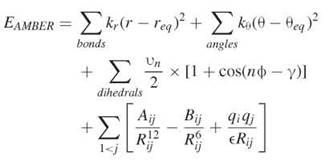
here, EAMBER is the potential energy, req and θeq are equilibrium distance and angles for bonds and bends, respectively, and Kr, Kθ, vn are force constants; n is multiplicity and γ is the phase angle for the torsional angle parameters. The accuracy of force fields remains the main impediment for the accurate computation of free energies based on molecular dynamics simulations (68).
Several methods based on molecular dynamics simulations have been devised to compute the free energy of binding (22, 74), including free-energy perturbation (FEP) and thermodynamic integration (TI). These methods are most useful for estimating the free-energy change as a result of the substitution of a functional group into another [e.g., the conversion of a hydrogen atom (initial state) to a methyl group (final state) (75). In practice, these techniques consist of running multiple simulations at different values of a coupling parameter that ranges from 0 to 1. Depending on the substitution that is being made, the coupling parameter is multiplied to the relevant terms in the force field such that the initial state gradually converts to the final state. We have recently applied the thermodynamic integration approach toward estimating the pKa of a residue in the class A β-lactamase (25) and the penicillin-binding proteins with remarkable success (76). The deprotonation reaction constitutes the full thermodynamic cycle for free-energy variations in aqueous condition, which forms the basis for Eqs. (1-3), and was used to calculate the pKa of the lysine residue:

where AH+ corresponds to the protonated Lys73 and BH+ is for the protonated Lys306 (see Fig. 1). The pKa value of Lys306 is expected to be that of a typical lysine (because it is a surface residue). The following equation was used to compute the pKa:
![]()
where ∆G = ∆∆Gaq(A—AH+)-∆∆Gaq(B—BH+) (inkcal ∙ mol-1). The constant 0.729 is the value of 1/(2.303 RT) with gas constant R = 1.984 x 10—3 kcal ∙ K—1 ∙ mol-1 and temperature T = 300 K, and pKa(BH+) = 10.8 for the unperturbed surface lysine in the aqueous milieu. ∆∆Gaq (X—XH+) was computed using the thermodynamic integration approach, which is the free-energy difference between the unprotonated state X and protonated state XH+,
![]()
With the thermodynamic integration method the difference is evaluated with a 12-point Gaussian quadrature,
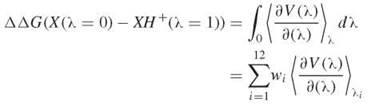
where wi and λi are known (77).
However, when it comes to computing the free-energy difference between two very different molecules, FEP or TI are not suitable (78). Other techniques have been devised for that purpose, such the MM-PBSA (79, 80) and LIE (81) methods. The MM-PBSA approach is based on the following thermodynamic cycle:
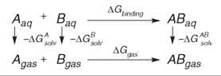
The free-energy change ∆Gbinding is thus expressed by the following equation:
![]()
In practice, the method consists of running a molecular dynamics simulation of the receptor ligand complex, then collecting a series of snapshots, which is followed by energy calculation, solvation energy calculation, and entropy calculation for complex, receptor, and ligand. We have applied this method to protein-ligand as well as nuclei-acid — ligand interactions in the past. The method seems to perform best in calculations of differences in free energy (82), but sometimes it performs well for absolute value calculations of the free energy (83, 84).
Receptor Flexibility in Computational Design
In solution, macromolecules are not static as suggested by structural characterization, but instead they experience a range of inherent motions that are essential to their functions (85, 86). These motions that are characterized by large scale conformational changes that occur on the micro to millisecond time scale (87, 88). Examples include an open to closed conformation sampled by an enzyme during catalysis (89), or the conformational transitions that are observed in SecA helicase-like motor that couples ATP hydrolysis to the translocation of extracytoplasmic protein substrates (90). But while experiencing these large-scale transitions, macromolecules are not static; they undergo constant atomic fluctuations that occur on the picoseconds to nanosecond regime (91, 92). Recently, it was shown that shorter and longer time scale motions can both influence macromolecular function such as catalysis (88). It was found that shorter timescale atomic fluctuations in hinge regions of adenylate kinase facilitate the large-scale slower lid motions that produce a catalytically competent state.
Incorporation of receptor flexibility is particularly relevant in computational drug design. Several efforts in the past have attempted to incorporate flexibility into the drug design process using normal mode analyses (70), phamacophore concept coupled with molecular dynamics simulations (93) and essential dynamics derived from molecular dynamics simulations. More recently, a knowledge-based function was derived to incorporate receptor flexibility (94). Other methods have focused on the local environment of the ligand binding site by strictly considering side-chain motion surrounding the ligand (95). It is often the case that ligand binding will lead to significant alteration in structure that may not be sampled by standard techniques. Recently, a new approach was developed to consider these conformational changes (96)
Induced-Fit Versus Conformational Selection
More than 100 years ago, Emil Fisher had proposed the lock-and-key hypothesis to explain how an enzyme associates with its substrate (97). He proposed that the substrate (key) adopts a shape that is highly complementary to the receptor (lock), which suggests that an enzyme was predisposed to bind to its substrate. But crystal structures of macromolecules in their apo and liganded states have shown that significant conformational changes can often occur during complex formation (98-100). An update of the lock-and-key model, which is known as the induced-fit hypothesis, was later put forward by Koshland (101). It assumes that the enzyme or macromolecule does not sample complementary structures to the ligand, and hence the necessary conformational changes required for complex formation are caused directly by the ligand on binding. An alternative to the induced-fit model has been proposed in light of a growing body of data suggesting that proteins are inherently highly dynamic and hence sample many conformational states (90, 102-104). This model is often referred to as the pre-existing equilibrium or conformational selection model as an alternative to the induced-fit model. It is closely related to the Monod-Wyman-Changeux (MWC) model, which was introduced more than four decades ago to describe allostery in hemoglobin (105). They proposed that a protein exists in an ensemble of conformational states that co-exist in equilibrium; the ligand will bind to one of these conformations and shift the equilibrium toward complex formation. Several authors have discussed these matters extensively, including Hecht et al. (106) and Miller and Dill (107). A prominent example in support of conformational selection was highlighted more than a decade ago by Foote and Milstein (108). Using stopped-flow fluorescence experiments, they found that antibodies existed at an equilibrium between different conformers, with ligands binding preferentially to one form. More recently, James et al. (109) employed X-ray crystallography and pre-steady-state kinetics to propose that antibodies adopt multiple conformers and thereby bind unrelated antigens. But they also suggest the possibility of induced fit on association of receptor and ligand. The conformational selection model was recently supported with computation using normal mode analyses (110)
We recently studied conformational change caused by ligand binding in the bacterial ribosome acyltransfer site (A site), where antibiotics are known to lead to mistranslation and the eventual demise of the organism (111). The conformational change was discovered after the elucidation of the three-dimensional crystal structure of the 30S ribosome (112). It entails the flipping of two bases A1492 and A1493 from an intrahelical stacked conformation to an extrahelical conformation that is completely solvent exposed. We have recently conducted extensive explicit-solvent molecular dynamics simulation to study the base-flipping event (Fig. 3) (113). We found that in the absence of the aminoglycoside antibiotic, the flipping event has a large barrier of nearly 20kcal/mol, but the overall process remains thermodynamically favorable (exergonic). However, in the presence of the antibiotic we discovered that the barrier for base flipping was significantly reduced, and the overall process also remained exergonic. The flipping seemed to be mostly favored by entropic and electrostatic components of the free energy. These results suggest that in the absence of antibiotic, the base flipping occurs continuously supporting a conformational selection model for codon-anticodon recognition process. In the presence of the ligand, however, it was clear that the flipping was induced by the ligand and hence suggests an induced-fit mechanism. It is very likely that molecular recognition likely involves a mixture of conformational selection and induced fit.
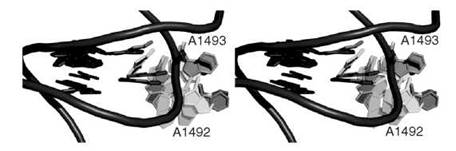
Figure 3. A stereoview close-up of the acyltransfer site of the 30 S ribosome revealing the based flipping event that is experimented by A1492 and A1493 during a molecular dynamics simulation (see Reference 70). RNA backbone is shown in purple tube representation whereas bases are shown in capped sticks rendering.
Enthalpy-Entropy Compensation (EEC)
It has been known for several decades that the formation of complexes between molecules through weak interactions results in a change of the enthalpy that is accompanied by an opposite change in the entropy (114-116). This effect, which is known as enthalpy-entropy compensation (EEC) (117), can be a hindrance in drug-design efforts. For example, a recent effort at optimizing a picomolar HIV-1 inhibitor based on the crystal structure of the inhibitor bound to the active site resulted in a compound with similar binding affinity (118). The addition consisted of replacing a thioester group by a sulfonyl group. The original compound had ∆H = —8.2 kcal/mol and —T∆S = —6.7 kcal/mol. The optimized compound showed a gain in enthalpy by 3.9 kcal/mol, which signifies that more favorable interactions were created. However, an equal and opposite compensation of the entropy resulted, leading to no gain of free energy.
Our recent work on the study of binding of the antibiotic vancomycin to bacterial cell wall with isothermal titration calorimetry also illustrated the effect of entropy enthalpy compensation (119). The backbone of the cell wall is made up of alternating N-acetylglucosamine (NAG) and N-acetylmuramic acid (NAM). The NAM residues are incorporated with a pentapeptidyl stem, which terminates in acyl-D-Ala-D-Ala. The study found that the binding of vancomycin to the acyl-D-Ala-D-Ala fragment resulted in the same free-energy change as the second vancomycin binding to cell wall fragment with two NAG-NAM units. Despite the similarity in the binding affinity, the entropy and enthalpy contributions for binding to the cell wall fragment were different, and the 5 kJ/mol gain in enthalpy was compensated by a loss of 5 kJ/mol in entropy (119)
It has been argued that EEC is a mere artifact (120). In an attempt to establish the existence of the EEC effect, a collection of thermodynamic data collected for the binding of 136 drugs to their receptors revealed strong correlation between enthalpy and entropy (116). Some have attributed these results to inaccuracies of the van’t Hoff analysis that is used for the measurement of thermodynamic parameters (121). But isothermal titration calorimetry data (ITC) does not suffer from the same inaccuracies that plague the van’t Hoff analysis. We have recently created a dataset that contains more than 400 entries containing structural and isothermal titration data (122). A plot of the enthalpy and entropy results in the following linear relationship:
![]()
Analysis of the data from our dataset has firmly established the existence of the EEC effect (122).
Nearly a decade ago, Dunitz et al. (114) attempted to rationalize the EEC effect with the use of statistical thermodynamic concepts. Using a model for two covalently attached atoms whose bond is described with a Morse potential, he showed that the vibrational entropy decreased exponentially with the frequency of vibration of the bond. In the context of macromolecules, this signifies that the high frequency motions such as bond stretching and bending that occur with frequency greater than 1000 cm-1 contribute little to the entropy, whereas lower frequency motions, such as those that involve entire domains, make the largest contribution. Using a hypothetical model of a water molecule bound to a macromolecule with a dissociation enthalpy of 5 kcal/mol, the author estimated an entropic contribution of 4.5 kcal/mol, nearly completely balancing the enthalpy. A plot of the vibrational entropy versus the dissociation enthalpy revealed that for weak interactions (less than 5 kcal/mol), the contributions of enthalpy and entropy compensated each other. These results support earlier plots by Searle et al. (115) that revealed a similar effect from a curve derived based on qualitative thermodynamic considerations. It is of interest to note that the plot of entropy versus enthalpy monotonically increased with respect to enthalpy, which is likely caused by the neglect of the role of solvation in the model (release of water molecules generate favorable entropy that should dampen the steep enthalpy increase). These early theoretical treatments of EEC have been followed by more recent work by Ford (123) who argues that in the gas phase, EEC is not a general feature of association. He bases this argument on the observation that both compensation and anticompensation (negative correlation between AH and AS) develop from this model. Other investigators have derived a theoretical treatment (117) that supports the EEC effect, but only within a 20% range of the experimental temperature Tc = d AH/d AS. Other notable investigators that have extensively dealt with the issue of enthalpy-entropy compensation, including Sharp (117), Cooper (124), and Jen-Jacobsen et al. (125)
Allostery
In 1967, it was discovered that the binding of oxygen to one of the monomers of the hemoglobin tetramer led to a change in the affinity of oxygen on the other subunits of hemoglobin, despite the large distances that separate the oxygen binding sites (126). This effect, which is now known as allostery, has been since observed in a multitude of systems (127, 128). In general, a triggering event at one site of a macromolecule or macromolecular complex leads to an effect at a distal site. The triggering event could be caused by binding of a ligand, or a macromolecule. But it could also be caused by a chemical reaction. The resulting effect that occurs at a distal site could range from modulation of the binding affinity of a ligand (103, 129, 130), to alteration of catalysis (131-133), to causing significant conformational change that is usually essential for the function of the protein (134-136). An extensive list of structures of allosteric system in their initial and final states has been recently compiled (137)
Just as in ligand binding, allostery can be discussed in terms of the conformational selection and induced-fit mechanisms. The difference is that the triggering event would be causing an effect at a distal site. In the context of conformational selection, the ligand will select not only those conformers that facilitate its binding but also those that lead to an effect at the distal site. If the effect is an enhancement of catalysis, then the ligand would be selecting those conformers with residues at the distal site that are positioned such that the transition state free-energy barrier for reaction would be reduced. If, on the other hand, the effect is enhancement of binding, then the ligand would be selecting conformers that are both suitable for its binding as well as suitable for the binding of another ligand at a distal site.
Induced fit in allostery would entail a propagation of conformational changes from the triggering site to the distal site. This idea was initially proposed to explain cooperativity in hemoglobin by Perutz et al. (138, 139) who suggested a set of consecutive conformational changes that lead hemoglobin from its T-state (tense) to its R-state (relaxed). More recently, Pettigrew and co-workers (140, 141) have proposed the existence of a coupling pathway between two distal sites to explain how glycerol kinase from Escherichia coli but not Hemophilus influenza is inhibited allosterically by phosphotransferatse system protein IIAGlc. Through specific mutations, they could interconvert these systems, which confirms the existence of a pathway and suggests that allostery was an evolutionary effect. Another example where specific paths are believed to connect distal sites is the tRNA synthase system. Cognate recognition between anticodon on aa-tRNA and the codon on mRNA signals tRNA synthase to perform its function at a catalytic site that is located more than 70 A away (142). Although most studies have invoked structural change as the main conduit between distal sites, evidence has been mounting that in addition to structural changes, molecular motion, both in the short (103) and longer (102, 103, 132, 143) timescales, plays an important role in allostery.
A prominent allosteric system in which ligand binding at one site causes a change in the affinity of another ligand at another site is the catabolite activator protein or CAP (Fig. 4). In solution, the 47-kDa dimer exists as a homodimer and exhibits homotropic negative cooperativity, whereby the binding of the first cAMP molecule reduces the affinity of the second cAMP by nearly two orders of magnitude (144-146). The distance between the cAMP binding pockets on the two monomers is 24 A and precludes any contribution from electrostatic interactions. A recent NMR study has suggested that the anticooperative effect could be caused by changes in the dynamics of the system, rather than by structural changes (103). The NMR data show that the binding of the first ligand causes significant increase in the slower motions but a slight tightening of the faster motions, which is evidenced by a slight increase of the order parameter S2. Hydrogen/deuterium (H/D) exchange experiments show no overall change in the conformational change experienced by the system. The binding of the second ligand, however, causes significant tightening of the structure, both in the ps-ns and the μs-ms regime (103). The negative cooperativity is attributed to this loss of motion. In addition, significant stability of the structure is detected from lower H/D exchange rates.
We have conducted a thorough computational study of allostery in CAP to unravel the structural and dynamic changes that occur as a result of cAMP binding (132). Our extensive simulations for the apo, singly liganded, and doubly liganded CAP have confirmed results obtained from NMR (103), namely that cAMP binding to one monomer causes changes both in the shorter and longer timescale motions. The shorter timescale motions were measured by computing the order parameter S2, whereas the longer timescale motions were obtained through a principal component analysis of the dynamics trajectory. Our simulations, however, included the DNA-binding domain that was absent in the NMR studies. We observed a remarkable conformational change that entailed the complete separation of the ligand binding and DNA-binding domains (Fig. 4). The unique aspect of this conformational change was that it only occurred in unoccupied monomers (Fig. 4). Hence it seems that ligand binding causes significant stabilization of the ligand-binding domain. When our calculations were repeated in the presence of DNA, however, we found that a switch in the cooperativity occurred, whereby the binding of the second cAMP was significantly favored by several kcal/mol (132). This finding explained the seemingly contradictory fact that CAP has evolved to disfavor the binding of another cAMP, but that doubly liganded CAP was necessary for transcription activation (147).
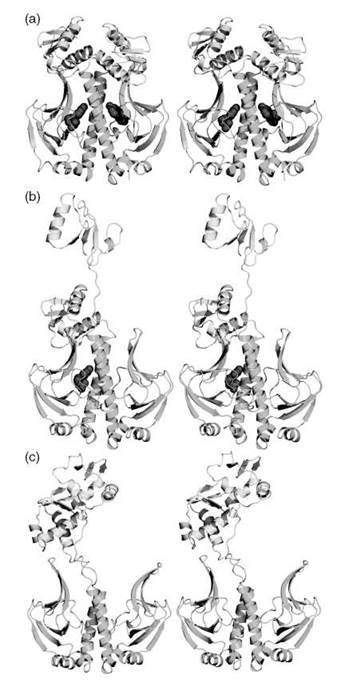
Figure 4. A stereoview of CAP dimer in (a) doubly liganded, (b) singly liganded, and (c) unliganded forms. The protein is rendered in cartoon representation, colored yellow for the DNA binding domain, and green for the ligand-binding domain. The cAMP ligands are depicted as red spheres.
The transglutaminase type 2 (TG2) enzyme is one example where a triggering event at a GTP-binding site causes alteration of catalysis at a distal site (133). TG2 is a multifunctional protein with roles in receptor signaling, extracellular matrix assembly, and apoptosis (Fig. 5) (133). The catalytic function of the enzyme, which consists of posttranslational amine modification of proteins or cross-linking of interchain glutamine and lysine residues (148), is allosterically controlled by calcium and GTP (149). But the three-dimensional structure of TG2 (Fig. 5) reveals that the binding site of GTP is located more than 20 A away from the catalytic center, which precludes any direct electrostatic or bonding interaction. It has been shown that transglutaminases exist in an active and inactive conformation, and that GTP binding promotes the formation of the active conformer (150). Recently, a study from Begg et al. (133) has suggested that an arginine residue (Ag-579) is critical for TG2 transition to a compact and inactive form. They suggest that the GTP-mediated conformational transition into inactive form is caused by the formation of a hydrogen bond with the catalytic residues of the active site Cys-277 and a tyrosine residue. They argue that GTP masks the charge of a nearby Arg-579, which promotes the Cys-277 and Tyr-516 hydrogen bond.

Figure 5. A stereoview of TG2 crystal structure with bound GDP. The TG2 structure is rendered in cartoon representation. The p-sandwich domain, catalytic core domain, first and second p-barrel domain is colored in green, red, blue, and yellow, respectively. The active and GDP molecule is rendered in cyan and orange spheres, respectively.
In other systems, the triggering event causes significant conformational change. The elongation factor Tu (EF-Tu) is one example in which the hydrolysis of a phosphoester bond from GTP causes interdomain separation within the protein (Fig. 6). EF-Tu is a member of the GTPase superfamily that guides aa-tRNA to the acyltranfer site (A site) of the ribosome, which mediates the accommodation step and initiation of the protein biosynthetic process (see Fig. 6a). Cognate recognition between the anticodon of the nascent tRNA and the codon of the mRNA in the ribosome causes GTP hydrolysis more than 50 A away in EF-Tu’s active site (Fig. 6b). The allosterically induced conformational change was rationalized as a series of perturbations that start from the GTP binding site that propagate into the nucleotide binding sites (domains II and III, see Fig. 6). It is not unconceivable that alteration in the shorter and longer timescale motions occur as a result of the hydrolysis of GTP. It is likely that the loss of a phosphate moiety will have the effect of increasing local fluctuations in the shorter timescale, which eventually permeates into the longer timescale motion, resulting in the separation of the domains, an entropically highly favorable process.
In many cases, dynamical events as a result of ligand binding involve multiple steps that combine conformational and dynamical changes. An example is a recent study that combined computational and experimental techniques to study the activation of gelatinase-2 (MMP-9), which is a zinc-based endopeptidase whose aberrant control has been implicated in various pathological processes, including cancer (151). The activation process consists of the removal of a ~ 100-residue peptide through proteolytic cleavage mediated by human kalikrein and involves the dissociation of a bond between a cysteine thiol and the catalytic zinc ion, which is a process known as the “cysteine switch.” A stopped-flow X-ray absorption analysis provided, for the first time, a detailed account of the coordination states of the zinc ion during the activation. The process was found to be triggered by binding of the kalikrein protease. It is interesting to note, however, that the binding site of kallikrein occurs at a distal site from the catalytic zinc ion. This finding suggests that alterations in dynamics and structure mediated by this interaction occur through an allosteric mechanism.

Figure 6. (a) Stereoview of the three-dimensional structure of EF-Tu/GTP complex. The protein is shown in ribbon representation, and domain I is colored in blue, whereas domains II, and III are shown in yellow. GTP is rendered in capped-sticks representation (P, O, C are shown in yellow, red, and white, respectively. Mg2+ is shown in orange spacefill representation. (b) Stereoview of the three-dimensional structure of the EF-Tu/GDP complex, which illustrates the remarkable conformational change that the protein undergoes as a result of GTP hydrolysis.
Conclusion
Despite the extensive amount of work that has been done toward understanding the molecular recognition process, the design of small molecules that exhibit potency to biological receptors remains a challenge. Most efforts to date have been driven by structure, often without the consideration of motion that is experienced by the receptor. Structure-based design often entails the addition of various moieties to improve affinity. The result, however, is that the affinity does not improve because of an effect known as entropy-enthalpy compensation. Incorporating entropic effects is essential for a complete description of the recognition process. The motion that develops because of entropy often leads to effects such as cooperativity and allostery, which add another level of complexity to the ligand design process.
References
1. Meroueh SO, Fisher JF, Schlegel HB, Mobashery S. Ab initio QM/MM study of class A beta-lactamase acylation: dual participation of Glu166 and Lys73 in a concerted base promotion of Ser70. J. Am. Chem. Soc. 2005; 127;15397-15407.
2. Drake MT, Shenoy SK, Lefkowitz RJ. Trafficking of G protein-coupled receptors. Circ. Res. 2006; 99:570-582.
3. Cross MJ, Dixelius J, Matsumoto T, Claesson-Welsh L. VEGF-receptor signal transduction. Trends Biochem. Sci. 2003; 28:488- 494.
4. Mitra K, Frank J. Ribosome dynamics: insights from atomic structure modeling into cryo-electron microscopy maps. Annu. Rev. Biophys. Biomol. 2006; 35:299-317.
5. Buckingham AD, Fowler PW, Hutson JM. Theoretical-studies of vanderwaals molecules and intermolecular forces. Chem. Rev. 1988; 88:963-988.
6. Frederick KK, Marlow MS, Valentine KG, Wand AJ. Conformational entropy in molecular recognition by proteins. Nature 2007; 448:325-329.
7. Lazaridis T. Solvent size vs cohesive energy as the origin of hydrophobicity. Acc. Chem. Res. 2001; 34:931-937.
8. Chandler D. Hydrophobicity: two faces of water. Nature 2002; 417:491.
9. Chandler D. Interfaces and the driving force of hydrophobic assembly. Nature 2005; 437:640-647.
10. Southall NT, Dill KA, Haymet ADJ. A view of the hydrophobic effect. J. Phys. Chem. B 2002; 106:2812-2812.
11. Dill KA, Bromberg S. Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology. 2003. Garland Science, New York.
12. Meroueh O, Hase WL. Dynamics of energy transfer in peptide-surface collisions. J. Am. Chem. Soc. 2002; 124:1524-1531.
13. Yu J, Ustach C, Kim HR. Platelet-derived growth factor signaling and human cancer. J. Biochem. Molec. Biol. 2003; 36:49-59.
14. Massova I, Kotra LP, Fridman R, Mobashery S. Matrix metallo-proteinases: structures, evolution, and diversification. FASEB J. 1998; 12:1075-1095.
15. Bose R, Holbert MA, Pickin KA, Cole PA. Protein tyrosine kinase-substrate interactions. Curr. Opin. Struct. Biol. 2006; 16:668-675.
16. Capdeville R, Buchdunger E, Zimmermann J, Matter A. Glivec (STI571, imatinib), a rationally developed, targeted anticancer drug. Nature Rev. 2002; 1:493-502.
17. Dearden JC. In silico prediction of ADMET properties: how far have we come? Exp. Opin. Drug Metab. Toxicol. 2007; 3:635-639.
18. Whitesides GM, Krishnamurthy VM. Designing ligands to bind proteins, Quart. Rev. Biophys. 2005; 38:385-395.
19. Block P, Sotriffer CA, Dramburg I, Klebe G. AffinDB: a freely accessible database of affinities for protein-ligand complexes from the PDB. Nucleic Acids Res. 2006; 34:D522-526.
20. Hu L, Benson ML, Smith RD, Lerner MG, Carlson HA. Binding MOAD (mother of all databases). Proteins 2005; 60:333-340.
21. Wang R, Fang X, Lu Y, Wang S. The PDBbind database: collection of binding affinities for protein-ligand complexes with known three-dimensional structures. J. Med. Chem. 2004; 47:2977-2980.
22. Chang CE, Chen W, Gilson MK. Ligand configurational entropy and protein binding. Proc. Natl. Acad. Sci. U.S.A. 2007; 104:1534-1539.
23. Shaked Z, Szajewski RP, Whitesides GM. Rates of thiol-disulfide interchange reactions involving proteins and kinetic measurements of thiol pKa values. Biochemistry 1980; 19:4156-4166.
24. Tanford C, Roxby R. Interpretation of protein titration curves. Application to lysozyme. Biochemistry 1972; 11:2192-2198.
25. Golemi-Kotra D, Meroueh SO, Kim C, Vakulenko SB, Bulychev A, Stemmler AJ, Stemmler TL, Mobashery S. The importance of a critical protonation state and the fate of the catalytic steps in class A beta-lactamases and penicillin-binding proteins. J. Biol. Chem. 2004; 279:34665-34673.
26. Meroueh SO, Minasov G, Lee W, Shoichet BK, Mobashery S. Structural aspects for evolution of beta-lactamases from penicillin-binding proteins. J. Am. Chem. Soc. 2003; 125:9612- 9618.
27. Fisher JF, Meroueh SO, Mobashery S. Bacterial resistance to beta-lactam antibiotics: compelling opportunism, compelling opportunity. Chem. Rev. 2005: 105:395-424.
28. Bosshard HR, Marti DN, Jelesarov I. Protein stabilization by salt bridges: concepts, experimental approaches and clarification of some misunderstandings, J Mol Recognit 2004; 17:1-16.
29. Honig BH, Hubbell WL. Stability of “salt bridges” in membrane proteins. Proc. Natl. Acad. Sci. U.S.A. 1984; 81:5412-5416.
30. Brown S, Meroueh SO, Fridman R, Mobashery S. Quest for selectivity in inhibition of matrix metalloproteinases. Curr. Topics Med. Chem. 2004; 4:1227-1238.
31. Dudev T, Lim C. Principles governing Mg, Ca, and Zn binding and selectivity in proteins. Chem. Rev. 2003; 103:773-787.
32. Kang C, Pratt DW. Structures, charge distributions, and dynamical properties of weakly bound complexes of aromatic molecules in their ground and electronically excited states. Internat. Rev. Phys. Chem. 2005; 24:1-36.
33. Piquemal JP, Chelli R, Procacci P, Gresh N. Key role of the polarization anisotropy of water in modeling classical polarizable force fields. J. Phys. Chem. A 2007; 111:8170-8176.
34. Jeffrey GA, Saenger W. Hydrogen Bonding in Biological Structure. 1991. Springer-Verlag, Berlin.
35. Scheiner S. Hydrogen Bonding: A Theoretical Perspective. 1997. Oxford University Press, New York.
36. Morozov AV, Kortemme T. Potential functions for hydrogen bonds in protein structure prediction and design. Adv. Prot. Chem. 2005; 72:1-38.
37. Stone AJ. chapRecent Theoretical and Experimental Advances in Hydrogen Bonded Clusters. Xantheas SS, ed. 2000. Kluwer Academic, Boston, MA. pp.25-34.
38. Panigrahi SK, Desiraju GR. Strong and weak hydrogen bonds in the protein-ligand interface. Proteins 2007; 67:128-141.
39. Wahl MC, Sundaralingam M. C-H center dot center dot center dot O hydrogen bonding in biology. Trends Biochem. Sci. 1997; 22:97-102.
40. Desiraju GR, Steiner T. The Weak Hydrogen Bond in Structural Chemistry and Biology, Volume 29-121. 1999. Oxford University Press, New York.
41. Manikandan K, Ramakumar S. The occurrence of C-H center dot center dot center dot O hydrogen bonds in alpha-helices and helix termini in globular proteins. Prot.-Struct. Funct. Bioinformat. 2004; 56:768-781.
42. Scheiner S, Kar T. Effect of solvent upon CH center dot center dot center dot O hydrogen bonds with implications for protein folding. J. Phys. Chem. B 2005; 109:3681-3689.
43. Auffinger P, Hays FA, Westhof E, Ho PS. Halogen bonds in biological molecules. Proc. Natl. Acad. Sci. U.S.A. 2004; 101:16789-16794.
44. Prabhu N, Sharp K. Protein-solvent interactions. Chem. Rev. 2006; 106:1616-1623.
45. Kauzmann W. Some factors in the interpretation of protein denaturation, Adv. Prot. Chem. 1959; 14:1-63.
46. Muller N. Search for a realistic view of hydrophobic effects. Acc. Chem. Res. 1990; 23:23-28.
47. Dill KA. Dominant forces in protein folding. Biochemistry 1990; 29:7133-7155.
48. Smithrud DB, Wyman TB, Diederich F. Enthalpically driven cyclophane arene inclusion complexation - Solvent-dependent calorimetric studies. J. Am. Chem. Soc. 1991; 113:5420-5426.
49. Gilson MK, Zhou HX. Calculation of protein-ligand binding affinities. Annu. Rev. Biophys. Biomol. Struct. 2007; 36:21-42.
50. Karplus M, McCammon JA. Molecular dynamics simulations of biomolecules. Nat Struct Biol 2002;9:646-652.
51. Meng EC, Shoichet BK, Kuntz ID. Automated docking with grid-based energy evaluation. J. Computat. Chem. 1992; 13:505- 524.
52. Kitchen DB, Decornez H, Furr JR, Bajorath J. Docking and scoring in virtual screening for drug discovery: methods and applications. Nature Rev. 2004; 3:935-949.
53. Perola E, Walters WP, Charifson PS. A detailed comparison of current docking and scoring methods on systems of pharmaceutical relevance. Proteins 2004; 56:235-249.
54. Berendsen HJC, Vanderspoel D, Vandrunen R. Gromacs - a message-passing parallel molecular-dynamics implementation. Comput. Phys. Communicat. 1995; 91:43-56.
55. Goodsell DS, Morris GM, Olson AJ. Automated docking of flexible ligands: applications of AutoDock. J. Mol. Recognit. 1996; 9:1-5.
56. Rarey M, Kramer B, Lengauer T, Klebe G. A fast flexible docking method using an incremental construction algorithm. J. Molec. Biol. 1996; 261:470-489.
57. Shoichet BK. Virtual screening of chemical libraries. Nature 2004; 432:862-865.
58. Bohm HJ. The development of a simple empirical scoring function to estimate the binding constant for a protein-ligand complex of known three-dimensional structure. J. Computer-Aided Molec. Design 1994; 8:243-256.
59. Eldridge MD, Murray CW, Auton TR, Paolini GV, Mee RP. Empirical scoring functions: I. The development of a fast empirical scoring function to estimate the binding affinity of ligands in receptor complexes. J. Computer-Aided Molec. Design 1997; 11:425-445.
60. Bohm HJ. Prediction of binding constants of protein ligands: a fast method for the prioritization of hits obtained from de novo design or 3D database search programs. J. Computer-Aided Molec. Design 1998; 12:309-323.
61. Muegge I, Martin YC. A general and fast scoring function for protein-ligand interactions: a simplified potential approach. J. Med. Chem. 1999; 42:791-804.
62. Muegge I. PMF scoring revisited. J. Med. Chem. 2006; 49:5895-5902.
63. Gohlke H, Hendlich M, Klebe G. Knowledge-based scoring function to predict protein-ligand interactions. J. Molec. Biol. 2000; 295:337-356.
64. Velec HF, Gohlke H, Klebe G. DrugScore(CSD)-knowledge-based scoring function derived from small molecule crystal data with superior recognition rate of near-native ligand poses and better affinity prediction, J. Med. Chem. 2005; 48:6296-6303.
65. Huey R, Morris GM, Olson AJ, Goodsell DS. A semiempirical free energy force field with charge-based desolvation. J. Computat. Chem. 2007; 28:1145-1152.
66. Jones G, Willett P, Glen RC. A genetic algorithm for flexible molecular overlay and pharmacophore elucidation, J Comput Aid Mol Des 1995; 9:532-549.
67. Jones G, Willett P, Glen RC, Leach AR, Taylor R. Development and validation of a genetic algorithm for flexible docking. J. Molec. Biol. 1997; 267:727-748.
68. Ponder JW, Case DA. Force fields for protein simulations. Adv. Prot. Chem. 2003; 66:27-85.
69. Karplus M, McCammon JA. Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 2002; 9:646-652.
70. Cavasotto CN, Kovacs JA, Abagyan RA. Representing receptor flexibility in ligand docking through relevant normal modes. J. Am. Chem. Soc. 2005; 127:9632-9640.
71. Case DA, T. A. D., Cheatham III TE, Simmerling CL, Wang J, Duke RE, Luo R, Merz KM, Wang B, Pearlman DA, Crowley M, Brozell S, Tsui V, Gohlke H, Mongan J, Hornak V, Cui G, Beroza P, Schafmeister C, Caldwell JW, Ross WS, Kollman PA. AMBER 8. 2004 University of California, San Francisco.
72. Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comp. Chem. 1983; 4:187-217.
73. Lindahl E, Hess B, van der Spoel D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Molec. Model. 2001; 7:306-317.
74. Marelius J, Hansson T, Aqvist J. Calculation of ligand binding free energies from molecular dynamics simulations. Internat. J. Quantum Chem. 1998; 69:77-88.
75. Jorgensen WL, Ruiz-Caro J, Tirado-Rives J, Basavapathruni A, Anderson KS, Hamilton AD. Computer-aided design of non-nucleoside inhibitors of HIV-1 reverse transcriptase. Bioorg. Med. Chem. Lett. 2006; 16:663-667.
76. Zhang W, Shi Q, Meroueh SO, Vakulenko SB, Mobashery S. Catalytic mechanism of penicillin-binding protein 5 of Escherichia coli. J. Biol. Chem. 2007; 46:10113-10121.
77. Case DA. Molecular dynamics and NMR spin relaxation in proteins. Acc. Chem. Res. 2002; 35:325-331.
78. Hansson T, Oostenbrink C, van Gunsteren WF. Molecular dynamics simulations. Curr. Opin. Struct. Biol. 2002; 12:190-196.
79. Kollman PA, Massova I, Reyes C, Kuhn B, Huo SH, Chong L, Lee M, Lee T, Duan Y, Wang W, Donini O, Cieplak P, Srinivasan J, Case DA, Cheatham TE. Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. Acc. Chem. Res. 2000; 33:889-897.
80. Wang JM, Morin P, Wang W, Kollman PA. Use of MM-PBSA in reproducing the binding free energies to HIV-1 RT of TIBO derivatives and predicting the binding mode to HIV-1 RT of efavirenz by docking and MM-PBSA. J. Am. Chem. Soc. 2001; 123:5221-5230.
81. Aqvist J, Medina C, Samuelsson JE. New method for predicting binding-affinity in computer-aided drug design. Prot. Engineer. 1994; 7:385-391.
82. Xu Y, Wang RX. A computational analysis of the binding affinities of FKBP12 inhibitors using the MM-PB/SA method. Prot.-Struct. Funct. Bioinformat. 2006; 64:1058-1068.
83. Gohlke H, Case DA. Converging free energy estimates: MM-PB(GB)SA studies on the protein-protein complex Ras-Raf. J. Computat. Chem. 2004; 25:238-250.
84. Wan SZ, Coveney PV, Flower DR. Peptide recognition by the T cell receptor: comparison of binding free energies from thermodynamic integration, Poisson-Boltzmann and linear interaction energy approximations. Philos. Trans. Royal Soc. Mathemat. Phys. Engineer. Sci. 2005; 363:2037-2053.
85. Frauenfelder H, Sligar SG, Wolynes PG. The energy landscapes and motions of proteins. Science 1991; 254:1598-1603.
86. Karplus M, Kuriyan J. Molecular dynamics and protein function. Proc. Natl. Acad. Sci. U.S.A. 2005; 102:6679-6685.
87. Popovych N, Sun SJ, Ebright RH, Kalodimos CG. Dynamically driven protein allostery. Nat. Struct. Molec. Biol. 2006; 13:831- 838.
88. Henzler-Wildman KA, Lei M, Thai V, Kerns SJ, Karplus M, Kern D. A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature 2007; 450:913-916.
89. Henzler-Wildman KA, Thai V, Lei M, Ott M., Wolf-Watz M, Fenn T, Pozharski E, Wilson MA, Petsko GA, Karplus M, Hubner CG, Kern D. Intrinsic motions along an enzymatic reaction trajectory. Nature 2007; 450:838-U813.
90. Keramisanou D, Biris N, Gelis I, Sianidis G, Karamanou S, Economou A, Kalodimos CG. Disorder-order folding transitions underlie catalysis in the helicase motor of SecA. Nature Struct. Molec. Biol. 2006; 13:594-602.
91. Boehr DD, McElheny D, Dyson HJ, Wright PE. The dynamic energy landscape of dihydrofolate reductase catalysis. Science 2006; 313:1638-1642.
92. Boehr DD, McElheny D, Dyson HJ, Wright PE. Substrate-specific us-ms time-scale motions in the E. coli dihydrofolate reductase: NADPH complex. FASEB J. 2005; 19:A846-A847.
93. Bowman AL, Nikolovska-Coleska Z, Zhong H, Wang S, Carlson HA. Small molecule inhibitors of the MDM2-p53 interaction discovered by ensemble-based receptor models. J. Am. Chem. Soc. 2007; 129:12809-12814.
94. Yang CY, Wang RX, Wang SM. M-score: a knowledge-based potential scoring function accounting for protein atom mobility. J. Med. Chem. 2006; 49:5903-5911.
95. Kallblad P, Dean PM. Efficient conformational sampling of local side-chain flexibility. J. Molec. Biol. 2003; 326:1651-1665.
96. Sherman W, Day T, Jacobson MP, Friesner RA, Farid R. Novel procedure for modeling ligand/receptor induced fit effects. J. Med. Chem. 2006; 49:534-553.
97. Fischer E. Einfluss der configuration auf die wirkung den enzyme. Ber. Dtsch. Chem. Ges. 1894; 27:2985-2993.
98. Najmanovich R, Kuttner J, Sobolev V, Edelman M. Side-chain flexibility in proteins upon ligand binding. Proteins 2000; 39:261-268.
99. Ma BY, Shatsky M, Wolfson HJ, Nussinov R. Multiple diverse ligands binding at a single protein site: a matter of pre-existing populations. Protein Sci. 2002; 11:184-197.
100. Gutteridge A, Thornton J. Conformational changes observed in enzyme crystal structures upon substrate binding. J. Molec. Biol. 2005; 346:21-28.
101. Koshland DE. Application of a theory of enzyme specificity to protein synthesis. Proc. Natl. Acad. Sci. U.S.A. 1958; 44:98-104.
102. Volkman BF, Lipson D, Wemmer DE, Kern D. Two-state allosteric behavior in a single-domain signaling protein. Science 2001; 291;2429-2433.
103. Popovych N, Sun S, Ebright RH, Kalodimos CG. Dynamically driven protein allostery, Nature struct. Molec. Biol. 2006; 13:831-838.
104. Gakamsky DM, Lewitzki E, Grell E, Saulquin X, Malissen B, Montero-Julian F, Bonneville M, Pecht I. Kinetic evidence for a ligand-binding-induced conformational transition in the T cell receptor. Proc. Natl. Acad. Sci. U.S.A. 2007; 104:16639-16644.
105. Monod J, Wyman J, Changeux JP. On the nature of allosteric transitions: a plausible model. J. Molec. Biol. 1965; 12:88-118.
106. Hecht JL, Honig B, Shin YK, Hubbell WL. Electrostatic potentials near-the-surface of DNA - comparing theory and experiment. J. Phys. Chem. 1995; 99:7782-7786.
107. Miller DW, Dill KA. Ligand binding to proteins: the binding landscape model. Protein Sci. 1997; 6:2166-2179.
108. Foote J, Milstein C. Conformational isomerism and the diversity of antibodies. Proc. Natl. Acad. Sci. U.S.A. 1994; 91;10370-10374.
109. James LC, Roversi P, Tawfik DS. Antibody multispecificity mediated by conformational diversity. Science 2003; 299:1362-1367.
110. Tobi D, Bahar I. Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state. Proc. Natl. Acad. Sci. U.S.A. 2005; 102:18908-18913.
111. Chow CS, Bogdan FM. A structural basis for RNA-ligand interactions. Chem. Rev. 1997; 97:1489-1513.
112. Carter AP, Clemons WM, Brodersen DE, Morgan-Warren RJ, Wimberly BT, Ramakrishnan V. Functional insights from the structure of the 30S ribosomal subunit and its interactions with antibiotics. Nature 2000; 407:340-348.
113. Meroueh SO, Mobashery S. Conformational transition in the aminoacyl t-RNA site of the bacterial ribosome both in the presence and absence of an aminoglycoside antibiotic. Chem. Biol. Drug Design 2007; 69:291-297.
114. Dunitz JD. Win some, lose some: enthalpy-entropy compensation in weak intermolecular interactions. Chem. Biol. 1995; 2:709- 712.
115. Searle MS, Westwell MS, Williams DH. Application of a generalized enthalpy-entropy relationship to binding cooperativity and weak associations in solution. J. Chem. Soc. Perk. T 1995; 2:141-151.
116. Gilli P, Ferretti V, Gilli G, Borea PA. Enthalpy-entropy compensation in drug-receptor binding. J. Phys. Chem. 1994; 98:1515-1518.
117. Sharp K. Entropy-enthalpy compensation: fact or artifact? Protein Sci. 2001; 10:661-667.
118. Lafont V, Armstrong AA, Ohtaka H, Kiso Y, Amzel LM, Freire E. Compensating enthalpic and entropic changes hinder binding affinity optimization. Chem. Biol. Drug Design 2007; 69:413-422.
119. Rekharsky M, Hesek D, Lee M, Meroueh SO, Inoue Y, Mobashery S. Thermodynamics of interactions of vancomycin and synthetic surrogates of bacterial cell wall. J. Am. Chem. Soc. 2006; 128:7736-7737.
120. Cornish-Bowden A. Enthalpy-entropy compensation: a phantom phenomenon. J. Biosci. 2002; 27:121-126.
121. Liu Y, Sturtevant JM. Significant discrepancies between van’t Hoff and calorimetric enthalpies. Biophys. Chem. 1997; 64:121- 126.
122. Li L, O’Callaghan B, Dantzer J, Meroueh SO. PDBcal: a comprehensive dataset with three-dimensional structures and thermodynamics data from isothermal titration calorimetry. J. Med. Chem. In Press.
123. Ford DM. Enthalpy-entropy compensation is not a general feature of weak association. J. Am. Chem. Soc. 2005; 127:16167-16170.
124. Cooper A. Thermodynamic analysis of biomolecular interactions. Curr. Opin. Chem. Biol. 1999; 3:557-563.
125. Jen-Jacobson L, Engler LE, Ames JT, Kurpiewskim MR, Grigorescu A. Thermodynamic parameters of specific and nonspecific protein-DNA binding. Supramolec. Chem. 2000; 12,143-160.
126. Tyuma I, Imai K, Shimizu K. Analysis of oxygen equilibrium of hemoglobin and control mechanism of organic phosphates. Biochemistry 1973; 12:1491-1498.
127. Kern D, Zuiderweg ER. The role of dynamics in allosteric regulation. Curr. Opin. Struct. Biol. 2003; 13:748-757.
128. Daily MD, Gray JJ. Local motions in a benchmark of allosteric proteins. Proteins-Struct. Funct. Bioinformat. 2007; 67:385-399.
129. Thordarson P, Bijsterveld EJA, Elemans JAAW, Kasak P, Nolte RJM, Rowan AE. Highly negative homotropic allosteric binding of viologens in a double-cavity porphyrin. J. Am. Chem. Soc. 2003; 125:1186-1187.
130. Kawai H, Katoono R, Nishimura K, Matsuda S, Fujiwara K, Tsuji T, Suzuki T. Positive homotropic allosteric binding of benzenediols in a hydrindacene-based exoditopic receptor: co- operativity in amide hydrogen bonding. J. Am. Chem. Soc. 2004; 126:5034-5035.
131. Di Cera E, Page MJ, Bah A, Bush-Pelc LA, Garvey LC. Thrombin allostery. Phys. Chem. Chemical Phys. 2007; 9:1291-1306.
132. Li L, Uversky VN, Dunker AK, Meroueh SO. Computational investigation of allostery in the catabolite activator protein. J. Am. Chem. Soc. 2007; 129:15668-15676.
133. Begg GE, Carrington L, Stokes PH, Matthews JM, Wouters MA, Husain A, Lorand L, Iismaa SE, Graham RM. Mechanism of allosteric regulation of transglutaminase 2 by GTP. Proc. Natl. Acad. Sci. U.S.A. 2006; 103:1968-19688.
134. Fabris D, Fenselau C. Characterization of allosteric insulin hexamers by electrospray ionization mass spectrometry. Anal. Chem. 1999; 71:384-387.
135. Yan Z, Chang Y, Mayo D, Maslak V, Xia S, Badjic JD. Allosteric regulation of the conformational dynamics of a cavitand receptor. Organic Lett. 2006; 8:3697-3700.
136. Kim J, Raushel FM. Allosteric control of the oligomerization of carbamoyl phosphate synthetase from Escherichia coli. Biochemistry 2001; 40:11030-11036.
137. Daily MD, Gray JJ. Local motions in a benchmark of allosteric proteins. Proteins 2007; 67:385-399.
138. Peratz MF, Wilkinson AJ, Paoli M, Dodson GG. The stereochemical mechanism of the cooperative effects in hemoglobin revisited. Annu. Rev. Biophys. Biomol. Struct. 1998; 27:1-34.
139. Perutz MF. Stereochemistry of cooperative effects in haemoglobin. Nature 1970; 228:726-739.
140. Pawlyk AC, Pettigrew DW. Transplanting allosteric control of enzyme activity by protein-protein interactions: coupling a regulatory site to the conserved catalytic core. Proc. Natl. Acad. Sci. U.S.A. 2002; 99:11115-11120.
141. Holtman CK, Pawlyk AC, Meadow N, Roseman S, Pettigrew DW. IIA(Glc) allosteric control of Escherichia coli glycerol kinase: binding site cooperative transitions and cation-promoted association by Zinc(II). Biochemistry 2001; 40:14302-14308.
142. Alexander RW, Schimmel P. Evidence for breaking domain-domain functional communication in a synthetase-tRNA complex. Biochemistry 1999; 38:16359-16365.
143. Meroueh SO, Roblin P, Golemi D, Maveyraud L, Vakulenko SB, Zhang Y, Samama JP, Mobashery S. Molecular dynamics at the root of expansion of function in the M69L inhibitor-resistant TEM beta-lactamase from Escherichia coli. J. Am. Chem. Soc. 2002; 124:9422-9430.
144. Heyduk T, Lee JC. Escherichia-coli camp receptor protein - evidence for 3 protein conformational states with different promoter binding affinities. Biochemistry 1989; 28:6914-6924.
145. Leu SF, Baker CH, Lee EJ, Harman JG. Position 127 amino acid substitutions affect the formation of CRP: cAMP: lacP complexes but not CRP: cAMP: RNA polymerase complexes at lacP. Biochemistry 1999; 38:6222-6230.
146. Takahashi M, Blazy B, Baudras A, Hillen W. Ligand-modulated binding of a gene regulatory protein to DNA. Quantitative analysis of cyclic-AMP induced binding of CRP from Escherichia coli to non-specific and specific DNA targets. J. Molec. Biol. 1989; 207:783-796.
147. Harman JG. Allosteric regulation of the cAMP receptor protein. Bba-Protein Struct. M 2001; 1547:1-17.
148. Lorand L, Graham RM. Transglutaminases: crosslinking enzymes with pleiotropic functions. Nature Rev. 2003; 4:140-156.
149. Achyuthan KE, Greenberg CS. Identification of a guanosine triphosphate-binding site on guinea pig liver transglutaminase. Role of GTP and calcium ions in modulating activity. J. Biol. Chem. 1987; 262:1901-1906.
150. Ahvazi B, Kim HC, Kee SH, Nemes Z, Steinert PM. Threedimensional structure of the human transglutaminase 3 enzyme: binding of calcium ions changes structure for activation. EMBO J. 2002; 21:2055-2067.
151. Rosenblum G, Meroueh S, Toth M, Fisher JF, Fridman R, Mobashery S, Sagi I. Molecular structures and dynamics of the stepwise activation mechanism of a matrix metalloproteinase zymogen: challenging the cysteine switch dogma. J. Am. Chem. Soc. 2007; 129:13566-13574.