CHEMICAL BIOLOGY

Transient State Enzyme Kinetics

Kenneth A. Johnson, Department of Chemistry and Biochemistry, Institute for Cellular and Molecular Biology, University of Texas at Austin, Austin, Texas

doi: 10.1002/9780470048672.wecb609

Transient-state kinetic analysis defines the elementary steps along the pathway of an enzyme-catalyzed reaction. The methods rely on rapidly mixing a substrate with a sufficient concentration of enzyme to allow a direct observation of intermediates and products formed at the active site during a single enzyme cycle. Stopped-flow methods afford observation of reactions by monitoring changes in optical signals (i.e., absorbance, fluorescence, and light scattering) as a function of time after mixing. Analysis of the substrate concentration dependence of the rates and the amplitudes of observable species can define the sequence of events that occur after substrate binding. Rapid-chemical quench-flow methods require two sequential mixing events: one to start the reaction and a second to stop the reaction by the addition of a quenching agent. One then quantifies the amount of product formed, often by chromatography, to resolve radiolabeled substrate from the product. Because one can observe the conversion of substrate to product directly on a known concentration scale, rapid quench experiments can be interpreted directly. In the final analysis, the most rigorous interpretation relies on global analysis fitting both stopped-flow and rapid quench-flow data simultaneously to establish a reaction pathway and the rates of interconversion of kinetically significant intermediates. Accordingly, transient-state kinetic methods allow a definition of a reaction sequence by direct measurement of each step to establish the kinetic and thermodynamic basis for enzyme specificity and efficiency.

Structural and kinetic methods provide a powerful combination of related data to explore the remarkable efficiency and specificity of enzymes. Each method fills in details left out from the other. Structural studies provide a static picture, whereas kinetics bring the structure to life by providing the data to define the dynamics that underlie catalysis. To relate kinetic studies directly to structure, it is crucial to examine the reactions that occur at the active site of the enzyme, namely, after substrate binding and before product release. Unfortunately, steady-state kinetic methods cannot reveal details regarding the conversion of substrate to product at the active site of an enzyme. Therefore, we turn to rapid-transient kinetic methods in which we examine the enzyme as a stoichiometric reactant rather than as a trace catalyst. We can thereby observe enzyme-bound species formed during catalysis by examining the time scale of a single enzyme turnover. The reactions that govern enzyme specificity and efficiency can then be defined by quantifying the rates of substrate binding, enzyme isomerization, chemical conversion of substrate to product, and product release.

Measurable Kinetic Parameters

Traditional steady-state kinetic studies rely on indirect observation of catalysis by monitoring the accumulation of product or consumption of substrate as a consequence of many reaction cycles with a trace of catalyst. Conclusions are limited to inference of the possible pathways for the order of addition of multiple substrates and release of products and quantification of two bulk kinetic parameters, k_cat and k_cat/K_m. The parameter k _cat defines the maximum rate of conversion of enzyme-bound substrate to product released into solution, but it cannot be used to establish whether the maximum rate of reaction is limited by enzyme conformational changes, rates of chemical reaction, or rates of product release per se; it does, however, set a lower limit on the magnitude of any rate constant in that sequence. The term k_cat/K_m is known as the specificity constant because it quantifies which enzyme or substrate wins in a competition. Moreover, k_cat/K_m defines the rate of substrate binding multiplied by the probability that once bound, the substrate is converted to product and released. As such, k_cat/k_cat/K_m sets a lower limit on the second-order rate constant for substrate binding, and it also provides a measure of enzyme efficiency relative to the diffusion-limited substrate-binding rate. The term K_m is best understood as the ratio between the two primary parameters, k_cat, and k_cat/K_m, and it is generally not equal to the dissociation constant for substrate binding. These steady-state kinetic parameters form the minimal background to design experiments than can define the sequence of individual steps along the reaction pathway.

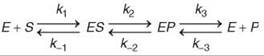
Transient-state kinetic analysis allows definition of a minimal reaction sequence of kinetically significant intermediates responsible for the conversion of substrate to product at the enzyme active site (1). Resolution of how individual rate constants lead to a given value for k_cat/K_m provides an understanding of the reactions that govern enzyme specificity and efficiency. Direct measurement of events that occur at the active site of the enzyme fills the void of information left by steady state kinetic studies, namely, the steps that occur after substrate binding through to the point of product release. Using transient kinetic methods, the rates of a single reaction cycle are measured using an enzyme as an observable reactant often at concentrations approximately equal to the substrate. For example, given the pathway shown in Scheme 1, all eight rate constants can be measured by a combination of equilibrium, steady-state, and transient-state kinetic experiments. Moreover, these kinetic studies lay the foundation for the identification of enzyme bound intermediates (EI).

Scheme 1.

Comprehensive kinetic analysis defines the mechanistic basis for enzyme specificity and efficiency in ways that can be directly related to enzyme structure. In this article, the rationale will be described for design and interpretation of experiments to define the pathway of enzyme-catalyzed reactions using transient kinetic methods. These principles will be illustrated with three examples of biologically important reactions, none of which could have been solved with steady-state kinetics alone. This article is by no means a comprehensive survey of this extensive field, but rather, selected examples from the author’s laboratory will be used to illustrate the methods to provide a flavor for what is possible.

Transient Kinetics of Biological Reactions

Enzyme catalysis is the basis for life. Enzymes accelerate desired reactions so they occur on a time scale requisite for living organisms. Moreover, enzymes can synthesize complex biological macromolecules that exist long enough to sustain life by coupling desired synthetic reactions to thermodynamically favorable catabolic reactions. Kinetic analysis allows us to decipher the pathway by which enzymes carry out these biologically important reactions with incredible speed, efficiency, and specificity. Traditional steady-state kinetic methods provide estimates for the kinetic constants, k_catand k_cat/K_m, which govern the flux through metabolic pathways. Transient-state kinetic methods allow definition of the kinetically significant reaction sequence and can provide estimates for each intrinsic rate constant along the pathway, including rates of formation and breakdown of enzyme-bound intermediates. Thus, transient-state kinetic analysis is essential to understanding how enzymes bring about catalysis. Here, three examples of biologically important reactions are provided.

DNA polymerase fidelity

As one example, we have long been fascinated by the incredible speed and accuracy of DNA polymerases that can replicate DNA at a rate of 300 base pairs per second while introducing errors only 1 out of a billion times (2). Kinetic analysis has revealed how these enzymes use information from both hydrogen bonding and shape of the base pair to discriminate correct base pairs from the three possible competing mismatches at any DNA template position (3-6). The most important step in which specificity is determined is during a change in enzyme structure after nucleotide binding, in which substrate binding energy is used to alter the enzyme conformation. After the conformational change, a correct substrate (deoxynucleotide) becomes tightly bound in a state that slows release of the bound substrate and organizes the active site residues to promote catalysis. In contrast, an incorrect substrate (a mismatched deoxynucleotide) disorganizes the active site residues leading to a state that promotes release of the substrate and slows the chemical reaction. Thus, it is the kinetic partitioning of the conformational isomer formed after substrate binding that establishes substrate specificity. Transient-state kinetic analysis has revealed how these structural dynamics endow the polymerase with the ability to replicate DNA with sufficient accuracy and speed to sustain a living organism.

Detection of enzyme intermediates

Enzymes often catalyze conversion of a substrate to product through a sequence of intermediate states. In many instances, the intermediates must be inferred because they are not sufficiently stable kinetically or thermodynamically to be observed directly. However, in several instances, transient-state kinetic analysis has allowed identification of enzyme-bound intermediates. Rigorous kinetic analysis is essential to distinguish intermediates from the side products of the reaction. As one example, excitatory postsynaptic potential (EPSP) synthase, which is the target of the herbicide glyphosate, catalyzes the reaction of shikimate-3-phosphate (S3P) with phosphoenolpyruvate (PEP) through a tetrahedral intermediate to form the product, EPSP (7, 8). The mechanism of the reaction is crucial for understanding the mode of inhibition by glyphosate and in the quest for more effective herbicides. Transient-state kinetic studies revealed the rapid formation and breakdown of the intermediate in less than 100 milliseconds. In contrast, structural studies by nuclear magnetic resonance suggested another species (EPSP ketal) as an intermediate, but subsequent kinetic analysis showed that its rate of formation at the active site was a million-fold too slow to account for catalysis (9, 10). Thus, kinetic competence is a critical criterion for the identification of intermediates; the intermediate must be formed and broken down at rates sufficient to account for the net conversion of substrate to product at the enzyme active site (11). Single-turnover transient-state kinetic studies provide the crucial data to identify enzyme intermediates.

Force production by motor proteins

Motor proteins such as myosin, dynein, and kinesin, produce a force for movement by coupling the hydrolysis of ATP to conformational changes in protein structure that are linked to the cyclical interaction of the motor with a filament (actin or microtubules). Initial characterization of actin-stimulated myosin ATPase kinetics using steady-state methods led to the puzzling observation that actin fully simulated ATP turnover while associating with only small fraction of the myosin (12). In a set of simple and direct experiments using transient kinetics, Lymn and Taylor (13) showed that actin associates with myosin for a very brief time and then rapidly dissociates as part of the myosin crossbridge cycle. ATP binding to the actomyosin complex stimulates rapid release of the myosin from the actin, whereas the binding of actin to the myosin-ADP-P complex simulates the release of products (ADP and P). Conformational changes that occur with nucleotide binding and release are then coupled to force production. Another motor protein, which is called kinesin, walks along microtubules in a hand-over-hand fashion because of an alternating-site ATPase pathway (14, 15). Strain in the linkage between the two motor domains of this dimeric protein distinguishes leading from lagging ATPase sites when they are both bound to the microtubule surface. This strain leads to rapid dissociation of ADP from the leading motor domain while stimulating ATP hydrolysis on the lagging motor domain. Moreover, ATP binding to the lagging head stimulates the release of ADP from the leading head. Transient kinetic analysis established this alternating site ATPase cycle by showing directly that ATP binding to one site simulated the rate of ADP release from the other site (14).

Kinetic and Structural Basis for Catalysis

Structural analysis is often the basis for discussions of enzyme specificity and mechanism. However, structural studies alone cannot establish mechanism or define the origins of enzyme specificity. In the three examples cited above, structural studies were critical to illustrate the active site residues, but could not by themselves address the most pressing questions. In particular, enzyme specificity is a kinetic phenomenon which is quantified by k_cat/K_m, but the underlying origins of specificity are not revealed by pondering the magnitude of k_cat/K_m or by inspecting the three-dimensional arrangements of amino acids. Rather, in combination with transient-state kinetic studies, the structures and steady-state kinetic parameters take on new meaning and can be interpreted to reveal fascinating details of enzyme dynamics and specificity.

The chemistry of DNA polymerization

The structure of the active site of a DNA polymerase with bound DNA and an incoming substrate, dCTP, is shown in Fig. 1a (16). In this structure, the DNA is terminated with a dideoxynu- cleotide that lacks the 3’OH so that catalysis is prevented, and so this structure is thought to represent a close approximation to the closed enzyme state immediately preceding catalysis. The chemistry of the reaction is well established in that the reaction is catalyzed by a two metal ion mechanisms, in which one Mg⁺² increases the nucleophilic reactivity of the 3’OH while the other Mg⁺² stabilizes the developing negative charge on the a-phosphate during the transition state (17). However, this model does not explain the extraordinary efficiency and specificity of the reaction. This polymerase copies DNA at a rate of 300 base pairs per second and makes a mistake approximately one out of a million times. After making a mistake, the polymerase stalls, which gives time for the DNA primer strand to melt away from the template strand and migrate to an exonuclease site 25 Aaway to remove the mismatched base. The primer then rapidly reanneals and polymerization continues so that the overall error frequency is only one in a billion (5). Efficiency and specificity are kinetic properties of the enzyme that can be addressed directly by transient kinetic analysis to define the kinetically significant intermediates in the reaction sequence and thereby establish the kinetic and thermodynamic basis for nucleotide selectivity. Detailed kinetic studies have revealed that although the metal ions mechanism accounts for a base level of catalysis, the alignment of positively charged amino acids on the O-helix (Fig. 1a) plays a critical role in specificity by their involvement in recognition of a correct base pair.

Figure 1. Mechanism of DNA polymerization. (a) The structure of T7 DNA polymerase in a complex with DNA and an incoming nucleotide is shown with a fluorescent label attached to C514. Changes in the fluorescence allow quantification of the nucleotide-induced change in structure and its role in selectivity. Residues 233-411 and 436-454 have been removed to reveal the active site. Shown also are the O-helix and key catalytic residues From PDB 1 T7P (17). (b) The time dependence of the fluorescence change induced by nucleotide binding is shown at three concentrations of dCTP. The inset shows the measurement of the rate of dCTP dissociation from the E.DNA_dd.dNTP complex. Analysis of these data defined the role of enzyme conformational changes in nucleotide selectivity. Both figures are reproduced with permission from Reference 6.

The chemistry of EPSP synthase

EPSP synthase catalyzes the synthesis of EPSP by an addition-elimination reaction through the tetrahedral intermediate shown in Fig. 2a. This enzyme is on the shikimate pathway for synthesis of aromatic amino acids and is the target for the important herbicide, glyphosate, which is the active ingredient in Roundup (The Scotts Company LLC, Marysville, OH). Transient-state kinetic studies led to proof of this reaction mechanism by the observation and isolation of the tetrahedral intermediate. Moreover, quantification of the rates of formation and decay of the tetrahedral intermediate established that it was truly an intermediate species on the pathway between the substrates (S3P and PEP) and products (EPSP and Pi) of the reaction. The chemistry of this reaction is interesting in that the enzyme must first catalyze the formation of the intermediate and then catalyze its breakdown, apparently with different requirements for catalysis. Quantification of the rates of each step of this reaction in the forward and reverse directions has afforded a complete description of the free-energy profile for the reaction and allows estimation of the extent to which the enzyme catalyzes each step (8).

Figure 2. Intermediate in the EPSP synthase pathway. (a) The mechanism of the reaction catalyzed by EPSP synthase is shown. The reaction proceeds by an addition-elimination mechanism via a stable tetrahedral intermediate. (b) A single turnover reaction is shown in which 10-μM enzyme was mixed with 100-μM S3P and 3.5-μM radiolabeled PEP. Analysis by rapid-quench kinetic methods showed the reaction of PEP to form the intermediate, which then decayed to form EPSP in a single turnover. The smooth lines were computed from a complete model by numerical integration of the equations based on a global fit to all available data. Reproduced with permission from Reference 7.

The chemistry of energy transduction by motor proteins

The free energy available from the hydrolysis of ATP to form ADP and Pi in solution is generally in the neighborhood of 15 kcal/mol, depending of course, on the intracellular concentrations of ATP, ADP, and Pi. The means by which an enzyme can couple this free energy to produce a force for movement has been the topic of research for more than a half century. Studies in the light microscope established a sliding filament model for muscle contraction, which was subsequently shown to be caused by the cyclical interaction of the myosin AT-Pase with actin filaments. A major revelation came with the realization that the largest changes in free energy are associated with the binding of ATP and the release of ADP and Pi, whereas the actual chemical step involving hydrolysis had an equilibrium constant of only 4 at the active site of the enzyme (13). The very tight binding affinity (K_d ~ 10^-11 M) of ATP to myosin is used in the cycle to induce a change in enzyme structure that breaks the otherwise tight interaction of myosin with actin in the so-called rigor complex. After dissociation of the myosin-ATP complex from the actin, the hydrolysis of ATP converts the myosin to a myosin-ADP-Pi state that can reassociate weakly with actin. Subsequent conformational changes coupled to the sequential release of Pi and then ADP drive the swinging of a lever arm during force production (18, 19). The key to understanding coupling is to recognize that the myosin motor cycles between tight- and weak-nucleotide-binding states in reactions that are opposed and therefore coupled to cycling between tight- and weak-filament-binding states. The details of this energy transduction cycle are derived from a combination of structural, spectroscopic, equilibrium, and kinetic measurements; transient-state kinetic analysis has played a central role in defining the pathway.

The coupling of ATP hydrolysis to force production by kinesin is different, but it relies on similar principles in that the binding of substrate and release of products are coupled to conformational switching between tight- and weak-filament-binding states (14, 15, 20). Like myosin, cycling between two nucleotide-binding states is coupled to cyclical changes in the affinity of the kinesin motor domain for binding to the microtubule surface. However, the pathway is complicated by the negative cooperativity between the two ATPase domains of the dimeric motor. It is believed that strain induced when simultaneously binding both motor domains to the microtubule surface causes the leading head into a weak-nucleotide-binding state stimulating the release of product, ADP. In contrast, the trailing head binds ATP tightly, and the tight association with the microtubule surface also stimulates ATP hydrolysis. The subsequent release of Pi is then coupled to the dissociation of this trailing head from the microtubule that allows it to leapfrog forward, thereby being converted from the trailing to a leading motor. As this motor domain then binds to the microtubule surface in its new role as leading motor, it reaches a weak-nucleotide-binding state and rapidly releases the bound ADP. Unlike myosin in which one step of the cycle can be attributable to the force-producing step, net displacement of kinesin along the microtubule surface occurs with a complete cycle of the ATPase shown in Fig. 3a, which is rate limited by the release of Pi from the trailing head. This complex pathway was derived by a relatively small set of simple and direct experiments using transient kinetic methods to measure the rate of each reaction and to provide definitive evidence for this alternating site ATPase pathway. For example, Fig. 3b shows the effect of increasing ATP concentrations in stimulating the release of ADP from kinesin bound to a microtubule.

Figure 3. Pathway of the kinesin ATPase. (a) The pathway is shown for the cyclical interaction of kinesin ''heads'' with the microtubule surface driven by the binding and hydrolysis of ATP and release of products. When both heads are bound to the microtubule, then strain leads weak nucleotide binding in the leading head (right-most image). In a key step that leads to an alternative site pathway, ATP binding to the trailing head caused the leading head to bind to the microtubule, which stimulates the release of ADP (steps 1 and 2). The cycle is completed by the hydrolysis of ATP (step 3) and the release of the trailing head from the microtubule coupled to the dissociation of Pi (step 4). (b) Kinetic data to support this model is shown, in which a fluorescent analog of ADP (mant-ADP) was bound to the kinesin, and the kinesin-mantADP complex was mixed with microtubules at various concentrations of ATP. One ADP was released rapidly from only one of the two kinesin heads in the absence of ATP. The binding of ATP to the first head simulates the release of ADP from the second head. These data directly demonstrate the alternating site pathway in which the binding of substrate to one site stimulates product release from the neighboring site. Fitting of this data by simulation of the complete pathway allows definition of the rates of ATP binding and of ADP release. Reproduced with permission from Reference 20.

Transient-Kinetic Tools and Techniques

Transient-kinetic techniques most often rely on the rapid mixing of reactants with enzyme to initiate the reaction. This mixing is essential so that all enzyme molecules start reaction in synchrony with one another; therefore, the time dependence of the observable reactions defines the kinetics of interconversion of enzyme intermediate states. Because mixing requires a finite amount of time, conventional methods are limited in their ability to measure very fast reactions. For example, a typical value for the “dead time” of a stopped-flow instrument is approximately 1 ms, which is because of the time it takes to fill the observation cell. Thus, reactions with a half-life of less than 1 ms (rate > 700 s^-1) are difficult to observe depending on the signal to noise ratio. With a favorable signal to noise ratio, rates on the order of 2000 s^-1 can be measured, but it is rare. Other transient kinetic techniques have been devised to break this time barrier. Both temperature-jump and pressure-jump experiments can approach the 1-μs limit, but both only allow observation of relaxation of a system of reactants from one equilibrium position to another and therefore have less widespread use. Modern microfluidic methods have also achieved mixing times in the microsecond range and offer the promise of more widespread use. In addition, recent efforts have succeeded in combing rapid mixing followed by mass spectrometry analysis to detect enzyme intermediates.

Stopped-flow methods

The two prominent transient-kinetic mixing methods are stopped flow and rapid chemical quench flow. In the stopped flow, the instrument mixes and then forces reactants through a flow cell. After an abrupt stop of the flow, the observation cell contains reactants that were just mixed within the previous millisecond. One can then trigger a computer to collect data to measure changes in optical signals such as absorbance, fluorescence, or light scattering as a function of time after mixing. Other spectroscopic methods such as electron paramagnetic resonance have been employed, but many traces must be collected and averaged to improve the signal to noise ratio. Stopped-flow methods have a distinct advantage in that one can often obtain data of high quality (high signal-to-noise ratio) over a series of concentrations of substrate with a modest investment of time and materials. These data can then accurately define the concentration dependence of observable rates of reaction; this information is critical in developing a model for the enzyme pathway. However, stopped-flow signals are sometimes difficult to interpret uniquely, especially when fluorescence data Scheme multiple exponentials, as described below. An important solution to the problem can be achieved by correlating stopped-flow data with measurements of the chemical conversion of substrate to product using rapid quench-flow methods.

Figure 1b illustrates the analysis of substrate binding and dissociation using stopped-flow fluorescence methods. The concentration dependence of the binding rate defines a two-step sequence that involves a weak rapid-equilibrium binding followed by isomerization to tighter binding. The inset to Fig. 1b shows an experiment to measure the substrate dissociation rate. Combined, the two experiments accurately define the kinetic parameters that govern the two-step binding sequence.

Rapid quench-flow methods

Rapid chemical-quench-flow methods are employed to measure the chemical conversion of substrate to product without necessarily relying on an optical signal. Often, radiolabeled substrates are used, and the substrate and product are resolved chromatographically to allow quantification of the conversion of substrate to product. The reaction is started by mixing the enzyme with substrate and then stopped by mixing with a quenching agent, such as 2N acid or base. In a quench-flow apparatus, reactants are driven through loops of tubing at defined speeds to control the timing and to achieve reaction times as short as 2 ms. Longer reaction times, up to approximately 100 ms, are achieved by using longer loops of tubing. Even longer reaction times, greater than 100 ms, require a push-pause-push mode in which the first push forces the reactants into a reaction loop and after a pause of known duration, a second push forces the reactants to mix with a quenching agent and then out into a collection tube. The method can be time consuming and tedious compared with stopped-flow, but rapid quench flow methods have two distinct advantages. First, they provide a direct measurement for the rate of conversion of substrate to product at the active site; second, they provide a measurement of reaction amplitude in units of concentration that can be directly related to the concentration of enzyme active sites. Accordingly, rapid quench-flow data can be interpreted more easily in evaluating to a given model. In addition, they allow one to assess the extent to which dead enzyme or microheterogeneity in the enzyme and/or substrate might influence interpretation of the data.

Figure 2b shows the results of a rapid-quench single-turnover experiment performed with EPSP synthase with enzyme in excess over the radiolabeled substrate, PEP. The data show the transient formation and decay of the tetrahedral intermediate, which led to its subsequent isolation and structure determination.

When transient kinetic methods fail

Conventional transient-kinetic methods are not always applicable to every enzyme system. In particular, enzymes that have very fast turnover rates such as carbonic anhydrase are not amenable to single-turnover kinetic methods and may require the use of stopped-flow methods just to observe reactions in the steady state. In addition, enzymes with very high K_m values are sometimes difficult to study because the high substrate concentrations needed to saturate the rate of reaction increase the background in attempts to observe product formed at a concentration equal to only one per enzyme site. However, these limitations are being challenged constantly by the development of better instrumentation, new methods, and better signals. If one is lucky or wise enough to choose an enzyme with K_m values in the micromolar range and k_cat less than several hundred per second, then a large range of experiments is possible.

Experimental Design and Interpretation of Data

The overall goal of a comprehensive kinetic study is to provide estimates for each step in the pathway and to identify enzyme-bound intermediates. The time dependence of an enzyme-catalyzed reaction can be rather complex for even a simple reaction sequence that contains only one substrate, one product, and one enzyme-bound intermediate such as the reaction illustrated in Scheme 1. Nonetheless, careful design and rigorous interpretation of a combination of equilibrium and kinetic data can define all eight rate constants under favorable circumstances; in particular, definition of the reverse rate constants usually requires that the reaction be measurable in the reverse direction. In those cases in which rates cannot be defined with certainty, the degree of uncertainty must be stated. For example, in some cases the data may only indicate that k_-2 and k₃, for example, must be greater than 1000 s^-1, but no data define an upper limit. In either case, the data could show that the formation of the intermediate is the kinetically significant step and that the intermediate breaks down at a fast rate. Given the very nature of the reaction, this method may be the best possible and perhaps all that is important mechanistically.

Equilibrium measurements

Steady-state and equilibrium measurements are extremely important to place constraints on the interpretation of more complex kinetic experiments. For example, measurement of the overall equilibrium constant for the reaction defines the product of equilibrium constants for all four steps, K_net = K₁K₂K₃K₄. In addition, it is often possible to measure the two internal equilibria, K₂ and K₃ if concentrations of enzyme can be attained that are higher than the dissociation constants for substrate and product. Finally, dissociation constants for substrates and products can be measured in some instances, particularly with multiple substrate reactions when one of the reactants can be left out to allow the binding but not reaction of the other substrate. Whatever information can be obtained will facilitate the design of subsequent experiments (i.e., what concentrations of substrate are needed to saturate the enzyme) and in their interpretation (i.e., knowing that k₂/k_-2 = K₂ provides an important constraint in globally fitting data).

Binding kinetics

It is useful to approach the solution of an enzyme pathway from both ends and work inward. Measurement of the substrate-binding kinetics is a good first start, but it will depend on a useful signal. Often, changes in protein fluorescence occur that reflect changes in protein structure induced by substrate binding; these signals can be monitored to measure the kinetics of binding and isomerization. In other cases, a fluorescent analog of a substrate or a fluorescently labeled protein can provide a useful signal. In either case, definition of rate constants that govern binding assist in the design and interpretation of subsequent experiments to measure rates of substrate to product conversion at the active site. Figure 1b illustrates the measurement of substrate binding kinetics.

Pre-steady-state burst kinetics

Important results are obtained in an experiment where enzyme is mixed with an excess of substrate and then the formation of product is monitored over the time period of a few enzyme turnovers and with an enzyme concentration high enough to allow quantification of one product per enzyme site. Under conditions in which substrate binding and chemical conversion to product are faster than the release of product, one observes a “burst” of product formation equal to one product per enzyme site, followed by steady-state turnover.

The mere observation of a burst implies that a step after chemistry is at least partially rate limiting for steady-state turnover. In addition, if no observable burst occurs, then the data imply that chemistry is largely rate limiting. When a burst can be observed, quantitative fitting of the amplitude and rate of the burst phase relative to the steady-state phase affords estimates for three rate constants: k₂, k_-2 and k₃ in the pathway shown above (Scheme 2).

Scheme 2.

Single turnover kinetics

If enzyme can be obtained at concentrations approaching the K_d or K_m for substrate, then experiments can be performed with enzyme in excess of substrate. In these experiments, one can observe the net conversion of substrate to intermediate and form product in a single enzyme cycle. The real advantage of the method is in the signal-to-noise (or background) ratio of the data. While in a pre-steady state burst experiment, one might be looking for the appearance of an intermediate in the background of 100-fold higher concentration of substrate; in a single turnover experiment, that same intermediate might appear as 30% of the total substrate. This finding was the case in studies on EPSP synthase, in which single-turnover experiments revealed the presence of the tetrahedral intermediate, which led to its isolation and structure determination (Fig. 2b).

Interpretation of transient kinetic data

Unlike the standard protocols for steady-state kinetic analysis, transient kinetic analysis is dependent on the availability of signals to measure individual steps of the reaction. Moreover, the observable kinetics change and can be complex or deceivingly simple depending on the relative magnitudes of sequential steps in a pathway. The rule of thumb is that one exponential phase exists in the time dependence of a reaction for each step in the pathway. For example, the kinetics of signals observable according to Scheme 2 will follow a triple exponential function: Moreover, it is important to note that the observed rates (λ values) do not translate directly to rate constants for individual steps except in the rare case where each step is irreversible. Rather, the observable rates are a function of all rate constants that are reversibly linked (1, 21, 22). In general, the observed rate approaches the sum of the rate constants for all steps that contribute to the observable transient. A complete discussion of this is beyond the scope of this review, but some simplifying concepts are important to note. For example, if the binding of substrate is a rapid equilibrium or the experiment is conducted at sufficiently high substrate concentration, then the exponential term that governs the formation of ES is so fast that it is dropped from the equation. In addition, in a pre-steady-state burst experiment, the last exponential term is lost because the release of products regenerates free enzyme, which blends the time dependence of the reaction into the steady-state phase. Thus, it is common that for this three-step pathway, the observed rate of formation of product during a pre-steady-state burst experiment follows a single exponential with a rate given by the sum, k_observed = k₂ + k_-2 + k₃ (followed by linear steady-state turnover).

Under some conditions, the kinetics of the reactions simplify, but the validity of such simplifying assumptions is limited. Moreover, as a reaction becomes more complex, the mathematical modeling of the data becomes intractable. For these reasons, methods have been developed for modeling and fitting kinetic data by computer simulation based on numerical integration of the full rate equations without simplification. The data shown in Fig. 3b, for example, can only be analyzed by simulation to obtain meaningful information because of complexities in the experiment. However, in fitting the data by simulation, the rate constant for ATP binding is defined accurately by the observed increase in rate of the slow reaction phase as a function of ATP concentration.

Computer simulation and global data fitting

Kinetic data can be fitted directly to a given model without invoking simplifying assumptions needed to solve mathematical equations. Rather, by numerical integration of the rate equations, complex models can be examined in fitting data over a wide range of concentrations and differing starting conditions. When fitting data by computer simulation, one bypasses mathematical modeling entirely and fits data directly to the model. Moreover, many experiments can be fitted simultaneously to a single unifying model. Several computer programs are currently available including, DynaFit (BioKin, Ltd., Watertown, MA), Copasi (EML Research, Heidelberg, Germany), and KinTek Global Kinetic Explorer (KinTek Corporation, Austin, TX), and all are available on the internet. The major difficulty in using these programs occurs because of the ease with which one can propose overly complex models in attempting to explain kinetic data. Understanding which kinetic constants are actually constrained by the data becomes extremely difficult when fitting multiple parameters to several data sets. KinTek Explorer addresses this problem by allowing the user to scroll a given rate constant, starting concentration, or output factor and watch the curves change in shape. This dynamic simulation immediately reveals whether a given constant has a significant effect on the fit to the data and shows when a model is overly complex.

The future of kinetic analysis lies in the use of these powerful computer simulation methods to design experiments and to fit data rigorously to extract mechanistic information. Ongoing work is directed toward the development of more robust algorithms to address the confidence intervals with which individual parameters can be obtained from modeling a given set of data. With these tools, one can accurately establish a given reaction mechanism and provide estimates for the rates and free-energy changes for each kinetically significant step in the pathway.

References

1. Johnson KA. Transient-state kinetic analysis of enzyme reaction pathways. The Enzymes. 1992; XX:1-61.

2. Johnson KA. Conformational coupling in DNA polymerase fidelity. Annu. Rev. Biochem. 1993; 62:685-713.

3. Patel SS, Wong I, Johnson KA. Pre-steady-state kinetic analysis of processive DNA replication including complete characterization of an exonuclease-deficient mutant. Biochemistry 1991; 30:511-525.

4. Wong I, Patel SS, Johnson KA. An induced-fit kinetic mechanism for DNA replication fidelity: direct measurement by single-turnover kinetics. Biochemistry 1991; 30:526-537.

5. Donlin MJ, Patel SS, Johnson KA. Kinetic partitioning between the exonuclease and polymerase sites in DNA error correction. Biochemistry 1991; 30:538-546.

6. Tsai YC, Johnson KA. A new paradigm for DNA polymerase specificity. Biochemistry 2006; 45:9675-9687.

7. Anderson KS, Sikorski JA, Johnson KA. A tetrahedral intermediate in the EPSP synthase reaction observed by rapid quench kinetics. Biochemistry 1988; 27:7395-7406.

8. Anderson KS, Johnson KA. Kinetic and Structural Analysis of Enzyme Intermediates: Lessons from EPSP Synthase. Chem. Rev. 1990; 90:1131-1149.

9. Anderson KS, Sammons RD, Leo GC, Sikorski JA, Benesi AJ, Johnson KA. Observation by 13C NMR of the EPSP synthase tetrahedral intermediate bound to the enzyme active site. Biochemistry 1990; 29:1460-1465.

10. Lewis J, Johnson KA, Anderson KS. The catalytic mechanism of EPSP synthase revisited. Biochemistry 1999; 38:7372-7379

11. Anderson KS, Johnson KA. “Kinetic competence” of the 5-enolpyruvoylshikimate-3-phosphate synthase tetrahedral intermediate. J. Biol. Chem. 1990; 265:5567-5572.

12. Eisenberg E, Moos C. Actin activation of heavy meromyosin adenosine triphosphatase. Dependence on adenosine triphosphate and actin concentrations. J. Biol. Chem. 1970; 245:2451-2456.

13. Lymn RW, Taylor EW. Mechanism of adenosine triphosphate hydrolysis by actomyosin. Biochemistry. 1971; 10:4617-4624.

14. Gilbert SP, Moyer ML, Johnson KA. Alternating site mechanism of the kinesin ATPase. Biochemistry 1998; 37:792-799.

15. Gilbert SP, Webb MR, Brune M, Johnson KA. Pathway of processive ATP hydrolysis by kinesin. Nature 1995; 373:671-676.

16. Steitz TA. DNA polymerases: structural diversity and common mechanisms. J. Biol. Chem. 1999; 274:17395-17398.

17. Geeves MA, Holmes KC. Structural mechanism of muscle contraction. Annu. Rev. Biochem. 1999; 68:687-728.

18. Geeves MA, Holmes KC. The molecular mechanism of muscle contraction. Adv. Protein Chem. 2005; 71:161-193.

19. Auerbach SD, Johnson KA. Alternating site ATPase pathway of rat conventional kinesin. J. Biol. Chem. 2005; 280:37048-37060.

20. Johnson KA. Rapid kinetic analysis of mechanochemical adeno-sinetriphosphatases. Methods Enzymol. 1986; 134:677-705.

21. Johnson KA. Rapid quench kinetic analysis of polymerases, adenosinetriphosphatases, and enzyme intermediates. Methods Enzymol. 1995; 249:38-61.

22. Doublie S, Tabor S, Long AM, Richardson CC, Ellenberger T. Crystal structure of a bacteriophage T7 DNA replication complex at 2.2 A resolution. Nature 1998; 391:251-258.

Further Reading

Johnson KA, ed. Kinetic Analysis of Macromolecules. 2003. Oxford University Press, Oxford, UK.

Gutfreund H. Kinetics for the Life Sciences: Receptors, Transmitters and Catalysts. 2002. Cambridge University Press, Cambridge, UK.

See Also

Enzyme Kinetics

Enzyme Catalysis: Roles of Structural Dynamics in

Techniques to Study Enzyme Kinetics

DNA Replication: An Overview