CHEMICAL BIOLOGY
Electron Transfer, Chemical Roles of Water in
Ilya A. Balabin and David N. Beratan, Duke University, Durham, North Carolina
Spiros S. Skourtis University of Cyprus, Nicosia, Cyprus
doi: 10.1002/9780470048672.wecb148
Water plays multiple roles in biological electron transfer (ET): energy bath, polarizable medium that defines the reaction coordinate, electronic coupling bridge, and intimate participant in molecular recognition. This article explores these many faces of water in ET. Links are drawn to reactions in photosynthesis, oxidative phosphorylation, proton-coupled ET, and DNA damage and repair.
Biological electron transfer (ET) reactions are ubiquitous in nature. They define the fundamental reactions of bioenergetics, biocatalysis, and nucleic acid synthesis and repair. These reactions occur both in membranes and in aqueous environments. In both settings, water plays multiple roles in the ET reaction kinetics and dynamics (1-5). The roles of water are diverse. Its roles vary from establishing a high dielectric screening medium to supporting the solvation of counterions to establishing hydrogen-bonded relays to providing electron tunneling pathways and proton wires for key transport reactions. Our aim is to review the influence of water on biological ET and, as such, examine some of the many roles of water in these reactions.
Biological Background: The Many Roles of Water in Biology
Water is present in protein cavities as individual molecules, water chains, and clusters. Indeed, tightly bound waters can be resolved in X-ray crystallography experiments. Water molecules in larger cavities, especially those with a hydrophobic surface, are mobile and less readily resolved. In some proteins, such as the cytochrome b6f complex or cytochrome c oxidase, bound water molecules tend to form water chains. These water molecules provide hydrogen-bonded relays for proton transfer, and they may mediate donor-to-acceptor electronic coupling (2-6).
ET reactions define the early elementary steps of bioenergetics (2-5). These reactions capture energy from sunlight via photosynthesis in plants and transduce energy through oxidative phosphorylation in animals (2). ET reactions also drive much of biocatalysis and DNA damage repair (2-5, 7). In biological ET, an electron moves from one spatially localized chemical group (the electronic donor) to another (the electronic acceptor). Typical donor and acceptor groups are hemes, chlorins, iron-sulfur clusters, blue-copper centers, quinones, and flavins, although small-molecule redox mediators are important as well (2-5). Donor and acceptor groups may be located within the same protein assembly, as in the photosynthetic reaction center, or in different proteins. Biological ET reactions typically occur over distances beyond van der Waals contact, where the direct donor-to-acceptor electronic interaction is negligible. As such, these rates depend on the strengths of this electronic coupling and on the (nuclear) activation free energy. In contrast to small-molecule chemistry, the structure of the intervening protein, nucleic acid, or solvent medium is expected to have a profound effect on reaction kinetics (1-5). Water influences both the electronic coupling and the activation free energy of ET reactions.
Chemical Roles of Water in Biomolecular ET
The last 50 years have witnessed the establishment of a truly molecular-level description of electron transfer chemistry. From the Marcus description of how solvent polarization defines the ET reaction coordinate, to fully quantum treatments that describe electron and nuclear tunneling contributions to the kinetics, to atomistic simulations of reaction coordinate motion, a comprehensive view of biological ET is emerging (1-5).
Inner-and outer-sphere ET
Electron transfer reactions are categorized as outer or inner sphere. In outer-sphere processes, structural changes during ET largely involve solvent reorientation (polarization). Inner-sphere reactions involve changes in the bonding to the redox unit and are more difficult to describe using the ET theory as it is explained here.
Outer-sphere biological redox reactions occur between cofactors beyond van der Waals contact distances, and they occur mostly via electron tunneling. The ET rate is proportional to the product of an electron tunneling probability and an Arrhenius-like activation factor (1-5). The electron tunneling probability is proportional to the square of the donor-acceptor electronic coupling, and the Arrhenius-like factor is given by exp[-∆G*/KBT], where ∆G* is the activation free energy, KB is Boltzmann’s constant, and T is the temperature. The activation factor arises from changes in nuclear polarization coupled to the electron transfer event.
The activation free energy ∆G * is defined by two terms. One term is the reaction free energy [∆G(0)], which is derived from the redox potential difference of the donor and acceptor. The second term is the medium reorganization energy (λ), which is the energy stored in the solvent inertial degrees of freedom when the electron is shifted suddenly from donor to acceptor (1-5). Marcus theory predicts the activation free energy:
![]()
Because ∆G * enters the rate expression in the argument of an exponential, changes in driving forces and reorganization energies sweep ET rates over many orders of magnitude. In photoinduced electron-transfer reactions (as in the photosynthetic reaction center and photolyase (2, 7), the thermodynamic driving force for charge separation and charge recombination reactions are very different. Indeed, this difference is believed to enhance the efficiency of photosynthetic charge separation (1).
The reorganization energy λ in Equation 1 has contributions from “inner-sphere” and from “outer-sphere” (i.e., solvent) motion. The outer-sphere reorganization energy (λout) often dominates the activation free energy. The activation free energy for ET depends on the match between —∆G(0) and k. That is, the reaction rate is maximized (for a fixed donor-acceptor distance) when —∆G(0) = λ. In the regime where —∆G(0) < λ, the “normal” regime, the reaction rate increases with increasing thermodynamic driving force. When —∆G(0) > λ, the reaction is “inverted,” and its rate slows with additional increases in driving force. A great achievement of the 1980s was to access both of these regimes (1, 3), which validated the most dramatic prediction of the Marcus theory. Polar solvents like water have larger kout than nonpolar solvents (kout for water is typically a few electron volts and for nonpolar solvents is typically tenths of electron volts). Therefore, the inverted regime of ET in aqueous solvent is accessed at larger driving forces than ET in low-polarity solvents, and aqueous ET reactions are more likely to be in the “normal” regime. As such, docking or association processes that exclude water would decrease kout and accelerate the kinetics. This simple observation explains a possible advantage for carrying out the charge separation reactions of bioenergetics in nonpolar transmembrane proteins rather than in aqueous media. Membranes also play a second and important role by defining a simple directionality for electron and proton transport.
Inner-sphere ET reactions are of great interest in chemistry and biology (8). However, the kinetics of these reactions are rather complex as they involve bond breakage and formation with the redox group. For inner-sphere processes, electron transfer need not be rate limiting and the reaction coordinate may not be determined as described above for pure ET events. ET kinetics may also be gated by conformational changes or ion motion (9, 10).
When inner-sphere motion is coupled to ET but does not control the reaction mechanism, it adds to the outer-sphere reorganization energy to define a total λ value for Equation 1. Changes in bond lengths and vibrational frequencies contribute to the reorganization energy and are known as inner-sphere components. Inner-sphere reorganization energies routinely are computed with quantum chemical methods and are typically on the scale of tenths of electron volts; outer-sphere reorganization energies can be larger than this size and frequently are computed using continuum dielectric methods (20).
In addition to bulk water, which contributes to λout, buried water molecules can make significant contributions to the overall reorganization energy of biological ET reactions. The magnitude of the buried-water contribution depends on the location of the waters relative to the D and A moieties and on their number. Finite-difference Poisson-Boltzmann calculations for the R. viridis photosynthetic reaction center, which contains more than 100 buried waters, show that the buried-water contribution to the total reorganization energy varies from 0.05 to 0.27 eV for different PRC ET reactions (Reference 11 and references therein). The largest contribution (0.27 eV) is for the cytochrome to the special pair ET reaction and constitutes 25% of the total computed reorganization energy (total meaning bulk and buried water, protein, and membrane). The effect of water on ∆G(0) strongly depends on the ET system considered, for example, on how deeply the D and A moieties are buried inside the protein (which screens the bulk solvent) and on the positions of internal waters relative to the D and A molecules.
Water-mediated molecular interactions
Water has C2v symmetry. In the gas phase, the measured O-H bonds are 0.957 A, and the H-O-H angle is 104.5° (12). Liquid water and ice have structures controlled by the formation of hydrogen bonds. These bonds make it possible for hydrogen ions to exchange among water molecules on the millisecond to picosecond time scale (13), depending on pH. The extensive and dynamic hydrogen bond networks account for many unusual properties of water and hydrated biomolecules (12).
Water-mediated molecular interactions, including hydrogen bonding, hydrophobic effects, ion pairing, and cation-π interactions, play a central role in biomolecular structure and function (5). In soluble proteins, most nonpolar residues that cannot form hydrogen bonds with water are located in the protein core, whereas polar and charged residues form most of the protein surface, which increases the protein-solvent stability (14). Cation-π interactions, which involve electrostatic attraction between a cation and the negative electrostatic potential associated with the face of a π system, influence both the protein structure and the ion distribution in solvent (5). These factors play a central role in protein-protein and protein-ligand binding, particularly influencing the structure of the thin water layers between biomolecules in an encounter complex and thereby influencing intermolecular ET reactions (15).
Water and nonequilibrium solvation
Water also influences the nature of the motion along the ET reaction coordinate (donor, acceptor, and solvent degrees of freedom that are coupled to ET). A measure of the short timescale nonequilibrium solvation dynamics is the Franck-Condon time τFC. This time is the time it takes for the ET system to move away from the crossing point of the electron donor and acceptor potential surfaces where the activation complex is formed. For temperature T and reorganization energy λ, tFC is τFC ![]() where
where ![]() is the root mean square fluctuation in the donor to acceptor energy gap (16) and references therein). For biological ET, TFC was computed for azurin ET (Ru2+/Ru3+) (17) using a semiclassical molecular dynamics (MD) methodology (18). The computedTFC was 2.4 f sec with significant protein and solvent (water) contributions. For protein alone, it was TFC ≈ 4.1 f sec, and from solvent alone, it was TFC ≈ 3.0 f sec. Water solvation dynamics are equally important for excited-state ET, in which the formation of the D excited state by photoexcitation may induce a large dipole moment change of the D moiety that is followed by rapid protein matrix and solvent response. Excited-state ET from (FADH-)* to DNA in DNA photolyase is an example of an ET reaction in which the change in dipole moment of the D moiety induced by photoexcitation [(FADH- →(FADH-)*] is large because of a pi to pi* charge transfer transition of the flavin ring (19). Experimental measurements of the solvation dynamics of (FADH-)* in DNA photolyase have shown very fast and significant solvation dynamics induced by photoexcitation with relaxation timescales ranging from 2 to 60 picoseconds (20). This solvation dynamics, which is much faster than the ET rate, is partially attributed to trapped water molecules in the DNA photolyase active site (20). Solvent relaxation can limit rates that are fast compared with the solvent relaxation timescale (3). Bulk water is characterized by a broad distribution of relaxation timescales (subpicosecond and slower) and may therefore act as a rate-limiting solvent for ET reactions (21).
is the root mean square fluctuation in the donor to acceptor energy gap (16) and references therein). For biological ET, TFC was computed for azurin ET (Ru2+/Ru3+) (17) using a semiclassical molecular dynamics (MD) methodology (18). The computedTFC was 2.4 f sec with significant protein and solvent (water) contributions. For protein alone, it was TFC ≈ 4.1 f sec, and from solvent alone, it was TFC ≈ 3.0 f sec. Water solvation dynamics are equally important for excited-state ET, in which the formation of the D excited state by photoexcitation may induce a large dipole moment change of the D moiety that is followed by rapid protein matrix and solvent response. Excited-state ET from (FADH-)* to DNA in DNA photolyase is an example of an ET reaction in which the change in dipole moment of the D moiety induced by photoexcitation [(FADH- →(FADH-)*] is large because of a pi to pi* charge transfer transition of the flavin ring (19). Experimental measurements of the solvation dynamics of (FADH-)* in DNA photolyase have shown very fast and significant solvation dynamics induced by photoexcitation with relaxation timescales ranging from 2 to 60 picoseconds (20). This solvation dynamics, which is much faster than the ET rate, is partially attributed to trapped water molecules in the DNA photolyase active site (20). Solvent relaxation can limit rates that are fast compared with the solvent relaxation timescale (3). Bulk water is characterized by a broad distribution of relaxation timescales (subpicosecond and slower) and may therefore act as a rate-limiting solvent for ET reactions (21).
Tunneling mediation
The tunneling characteristics of biological ET have placed considerable recent focus on protein and solvent (3, 22). The energetic proximity of solvent and protein orbitals to the redox active states of the donor and acceptor cofactors provides superexchange pathways for tunneling (23). That is, the energy cost of tunneling via these protein states is much lower than the cost of tunneling through “pure” empty space. As such, the intervening medium facilitates weak tunneling propagation of the electron from donor to acceptor via coupling pathways (24). The tunneling probability through this medium multiplies the Marcus factor described above. Early models for protein-electron tunneling predicted that rates would drop by about a factor of 10 for each 1.6 A. In the 1980s and 1990s, approaches were introduced to explore the influence of the specific medium structure on the tunneling. In recent years, the influence of medium dynamics was added to complete the models (16, 25-29, and references therein).
The role of disordered water as a tunneling medium has been the subject of several electronic-structure computational studies. Early calculations focused on the Fe(H2O)6+3/+2 self exchange reaction (30-32). These calculations concluded that disordered water is not a very effective electron-tunneling medium. More recently, one-electron pseudopotential analysis of electron tunneling through water layers placed between electrodes indicated that water is a modest tunneling mediator (33). Another computational study of aqueous ET between ion pairs used MD simulations with INDO/S and CASSCF calculations of the electronic coupling (34). This study showed that water can be an essential tunneling medium. The computed INDO/S tunneling matrix element decay parameter was 2.0 A-1and the ab initio values ranged from 1.5 to 1.8 A-1. Experiments in aqueous glasses give average decay of 1.68 A-1 (22).
Of particular interest is how oriented water in confined spaces contributes to tunneling. Several experiments indicate a special role for bridging waters (22, 35-37). Recent studies of interprotein ET reveal details of how the ensemble of docked structures contributes to the observed rate. The “dynamic docking” paradigm for ET between weakly associated proteins suggests that minority population configurations dominate the electron tunneling mediation (38). It seems likely that water can contribute to dynamic docking by influencing donor-acceptor coupling pathways or by modifying the reorganization energies as the proteins approach a docked structure. Newly developed experimental methods enable the study of electron transfer kinetics between cocrystallized proteins. These experiments are likely to provide direct answers to some of the questions of how specific waters at protein-protein interfaces may influence ET kinetics (22, 39).
The fleeting nature of water structures in proteins makes it extremely challenging to study their influence on ET by direct means. Indications that a few key bridging waters seem to accelerate protein ET reactions motivated a theoretical simulation of interprotein ET in the presence of explicit bridging water molecules (35-37). Pathway studies indicated that waters between cytochrome c2 and the photosynthetic reaction center serve as key mediators (Fig. 1) (40) Quantum studies of water mediation in protein-protein systems indicate that spatially confined waters between proteins may enhance electronic coupling in a regime just beyond protein-protein contact (Fig. 2) (41). In this regime, the distance permits entry of a few intervening waters and the coupling is enhanced by constructive interference among multiple coupling pathways. At larger distances, the effect rapidly dissipates. These studies are motivating small-molecule studies of water-mediated electron transfer in systems with well-defined cavities that may bind water molecules (D. Waldeck, private communication).
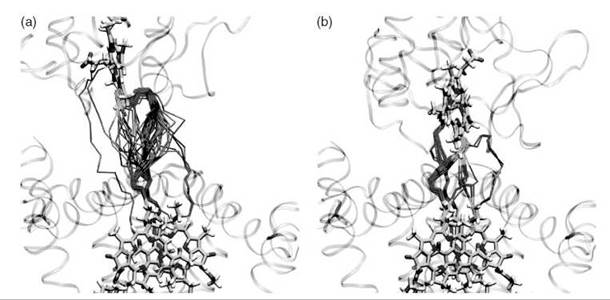
Figure 1. Water-mediated ET pathways between cytochrome c2 and the photosynthetic reaction center in an encounter complex (left panel) and the more fully docked state (right panel) (40). The pathways are shown for 50 conformations obtained by MD sampling. Cofactor-mediated pathway fragments are shown in green, protein-mediated fragments are shown in purple, and water-mediated fragments are shown in orange.

Figure 2. Dependence of the mean square electronic coupling on distance between two porphyrin rings in the cytochrome b5 self-exchange ET reaction (41). For each distance, system conformations were sampled using MD and the coupling was computed for each conformation at the extended Huckel level. The black line marked XH(P, W) shows the water-mediated coupling; for comparison, the red line marked XH(P) shows the coupling computed for the same protein conformation in vacuum. Conformational snapshots typical for the three coupling regimes are shown.
Proton-coupled ET reactions
In bioenergetics, electron transfer drives proton transfer; proton gradients in turn power ATP synthesis. In addition to coupling to medium polarization, biological ET reactions may also couple strongly to proton transfer. As such, rates may be limited by proton transfer or electron transfer or may fall into an intermediate regime. Rapid advances are being made in both the theoretical and experimental investigation of these coupled rate processes (42, 43, and references therein).
Isotope effects on ET reactions
Substitution of H2O solvent by D2O generally leads to a change in ET kinetics (44, 45, and references therein). In the simplest model of ET coupled to a single solvent vibration involving H, substitution of H by D lowers the frequency of the vibration and increases the localization of the vibrational wave functions. These changes influence the Franck-Condon factor for the ET reaction in a way that depends on the temperature and on reaction energetics. For example, at low temperatures, when the vibrations are in their ground states, the increased localization (for deuteration) of the vibrational wave functions is expected to speed up an activationless reaction by enhancing the probability of being at the crossing point between D and A potential energy surfaces. In contrast, for an activated ET reaction at low temperature, the increased localization will reduce the probability of reaching the crossing point by nuclear tunneling, which, thus, slows down the ET reaction.
Protein ET systems have large and somewhat flexible macromolecule assemblies with folded structure and motion strongly coupled to the surrounding solvent. In these systems, isotopic substitution of the solvent may affect multiple factors that influence the ET rate, and, generally, the overall isotope effect on the ET rate is system-dependent. For example, D2O changes protein solvation because the solvent-solvent hydrogen bonds are stronger in D2O compared with H2O, which leads, therefore, to an increased hydrophobic effect. Changes in the fold and volume of a protein may alter the donor-acceptor distance, the redox potentials, and the tunneling-pathway networks, which all influence the ET rate.
The strengthened hydrogen bond networks in D2O, which lower molecular and solvent flexibility, produce larger reorganization energies and affect nuclear fluctuation timescales, which are especially important in gated and solvent-controlled ET. For proton-coupled ET reactions, D2O solvent substitution changes the proton transfer-electron transfer equilibria and kinetics. The literature on the isotope effect on ET is large and growing (44, 45, and references therein).
ET reactions controlled by conformational transitions and solvent viscocity
Because of the rapid decay of the electronic coupling with distance, very long-distance (>40 A) ET reactions rarely occur in a single step. Instead, extremely long range ET involves an array of multiple redox centers, mobile electron carriers, or large-scale motion of redox-active domains (46). All intermolecular ET reactions require either protein-protein docking or formation of an encounter complex in which the two protein cofactors are within a few angstroms (40, 41). In these cases, protein diffusion in solvent, influenced by solvent viscosity, pH, and other factors, can be rate limiting if the formation of an encounter complex is slower than the ET reaction itself.
In unimolecular ET, the rate can be controlled by large-scale cofactor motion, such as the quinone motion in the photosynthetic reaction centers, the Rieske subunit motion in the cytochrome bc1complex (47), or the cytochrome b5-domain in sulfite oxidase. Theoretical models for conformationally controlled ET reactions have been suggested by Hoffman and Rat- ner (48) and Brunschwig and Sutin (49). Large-scale protein or domain motions are themselves linked to the movement of water molecules.
Experimental and Theoretical Methods
Experimental methods
Ultrafast ET reaction kinetics usually is measured using transient absorption or luminescence spectroscopy. ET reactions are initiated by exciting the native or modified ET cofactor or by injecting an electron or hole by a flash-quench technique (22). Slower ET reactions can be studied by using a variety of methods, including calorimetry, stopped flow, dipole relaxation, redox titration, and other techniques (4). Recent experiments on the structural relaxation of water provide intriguing observations of its structure and dynamics. For example, the coexistence of ordered surface water and crystallite-like ice structures following exposure to a femtosecond-range infrared laser pulse was observed with ultrafast electron diffraction methods (50). Studies of the first hydration shell of a water molecule in liquid water using X-ray absorption spectroscopy and X-ray Raman scattering reveal that water molecules typically form only two hydrogen bonds (one donor and one acceptor bond), contrary to predictions of MD simulations that suggest three or four hydrogen bonds (51). Analysis of K-edge X-ray absorption experiments provides an estimate of 1.5 ± 0.5kcal/mol for the average thermal energy required to effect an observable rearrangement between the fully coordinated (“ice-like”) and distorted (“broken-donor”) local hydrogen-bonding configurations (52). Although many questions regarding water structure and dynamics remain open, experimental probes of water are rapidly advancing our understanding (see Reference 53 and references therein).
Theoretical methods
Theoretical approaches to calculating the electronic coupling in proteins and DNA have significantly evolved in the past 20 years (3, and references therein). Early simple models treat proteins as structureless one-dimensional tunneling media, resulting in an electronic coupling decay exponential in distance. The Pathways model (24) quantifies effects of the protein fold. This model uses the fact that tunneling through bonds has a lower barrier associated with it than tunneling through space. Pathways calculations find the optimal combination of bonded and non-bonded links from the donor to the acceptor cofactors using an X-ray-determined protein structure (24). Intriguingly, with essentially one parameter (the ratio of through bond to through space coupling decay), the Pathways model qualitatively described the nature of ET rates in several redox proteins, facilitating an early phase of mapping structural effects on protein ET reactions (24). Semiempirical Schrodinger equation-based methods, such as commonly used extended Huckel-level calculations (25, 54, 55), incorporate the explicit effects of multiple coupling pathway interferences, albeit also in an approximate way. Although ab initio methods have a potential to provide more accurate descriptions, they incur high computational costs given the requirement for extensive geometry sampling in ET reaction simulations (16, 19).
Theoretical methods for estimating the reorganization energy have to account for its large variations in different environments. The Marcus model for λout assumes spherical donors and acceptor moieties embedded in a dielectric continuum that represents the solvent. λout is proportional to (1/εop — 1/εs), where εop is the optical dielectric constant and εs is the static dielectric constant of the medium. The dependence of λout on εs and εop explains why λout is higher in water and highly polar solvents compared with nonpolar solvents. In low dielectric media like membranes, εs and εop are nearly matched, thus lowering the reorganization energy. The simple continuum model cannot be used to compute accurate reorganization energies in complex molecular environments. More sophisticated numerical approaches have been developed for the computation of \ (e.g., References 11, 56, 57, and references therein). Numerical approaches permit the computation of reorganization energies for cofactors of arbitrary shape (e.g., Reference 4). They can also be combined with MD simulations to compute the reorganization energy for different MD conformations of the ET system to assess the influence of fluctuations. Different methods have also been developed for computing ∆G(0) (e.g., References 11, 56, and references therein).
A variety of theoretical descriptions of hydrogen-bonding water networks has been proposed, include flickering clusters, percolation networks, fluctuating charges, random networks, continuum models, and so forth. (58), yet many structural aspects of liquid water remain open to debate (59, 60). Since the first explicit (atomistic) model for water was proposed by Bernal and Fowler in 1933, a variety of water potential functions (force fields) have been developed (61, 62). These water potential functions typically include noncovalent interactions, for example, Coulombic interactions among partial charges assigned to each atom (and to each electron lone pair in some models) and van der Waals interactions among atoms. Some force fields include elastic terms, namely O-H bond stretching and H-O-H angle deformations. Two force fields common in biomolecular simulations are the SPC model and the TIP3 model (61, 62). Both force fields are rigid, three-site descriptions that were parameterized to reproduce the bulk liquid water phase structure and thermodynamics. However, none of these (and similar) force fields accurately predicts the temperature dependence of liquid water’s density (60). Later force fields incorporated intramolecular flexibility [e.g., the F3 C model (62)]. Other improvements include adding fourth and fifth sites, polarizability, and quantum effects (62). Although models like TIP4P and TIP5P provide a more accurate description of homogeneous bulk water, they perform poorly in describing gas-phase clusters and nonpolar solutes in polar solvents (62). In biomolecular simulations, these models cannot correctly account for situations when a nonpolarizable moiety is exposed to different electrostatic environments, either within a static structure or during simulations. Another problem with nonpolarizable models is that of including the average bulk polarization in the potentials. Whereas polarizable force fields, such as the fluctuating charge and related models, attempt to address these problems with varying success, SPC and TIP3P remain the most appropriate force fields for simulations of large biomolecular systems (61).
Sampling of the biomolecular conformations is usually performed using MD simulations or Monte Carlo methods (61, 62). The protonation state of titrateable amino acids can be treated with constant pH dynamics, QM/MM calculations, or continuum electrostatics methods (61, 62). Formation of a protein- protein encounter complex is often studied using Brownian dynamics (63). Studies of protein-protein docking involve electrostatic potential analysis and, more recently, protein flexibility models, for example normal mode analysis (64).
Frontiers in Biomolecular ET Reactions
Protein-mediated ET reactions
The photosynthetic cytochrome b6f complex is an integral part of the oxygenic photosynthetic electron-proton transport chain. It transfers electrons from photosystem II to photosystem I and moves two protons per electron transferred across the photosynthetic membrane to build a transmembrane proton gradient. The solution of the crystal structure of the cytochrome b6f complex (65) revealed the relative positions of its redox-active subunits, cytochrome f, cytochrome b, and the Rieske 2Fe-2S protein, as well as the structural similarities with the respiratory cytochrome bc1 complex. In the cytochrome b6f complex, a lipid-soluble quinol transfers an electron to the Fe2S2 center of the Rieske protein, an electron to the heme bp of cytochrome b6, and two protons to the aqueous side of the thylakoid membrane. The Rieske 2Fe-2S protein subsequently reduces the heme c center of cytochrome f that extends into the aqueous side of the membrane. Cytochrome f reduces the Cu center of water-soluble plastocyanin that in turn transfers the electron to photosystem I. Cytochrome f contains a buried chain of five water molecules inside its heme-binding large domain. The waters are hydrogen bonded to surrounding residues that are highly conserved in cytochrome f sequences (66). It was shown that mutations that affect this water chain impair electron transfer and photosynthetic function (67). The mutations also affected the redox potentials of cytochrome f (Fig. 3).
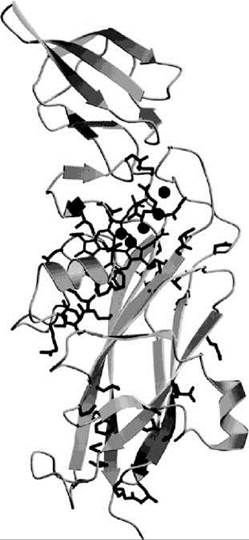
Figure 3. Ribbon diagram of cytochrome f from P. laminosum (66). The heme cofactor is shown as sticks, and the five water molecules that form a chain are shown as spheres. Conserved protein residues cluster around the heme, the water molecules, and the C-terminal connection to the transmembrane helix to form a proton translocation pathway.
It is possible that the water chain interacts with the Rieske 2Fe-2 S protein when the latter approaches the hydrophobic edge of cytochrome f to transfer an electron to the heme (67). Water chains (as long as 10-12 water molecules) and smaller water clusters are also present in bacterial photosynthetic reaction centers. They connect the secondary quinone to the cytoplasmic surface and are thought to participate in proton transfer from the cytoplasm to the secondary quinone (6, and references therein; Fig. 4). Water molecules seem to play a more complex role in cytochrome c oxidase, the terminal component of the mitochondrial and to other bacterial respiratory chains. The protein performs the four-electron reduction of O2 to water and couples it to transmembrane proton transport. The mechanism of function for this enzyme is not fully understood and is the subject of ongoing studies (6, and references therein; Fig. 1). Apart from the role of the water molecules as proton wires, it has also been suggested (although not demonstrated experimentally) that internal waters are involved in redox-linked switching of the proton wires. Electron transfer from the heme a of cytochrome c oxidase to the binuclear CuB-heme a3 site may invert the local electric field between the redox sites and thus cause restructuring of internal waters and the switching of the proton pathways (6, and references therein).

Figure 4. Proton transfer pathway in the photosynthetic reaction center from Rhodobacter sphaeroides connects the solvent-exposed part of the protein (His126 — His128) to the secondary quinone binding site QB (6).
DNA-mediated ET reactions
DNA is a polyelectrolyte with a tightly bound spine of water. Both DNA damage and repair mechanisms involve ET (10). Water is an important determinant of DNA structural stability, both in the form of organized water that occupies the major and minor grooves of the DNA double strand and as bulk solvent (10).
The mechanism of DNA-mediated ET remains poorly understood. Theoretical and experimental studies are consistent with a mechanism of superexchange (tunneling) mediation at short distances and multistep hopping at longer distances. Intensive investigations are exploring the degree of delocalization of “holes” in the DNA stack and the polaronic nature of the transport (10). Water may influence DNA charge transport in a variety of ways. Bulk and structured water around DNA and structural distortions of the DNA molecule itself induce the localization of DNA holes to form polarons. The spatial extent of these polarons has been a subject of debate, and predictions of the polaron size in solvated DNA range from 4-5 adjacent base pairs to 2-3 adjacent GC pairs to a single GC base pair (10). In all cases, solvation reduces the size of the polaron as compared with dry DNA because it stabilizes localized charges. The motion of water and counterions surrounding DNA rather than intramolecular motions of DNA can also determine the timescale of the activation dynamics for the polaron hopping transition (10). Water may also react with DNA holes on guanine bases, and such reactions compete with hole transport (68). Recent neutron diffraction experiments on hydrated DNA decamer duplexes determined the hydrogen and deuterium atomic positions of the water molecules that hydrate the DNA (69). These experiments show that the water network in the DNA minor groove can form interstrand and intrastrand bridges that connect different parts of the duplex by hydrogen bonds. Density functional electronic structure calculations using the hydrated duplex structure identified in these experiments, showed that the structure has three nearly degenerate highest occupied molecular orbitals, each spatially distributed over the G bases, and specific water molecules in the minor groove (70). These results suggest that hydrating water molecules in DNA not only influences the electronic structure of the polaron hole (10) but also may mediate hole transfer by acting as a superexchange bridge (Fig. 4).
Conclusions
A unified view of how water influences biological ET is yet to emerge. Many qualitative effects are apparent: Water produces large reorganization energies, and structured water may produce favorable electron and proton transport pathways. Water at protein-protein interfaces can perturb docking energetics and influence both the coupling mechanisms and ET reaction coordinate. Structured water chains provoke intriguing questions regarding electron and ion communication, coupling, and switching. In nucleic acids, water and DNA counter ions influence both the structure of “holes” and the kinetics of their transport.
References
1. Marcus RA, Sutin N. Electron transfers in chemistry and biology, Biochim. Biophys. Acta 1985; 811:265-322.
2. Cramer WA, Knaff DB. Bioenergetics: energy transduction in biological membranes. 1991. Springer-Verlag, Berlin.
3. Electron transfer-from isolated molecules to biomolecules, pts 1. & II Adv. Chem. Phys. 1999; 106.
4. Balzani V. Electron transfer in chemistry. 2001. Weinheim; New York.
5. Bertini I. et al. Biological inorganic chemistry: structure and reactivity. 2007. University Science Books, Sausalito, California.
6. Helms V. Protein dynamics tightly connected to the dynamics of surrounding and internal water molecules. Chem. Phys. Chem. 2007; 8:23-33.
7. Sancar A. Structure and function of DNA photolyase and cryptochrome blue-light photoreceptors. Chem. Rev. 2003; 103:2203-2237.
8. Taube H. Electron transfer of complex ions in solutions. 1970. Academic Press, New York.
9. Davidson VL. What controls the rates of interprotein electron transfer reactions. Acc. Chem. Res. 2000; 33:87-93.
10. Schuster GB, ed. Long-range charge transfer in DNA. 2004. Springer, Berlin, New York.
11. Sharp KA, Honig B. Electrostatic interactions in Macromolecules: Theory and Applications. Annu. Rev. Biophys. Biophys. Chem. 1990; 19:301-332.
12. Franks F, ed. Water: A comprehensive treatise. Vol 1. 1972. Plenum Press, New York.
13. Xenides D, Randolf BR, Rode BR. Hydrogen bonding in liquid water: An ab initio QM/MM MD simulation study. J. Mol. Liquids 2006; 123:61-67.
14. Nemethy G, Scheraga HA The structure of water and hydrophobic bonding in proteins. III. The thermodynamics properties of hydrophobic bonds in proteins. J. Phys. Chem. 1962; 66:1773-1789.
15. Israelachvili J, Wennerstrom H. Role of hydration and water structure in biological and colloidal interfaces. Nature 1996; 379:219-225.
16. Skourtis SS, Balabin IA, Kawatsu T, Beratan DN. Protein dynamics and electron transfer: Electronic decoherence and non-Condon effects. Proc. Natl. Acad. Sci. USA. 2005; 102:3552-3557.
17. Lockwood DM, Cheng YK, Rossky PJ. Electronic decoherence for electron transfer in blue copper proteins. Chem. Phys. Lett. 2001; 345:159-165.
18. Neria E, Nitzan A. Semiclassical evaluation of nonadiabatic rates in condensed phases. J. Chem. Phys. 1993; 99:1109-1123.
19. Prytkova TR, Beratan DN, Skourtis SS. Photoselected electron transfer pathways in DNA photolyase. Proc. NAtl. Acad. Sci. U.S.A. 2007; 104:802-807.
20. Kao YT, Saxena C, Wang L, Sancar A, Zhong D. Direct observation of thymine dimer repair in DNA by photolyase. Proc. Natl. Acad. Sci. U.S.A. 2005; 102:16128-16132.
21. Zusman LD, The theory of transitions between electronic states - application ot radiationless transitions in polar solvents, Chem. Phys. 1983; 80:29-43.
22. Gray HB, Winkler Jr, Electron tunneling through proteins. Quarter. Rev. Biophys. 2003; 36:341-372.
23. Beratan DN, Onuchic JN, Hopfield JJ. Electron-tunneling through covalent and noncovalent pathways in proteins. J. Chem. Phys. 1987; 86:4488-4498.
24. Beratan DN, Betts JN, Onuchic JN. Protein electron transfer rates set by the bridging secondary and tertiary structure. Science 1991; 252:1285-1288.
25. Daizadeh I, Medvedev ES, Stuchebrukhov AA. Effect of protein dynamics on biological electron transfer. Proc. Natl. Acad. Sci. U.S.A. 1997; 94:3703-3708.
26. Stuchebrukhov A. Long-distance electron tunneling in proteins. Theor. Chem. Acc. 2003; 110:291-306.
27. Xie Q, Archontis G, Skourtis SS. Protein electron transfer: A numerical study of tunneling through fluctuating bridges. Chem. Phys. Lett. 1999; 312:237-246.
28. Balabin IA, Onuchic JN. Dynamically controlled protein tunneling paths in photosynthetic reaction centers. Science 2000; 290:114- 117.
29. Teklos A, Skourtis SS. Electron transfer through time-dependent bridges: differences between Franck-Condon and Born-Oppenheimer breakdown. Chem. Phys. 2005; 319:52-68.
30. Tembe BL, Friedman HL, Newton MD. The theory of the Fe2+-Fe3+ electron exchange in water. J. Chem. Phys. 1982; 76:1490-1507.
31. Larsson S. Electron-exchange reaction in aqueous solution. J. Phys. Chem. 1984; 88:1321-1323.
32. Marchi M, Chandler D. Path-integral calculation of the tunnel splitting in aqueous ferrous-ferric electron transfer. J. Chem. Phys. 1991; 95:889-894.
33. Benjamin I, Evans D, Nitzan A. Electron tunneling through water layers: Effect of layer structure and thickness. J. Chem. Phys. 1997; 106:6647-6654.
34. Miller NE, Wander MC, Cave RJ. A theoretical study of the electronic coupling element for electron transfer in water. J. Phys. Chem. A. 1999; 76:1084-1093.
35. Blankenship RE. It takes two to tango. Nat. Struct. Biol. 2001; 8:94-95.
36. van Amsterdam IMC Ubbink M, Einsle O, Messerschmidt A, Merli A, Cavazzini D, Rossi GL, Canters GW. Dramatic modulation of electron transfer in protein complexes by crosslinking. Nat. Struct. Biol. 2002; 9:48-52.
37. Francisco WA, Wille G, Smith AJ, Merkler DJ, Klinman JP. Investigation of the pathway for inter-copper electron transfer in peptidyglycine alpha-amidating monooxygenase. J. Am. Chem. Soc. 2004; 126:13168-13169.
38. Wheeler KE, Nocek JM, Cull DA, Yatsunyk LA, Rosenzweig AC, Hoffman BM. Dynamic docking of cytochrome b(5) with myoglobin and alpha-hemoglobin: Heme-neutralization ’’squares” and the binding of electron-transfer-reactive configurations. J. Am. Chem. Soc. 2007; 129:3906-3917.
39. Kang SA, Crane BR. Effects of interface mutations on association modes and electron-transfer rates between proteins. Proc. Natl. Acad. Sci. U.S.A. 2005; 102:15465-15470.
40. Miyashita O, Okamura MY, Onuchic JN. Interprotein electron transfer from cytochrome c(2) to photosynthetic reaction center: Tunneling across an aqueous interface, Proc. Natl. Acad. Sci. U.S.A. 2005; 102:3558-3563.
41. Lin J, Balabin IA, Beratan DN. The nature of aqueous tunneling pathways between electron-transfer proteins. Science 2005; 310:1311-1313.
42. Cukier RI, Nocera DG. Proton-coupled electron transfer. Annu. Rev. Phys. Chem. 1998;49:337-369.
43. Hammes-Schiffer S. Theoretical perspectives on proton-coupled electron transfer reactions. Acc. Chem. Res. 2001;34:273-281.
44. Khoshtariya DE, Wei J, Liu H, Yue H, Waldeck DH. Chargetransfer mechanism for cytochrome c adsorbed on nanometer thick films. distinguishing frictional control from conformational gating. J. Am. Chem. Soc. 2003; 125:7704-7714.
45. Kang SA, Hoke KR, Crane BR. Solvent Isotope Effects on Interfacial Protein Electron Transfer in Crystals and Electrode Films. J. Am. Chem. Soc. 2006; 128:2346-2355.
46. Leys D, Scrutton NS. Electrical circuitry in biology: emerging principles from protein structure. Curr. Opin. Struct. Biol. 2004; 14:642-647.
47. Crofts AR, Guergova-Kuras M, Huang LS, Kuras R, Zhang ZL, Berry EA. Mechanism of ubiquinol oxidation by the bc(1) complex: Role of the iron sulfur protein and its mobility. Biochem. 1999; 38:15791-15806.
48. Hoffman BM, Ratner MA. Gated electron transfer: When are observed rates controlled by conformational interconversion? J. Am. Chem. Soc. 1987; 109:6237-6243.
49. Brunschwig BS, Sutin N. Directional electron transfer: Conformational interconversions and their effects on observed electron transfer rate constants. J. Am. Chem. Soc. 1989; 111:7454-7465.
50. Ruan CY, Lobastov VA, Vigliotti F, Chen S, Zewail AH. Ultrafast electron crystallography of interfacial water. Science 2004; 304:80-84.
51. Wernet P, Nordlund D, Bergmann U, Cavalleri M, Odelius M, Ogasawara H, Naslund LA, Hirsch TK, Ojamae L, Glatzel P, Pettersson LGM, Nilsson A. The Structure of the First Coordination Shell in Liquid Water. Science 2004; 304:995-999.
52. Smith JD, Cappa CD, Wilson KR, Messer BM, Cohen RC, Saykally RJ. Energetics of hydrogen bond network rearrangements in liquid water. Science 2004; 306:851-853.
53. Zubavicus Y, Grunze M. New Insights into the structure of water with ultrafast probes. Science 2004; 304:974-976.
54. Siddarth P, Marcus R. Electron-transfer reactions in proteins: A calculation of electronic coupling. J. Phys. Chem. 1990; 94:8430- 8434.
55. Balabin IA, Onuchic JN. Connection between simple models and 68. quantum chemical models for electron-transfer tunneling matrix element calculations: A Dyson’s equations-based approach. J. 69. Phys. Chem. 1996; 100:11573-11580.
56. Simonson T. Free Energy Calculations. In: Computational Biochemistry and Biophysics Becker OM, MacKerellm AD, Roux B, Watanabe M, eds. 2001. Marcel Dekker Inc., New York.
57. Leontyev IV, Basilevsky MV, Newton MD. Theory and computation of electron transfer reorganization energies with continuum and molecular solvent models. Theor. Chem. Acc. 2004; 111:110- 121.
58. Ohmine I, Tanaka H. Fluctuation, relaxations, and hydration in liquid water - hydrogen-bond rearrangement dynamics. Chem. Rev. 1993; 93:2545-2566.
59. Soper AK, Rossky PJ, eds. Special issue on water. Chem. Phys. 2000; 258.
60. Pratt LR, ed. Water thematic issue.Chem. Rev. 2002; 102.
61. Wang W, Donini O, Reyes CM, Kollman PA. Biomolecular dimulations: recent developments in force fields, simulations of enzyme catalysis, protein-ligand, protein-protein, and protein-nucleic acid noncovalent interactions. Ann. Rev. Biophys. Biomol. Struct. 2001; 30:211-243.
62. Ponder JW, Case DA. Force fields for protein simulations. Adv. Prot. Chem. 2003;66:27-85.
63. Zollner A, Pasquinelli MA, Bernhardt R, Beratan DN. Protein phosphorylation and intermolecular electron transfer: A joint experimental and computational study of a hormone biosynthesis pathway. J. Am. Chem. Soc. 2007;129:4206-4216.
64. Lindahl E, Azuara C, Koehl P, Delarue M. NOMAD-Ref: Visualization, deformation, and refinement of macromolecular structures based on all-atom normal mode analysis. Nucl. Acid Res. 2006; 34:52-56.
65. Kurisu G, Zhang H, Smith JL, Cramer WA. Structure of the cytochrome b6f complex of oxygenic photosynthesis: tuning the cavity. Science 2003; 302:1009-1014.
66. Carrell CJ, Schlarb BG, Bendall DS, Howe CJ, Cramer WA, Smith JL. Structure of the soluble domain of cytochrome f from the cyanobacterium. Phormidium laminosum, Biochemistry 1999; 38:9590-9599.
67. Sainz G, Carrell CJ, Ponamarev MV, Soriano GM, Cramer WA, Smith JL. Interruption of the internal water chain of cytochrome f impairs photosynthetic function. Biochemistry 2000; 39:9164- 9173.
68. Giese B. Electron transfer in DNA. Curr. Opin. Chem. Biol. 2002; 6:612-618.
69. Arai S, Chatake T, Ohhara T, Kurihara K, Tanaka I, Suzuki N, Fujimoto Z, Mizuno H, Niimura N. Complicated water orientations in the minor groove of the B-DNA decamer d(CCATTAATGG)2 observed by neutron diffraction measurements. Nucl. Acids Res. 2005; 33:3017-3024.
70. Tsukamoto T, Ishikawa Y, Vilkas MJ, Natsume T, Dedachi K, Kurita N. Density-functional theoretical study on hydrated DNA duplex: Effect of hydrating water molecules on HOMO distribution in DNA. Chem. Phys. Lett. 2006; 429:563-569.
Further Reading
Bendall DS. Protein electron transfer. 1996. Bios Scientific Publishers, Oxford, UK.
Chaplin M. Do we underestimate the importance of water in cell biology? Nature Reviews Mol. Cell Biol. 2006; 7:861-866.
de Vault D Parkes JH Chance B. Electron tunneling in cytochromes. Nature 1967; 215:642-644.
Eberson LE, Rees CW. Electron transfer reactions in organic chemistry. 1987. Springer-Verlag, Berlin.
Endres RG, Cox DL, Singh RRP. Colloquium: The quest for high- conductance DNA. Rev Mod.Phys. 2004; 76:195-214.
Hopfield JJ. Electron-transfer between biological molecules by thermally activated tunnelling. Proc. Natl. Acad. Sci. U.S.A. 1974; 71:3640-3644.
Jortner J, Bixon M, eds. Electron transfer - from isolated molecules to biomolecules Adv. Chem. Phys. 2003; 106-107.
Jortner J. Temperature-dependent activation-energy for electron transfer between biological molecules. J. Chem. Phys. 1976; 64:4860-4867.
Kuznetsov AM, Ulstrup J. Electron transfer in chemistry and biology: An introduction to the theory. 1999. Jon Wiley and Sons, New York.
Lippard SJ, Berg JM. Principles of bioinorganic chemistry. 1994. Mill Valley, CA, University Science Books.
May V, Kuhn O. and energy transfer dynamics in molecular systems. 2003. Wiley-VCH, Weinheim.
See Also
Chemistry of Electron Transfer Chain
Chemical Basis of Electron Transport
Electron Transfer Chemistry in Photosynthesis
Bioelectronics