Chemistry for Dummies

Part III. The Mole: The Chemist's Best Friend

In this part...

Chemists operate in the world of quantities that they can see and touch — the macroscopic world of grams, liters, and meters. They carry out chemical reactions by weighing grams of reactants, and they use grams to measure the amount of product formed. They use liters to measure the amount of gas produced. They test a solution with litmus paper to see if it’s an acid or a base.

But chemists also operate in the microscopic world of atoms and molecules. Because atoms and molecules are so very small, chemists have only just recently been able to see them, thanks to advanced technology in the most powerful of microscopes. Chemists think of acids and bases in terms of the donating and accepting of protons, not just as color changes in indicators. Models help chemists understand and predict the processes that take place in the microscopic world. These models also translate into real-life applications.

These chapters show you the bridge between the macroscopic and microscopic worlds — the mole. I explain reaction stoichiometry — how much reactant it takes to produce a particular amount of product. I introduce you to solutions and colloids, acids and bases, and gases. I show you the multitude of relationships between the properties of gases and relate them back to stoichiometry. In chemistry, everything is connected.

Chapter 10. The Mole: Can You Dig It?

In This Chapter

· Figuring out how to count by weighing

· Understanding the mole concept

· Discovering how the mole is used in chemical calculations

Chemists do a lot of things. One is to make new substances, a process called synthesis. And a logical question they ask is “How much?” “How much of this reactant do I need to make this much product?” “How much product can I make with this much reactant?” In order to answer these questions, chemists must be able to take a balanced chemical equation, expressed in terms of atoms and molecules, and convert it to grams or pounds or tons — some type of unit that they can actually weigh out in the lab. The mole concept enables chemists to move from the microscopic world of atoms and molecules to the real word of grams and kilograms and is one of the most important central concepts in chemistry. In this chapter, I introduce you to Mr. Mole.

Counting by Weighing

Suppose that you have a job packing 1,000 nuts and 1,000 bolts in big bags, and you get paid for each bag you fill. So what’s the most efficient and quickest way of counting out the nuts and bolts? Weigh out a hundred, or even ten, of each and then figure out how much a thousand of each will weigh. Fill up the bag with nuts until it weighs the amount you figured for 1,000 nuts. After you have the correct amount of nuts, use the same process to fill the bag with bolts. In other words, count by weighing; that’s one of the most efficient ways of counting large numbers of objects.

In chemistry, you count very large numbers of particles, such as atoms and molecules. To count them efficiently and quickly, you need to use the count-byweighing method, which means you need to know how much individual atoms and molecules weigh. You can get the weights of the individual atoms on the periodic table, but what about the weights of the compounds? Well, you can simply add together the weights of the individual atoms in the compound to figure the molecular weight or formula weight. (Molecular weights refer to covalently bonded compounds, and formula weights refer to both ionic and covalent compounds. Check out Chapters 6 and 7 for details on ionic and covalent bonds.)

Here’s a simple example that shows how to calculate the molecular weight of a compound: Water, H₂O, is composed of two hydrogen atoms and one oxygen atom. By looking on the periodic table, you can find that one hydrogen atom equals 1.0079 amu and one oxygen atom weighs 15.999 amu (amu stands for atomic mass units — see Chapter 3 for details). To calculate the molecular weight of water, you simply add together the atomic weights of two hydrogen atoms and one oxygen atom:

2 x 1.0079 amu = 2.016 amu (two hydrogen atoms)

1 x 15.999 amu = 15.999 amu (one oxygen atom)

2.016 amu + 15.999 amu = 18.015 amu (the weight of the water molecule)

Now try a little harder one. Calculate the formula weight of aluminum sulfate, Al₂(SO₄)₃. In this salt, you have 2 aluminum atoms, 3 sulfur atoms, and 12 oxygen atoms. After you find the individual weights of the atoms on the periodic table, you can calculate the formula weight like this:

[(2 x 26.982 amu) + (3 x 32.066 amu) + (12 x 15.999 amu)] = 332.150 amu

for the aluminum for the sulfur for the oxygen for Al₂(SO₄)₃

Pairs, Dozens, Reams, and Moles

When we humans deal with objects, we often think in terms of a convenient amount. For example, when a woman buys earrings, she normally buys a pair of them. When a man goes to the grocery store, he buys eggs by the dozen. And when I go to the office supply store, I buy copy paper by the ream.

We use words to represent numbers all the time — a pair is 2, a dozen is 12, and a ream is 500. All these words are units of measure, and they’re convenient for the objects they’re used to measure. Rarely would you want to buy a ream of earrings or a pair of paper.

Likewise, when chemists deal with atoms and molecules, they need a convenient unit that takes into consideration the very small size of atoms and molecules. There is such a unit. It’s called a mole.

Avoqadro’s number: Not in the phone book

The word mole stands for a number — 6.022 x 10²³. It’s commonly called Avogadro’s number, named after Amedeo Avogadro, the scientist who laid the groundwork for the mole principle.

Now a mole — 6.022 x 10²³ — is a really big number. When written in longhand notation, it’s

602,200,000,000,000,000,000,000

And that is why I like scientific notation.

If you had a mole of marshmallows, it would cover the United States to a depth of about 600 miles. A mole of rice grains would cover the land area of the world to a depth of 75 meters. And a mole of moles ... no, I don’t even want to think about that!

Avogadro’s number stands for a certain number of things. Normally, those things are atoms and molecules. So the mole relates to the microscopic world of atoms and molecules. But how does it relate to the macroscopic world where I work?

The answer is that a mole (abbreviated as mol) is also the number of particles in exactly 12 grams of a particular isotope of carbon (C-12). So if you have exactly 12 grams of ¹²C, you have 6.022 x 10²³ carbon atoms, which is also a mole of ¹²C atoms. For any other element, a mole is the atomic weight expressed in grams. And for a compound, a mole is the formula (or molecular) weight in grams.

Using males in the real World

The weight of a water molecule is 18.015 amu (see the section “Counting by Weighing” for how to calculate the weight of compounds). Because a mole is the formula (or molecular) weight in grams of a compound, you can now say that the weight of a mole of water is 18.015 grams. You can also say that 18.015 grams of water contains 6.022 x 10²³ H₂O molecules, or a mole of water. And the mole of water is composed of two moles of hydrogen and one mole of oxygen.

The mole is the bridge between the microscopic and the macroscopic world:

6.022 x 10²³ particles ↔ mole ↔ atomic/formula weight in grams

If you have any one of the three things — particles, moles, or grams — then you can calculate the other two.

For example, suppose you want to know how many water molecules there are in 5.50 moles of water. You can set up the problem like this:

5.50 moles x 6.022 x 10²³ molecules/mol = 3.31 x 10²⁴ molecules

Or suppose that you want to know how many moles are in 25.0 grams of water. You can set up the problem like this (and see Appendix B for more on exponential arithmetic):

You can even go from grams to particles by going through the mole. For example, how many molecules are there in 100.0 grams of carbon dioxide?

The first thing you have to do is determine the molecular weight of CO₂. Look at the periodic table to find that one carbon atom equals 12.011 amu and one oxygen atom weighs 15.999 amu. Now figure the molecular weight, like this:

[(1 x 12.011 g/mol) + (2 x 15.999 g/mol)] = 44.01 g/mol for CO₂

Now you can work the problem:

And it’s just as easy to go from particles to moles to grams.

You can also use the mole concept to calculate the empirical formula of a compound using the percentage composition data for that compound — the percentage by weight of each element in the compound. (The empirical formula indicates the different types of elements in a molecule and the lowest whole-number ratio of each kind of atom in the molecule. See Chapter 7 for details.)

When I try to determine the empirical formula of a compound, I often have percentage data available. The determination of the percentage composition is one of the first analysis that a chemist does in learning about a new compound. For example, suppose I determine that a particular compound has the following weight percentage of elements present: 26.4% Na, 36.8% S, and 36.8% O. Since I’m dealing with percentage data (amount per hundred) I will assume that I have 100 grams of the compound so that my percentages can be used as weights. I then convert each mass to moles, like this:

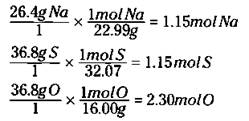
Now I can write an empirical formula of Na_1.15S_1.15O_2.30. I know that my subscripts have to be whole numbers, so I divide each of these by the smallest, 1.15, to get NaSO₂. (If a subscript is 1, it’s not shown.) I can then calculate a weight for the empirical formula, by adding together the atomic masses on the periodic table of 1 sodium (Na), 1 sulfur (S) and 2 oxygen (O). This gives me an empirical formula weight of 87.056 grams. Suppose, however, in another experiment I determined that the actual molecular weight of this compound was 174.112 grams. By dividing 174.112 grams by 87.056 grams (actual molecular weight by the empirical formula weight) I get 2. This means that the molecular formula is twice the empirical formula, so that the compound is actually Na₂S₂O₄.

Chemical Reactions and Motes

I think one of the reasons I enjoy being a chemist is that I like to cook. I see a lot of similarities between cooking and chemistry. A chemist takes certain things called reactants and makes something new from them. A cook does the same thing. He or she takes certain things called ingredients and makes something new from them.

For example, I like to fix Fantastic Apple Tarts (FATs). My recipe looks something like this:

apples + sugar + flour + spices = FATs

No, wait. My recipe has amounts in it. It looks more like this:

4 cups of apples + 3 cups of sugar + 2 cups of flour + 1/10 cup of spices = 12 FATs

My recipe tells me how much of each ingredient I need and how many FATs I can make. I can even use my recipe to calculate how much of each ingredient I need for a particular number of FATs. For example, suppose that I’m giving a big dinner party, and I need 250 FATs. I can use my recipe to calculate the amount of apples, sugar, flour, and spices I need. Here, for example, is how I calculate how much sugar I need:

And I can do the same for the apples, flour, and spices by simply changing the ratio of each ingredient (as a multiple of 12 FATs).

The balanced chemical equation allows you to do the same thing. For example, look at my favorite reaction, the Haber process, which is a method for preparing ammonia (NH₃) by reacting nitrogen gas with hydrogen gas:

In Chapter 8, I use this reaction over and over again for various examples (like I said, it’s my favorite reaction) and explain that you can read the reaction like this: 1 molecule of nitrogen gas reacts with 3 molecules of hydrogen gas to yield 2 molecules of ammonia.

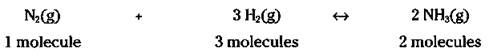
Now, you can scale everything up by a factor of 12:

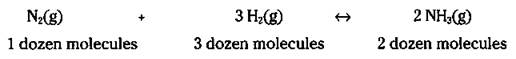
You can even scale it up by 1,000:

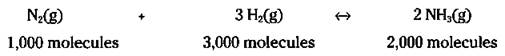
Or how about a factor of 6.023 x 10²³:

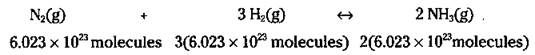
Wait a minute! Isn’t 6.023 x 10²³ a mole? So you can write the equation like this:

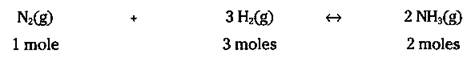
That’s right — not only can those coefficients in the balanced chemical equation represent atoms and molecules, but they can also represent the number of moles.

Now take another look at my recipe for FATs:

4 cups of apples + 3 cups of sugar + 2 cups of flour + 1/10 cup of spices = 12 FATs

I have a problem. When I go to the grocery store, I don’t buy fresh apples by the cup. Nor do I buy sugar or flour by the cup. I buy all these things by the pound. Now I buy a large excess, but because I’m frugal (translate as cheap), I want to figure as closely as I can the amount I really need. If I can determine the weight per cup for each ingredient, I’ll be okay. So I weigh the ingredients and get

1 cup of apples = 0.5 lbs; 1 cup of sugar = 0.7 lbs; 1 cup of flour = 0.3 lbs; and 1 cup of spices = 0.2 lbs

Now I can substitute the measurements into my recipe:

Now if I want to know how many pounds of apples I need to make 250 FATs, I can set up the equation this way:

I can figure out how much of each ingredient I need (based on weight), just by using the correct ingredient weight per cup.

The exact same thing is true with chemical equations. If you know the formula weight of the reactants and product, you can calculate how much you need and how much you’ll get. For example, check out that Haber reaction again:

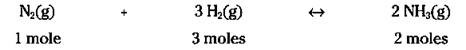
All you need to do is figure the molecular weights of each reactant and product, and then incorporate the weights into the equation. Use the periodic table to find the weights of the atoms and the compound (see the section “Counting by Weighing,” earlier in this chapter, for the directions) and multiply those numbers by the number of moles, like this:

1(28.014 g/mol) 3(2.016 g/mol) 2(17.031 g/mol)

How much needed, how much made: Reaction stoichiometry

Once you have the weight relationships in place, you can do some stoichiometry problems. Stoichiometry refers to the mass relationship in chemical equations.

Look at my favorite reaction — you guessed it — the Haber process:

Suppose that you want to know how many grams of ammonia can be produced from the reaction of 75.00 grams of nitrogen with excess hydrogen. The mole concept is the key. The coefficients in the balanced equation are not only the number of individual atoms or molecules but also the number of moles.

First, you can convert the 75.00 grams of nitrogen to moles of nitrogen. Then you use the ratio of the moles of ammonia to the moles of nitrogen from the balanced equation to convert to moles of ammonia. Finally you take the moles of ammonia and convert it to grams. The equation looks like this:

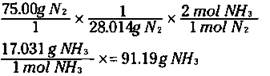
The ratio of the mol NH₃/mol N₂ is called a stoichiometric ratio. This ratio enables you to convert from the moles of one substance in a balanced chemical equation to the moles of another substance.

Getting tired of the Haber process? (Me? Never.) Take a look at another reaction — the reduction of rust (Fe₂O₃) to iron metal by treatment with carbon (coke). The balanced chemical reaction looks like this:

When you get ready to work stoichiometry types of problems, you must start with a balanced chemical equation. If you don’t have it to start with, you’ve got to go ahead and balance the equation.

In this example, the formula weights you need are

ü Fe₂O₃: 159.69 g/mol

ü C: 12.01 g/mol

ü Fe: 55.85 g/mol

ü CO₂: 44.01 g/mol

Suppose that you want to know how many grams of carbon it takes to react with 1.000 kilogram of rust. You need to convert the kilogram of rust to grams and convert the grams to moles of rust. Then you can use a stoichiometric ratio to convert from moles of rust to moles of carbon and finally to grams. The equation looks like this:

You can even calculate the number of carbon atoms it takes to react with that 1.000 kilogram of rust. Basically, you use the same conversions, but instead of converting from moles of carbon to grams, you convert from moles of carbon to carbon atoms using Avogadro’s number:

2.839 x 10²⁴ C atoms

Now I want to show you how to calculate the number of grams of iron produced from reacting 1.000 kilogram of rust with excess carbon. It’s the same basic process as before — kilograms of rust to grams of rust to moles of rust to moles of iron to grams of iron:

So you predict that you’ll get 699.5 grams of iron metal formed. What if, however, you carry out this reaction and only get 525.0 grams of iron metal formed? There may be several reasons that you produce less than you expect, such as sloppy technique or impure reactants. It may also be quite likely that the reaction is an equilibrium reaction, and you’ll never get 100 percent conversion from reactants to products. (Turn to Chapter 8 for details on equilibrium reactions.) Wouldn’t it be nice if there was a way to label the efficiency of a particular reaction? There is. It’s called the percent yield.

Where did it go? Percent yield

In almost any reaction, you’re going to produce less than expected. You may produce less because most reactions are equilibrium reactions (see Chapter 8) or because some other condition comes into play. Chemists can get an idea of the efficiency of a reaction by calculating the percent yield for the reaction using this equation:

The actual yield is how much of the product you get when you carry out the reaction. The theoretical yield is how much of the product you calculate you’ll get. The ratio of these two yields gives you an idea about how efficient the reaction is. For the reaction of rust to iron (see the preceding section), your theoretical yield is 699.5 grams of iron; your actual yield is 525.0 grams. Therefore, the percent yield is

A percent yield of about 75 percent isn’t too bad, but chemists and chemical engineers would rather see 90+ percent. One plant using the Haber reaction has a percent yield of better than 99 percent. Now that’s efficiency!

Running out of something and leaving something behind: Limiting reactants

I love to cook, and I’m always hungry. So I want to talk about making some ham sandwiches. Because I’m a chemist, I can write an equation for a ham sandwich lunch:

2 pieces of bread + 1 ham + 1 cheese →1 ham sandwich

Suppose I check my supplies and find that I have 12 pieces of bread, 5 pieces of ham, and 10 slices of cheese. How many sandwiches can I make? I can make five, of course. I have enough bread for six sandwiches, enough ham for five, and enough cheese for ten. But I’m going to run out of ham first — I’ll have bread and cheese left over. And the ingredient I run out of first really limits the amount of product (sandwiches) I’ll be able to make; it can be called the limiting ingredient

The same is true of chemical reactions. Normally, you run out of one of the reactants and have some others left over. (In some of the problems sprinkled throughout this chapter, I tell you which reactant is the limiting one by saying you have an excess of the other reactant(s).)

In this section, I show you how you can calculate which reactant is the limiting reactant.

Here is a reaction between ammonia and oxygen:

Suppose that you start out with 100.0 grams of both ammonia and oxygen, and you want to know how many grams of NO (nitrogen monoxide, sometimes called nitric oxide) you can produce. You must determine the limiting reactant and then base your stoichiometric calculations on it.

In order to figure out which reactant is the limiting reactant, you can calculate the mole-to-coefficient ratio: You calculate the number of moles of both ammonia and oxygen, and then you divide each by their coefficient in the balanced chemical equation. The one with the smallest mole-to-coefficient ratio is the limiting reactant. For the reaction of ammonia to nitric oxide, you can calculate the mole-to-coefficient ratio for the ammonia and oxygen like this:

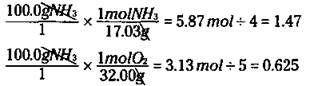
Ammonia has a mole-to-coefficient ratio of 1.47, and oxygen has a ratio of 0.625. Because oxygen has the lowest ratio, oxygen is the limiting reactant, and you need to base your calculations on it.

That 75.02 grams NO is your theoretical yield. But you can even calculate the amount of ammonia left over. You can figure the amount of ammonia consumed with this equation:

You started with 100.0 grams of ammonia, and you used 42.58 grams of it. The difference (100 grams - 42.58 grams = 57.42 grams) is the amount of ammonia left over.