Chemistry for Dummies

Part III. The Mole: The Chemist's Best Friend

Chapter 13. Balloons, Tires, and Scuba Tanks: The Wonderful World of Gases

In This Chapter

· Accepting the Kinetic Molecular Theory of Gases

· Figuring out pressure

· Coming to understand the gas laws

Gases are all around you. Because gases are generally invisible, you may not think of them directly, but you’re certainly aware of their properties. You breathe a mixture of gases that you call air. You check the pressure of your automobile tires, and you check the atmospheric pressure to see if a storm is coming. You burn gases in your gas grill and lighters. You fill birthday balloons for your loved ones.

The properties of gases and their interrelationships are important to you. Is there enough pressure in my tires? How big is that balloon going to be? Is there enough air in my scuba tanks? The list goes on and on.

In this chapter, I introduce you to gases at both the microscopic and macroscopic levels. I show you one of science’s most successful theories — the Kinetic Molecular Theory of Gases. And I explain the macroscopic properties of gases and show you the important interrelationships among them. I also show you how these relationships come into play in reaction stoichiometry. This chapter is a real gas!

Microscopic View of Gases: The Kinetic Molecular Theory

A theory is useful to scientists if it describes the physical system they’re examining and allows them to predict what will happen if they change some variable. The Kinetic Molecular Theory of Gases does just that. It has limitations — all theories do — but it’s one of the most useful theories in chemistry. This section describes the theory’s basic postulates — assumptions, hypotheses, axioms (pick your favorite word) you can accept as being true.

ü Postulate 1: Gases are composed of tiny particles, either atoms or molecules.

Unless you’re discussing matter at greatly elevated temperatures, the particles referred to as gases tend to be relatively small. The more massive particles clump together to form liquids or even solids. So gases are normally small with relatively low atomic and molecular weights.

ü Postulate 2: The gas particles are so small when compared to the distances between them that the volume the gas particles themselves take up is negligible and is assumed to be zero.

These gas particles do take up some volume — that’s one of the properties of matter. But if the gas particles are small (which they are), and there aren’t many of them in a container, you say that their volume is negligible when compared to the volume of the container or the space between the gas particles. This explains why gases are compressible. There’s a lot of space between the gas particles, so they can be squeezed together. This isn’t true in solids and liquids, where the particles are much closer together. (Chapter 2 covers the various states of matter, if you want to have a look-see at the differences between solids, liquids, and gases.)

The concept of a quantity being negligible is used a lot in chemistry. An example is in Chapter 12 where I use the acid ionization constant (Kg) of a weak acid, ignoring the amount of weak acid that has ionized compared to the initial concentration of the acid.

In the real world, I like to compare this negligible concept to finding a dollar in the street. If you have no money at all, then that dollar represents a sizable quantity of cash (perhaps your next meal). But if you’re a multimillionaire, then that dollar doesn’t represent much at all. It may as well be a piece of scrap paper. You may not even pick it up. (I really can’t imagine being that rich.) Its value is negligible when compared to the rest of your wealth. This is what I’m saying with respect to the volume of the gas particles — sure, they have a volume, but it’s so small that it’s insignificant when compared with the distance between the gas particles and the volume of the container.

ü Postulate 3: The gas particles are in constant random motion, moving in straight lines and colliding with the inside walls of the container.

The gas particles are always moving in a straight-line motion. (Gases have a higher kinetic energy — energy of motion — associated with them when compared to solids or liquids; see Chapter 2.) They continue to move in these straight lines until they collide with something — either with each other or with the inside walls of the container. The particles also all move in different directions, so the collisions with the inside walls of the container tend to be uniform over the entire inside surface. You can observe this uniformity by simply blowing up a balloon. The balloon is spherical because the gas particles are hitting all points of the inside walls the same. The collision of the gas particles with the inside walls of the container is called pressure. The idea that the gas particles are in constant, random, straight-line motion explains why gases uniformly mix if put in the same container. It also explains why, when you drop a bottle of cheap perfume at one end of the room, the people at the other end of the room are able to smell it right away.

ü Postulate 4: The gas particles are assumed to have negligible attractive or repulsive forces between each other.

In other words, the gas particles are assumed to be totally independent, neither attracting nor repelling each other. That said, it’s hair-splitting time. This statement is actually false; if it were true, chemists would never be able to liquefy a gas, which they can. But the reason you can accept this assumption as true is that the attractive and repulsive forces are generally so small that they can safely be ignored. The assumption is most valid for nonpolar gases, such as hydrogen and nitrogen, because the attractive forces involved are London forces. However, if the gas molecules are polar, as in water and HCl, this assumption can become a problem. (Turn to Chapter 7 for the scoop about London forces and polar things — all related to the attraction between molecules.)

ü Postulate 5: The gas particles may collide with each other. These collisions are assumed to be elastic, with the total amount of kinetic energy of the two gas particles remaining the same.

Not only do the gas particles collide with the inside walls of the container, they also collide with each other. If they hit each other, no kinetic energy is lost, but kinetic energy may be transferred from one gas particle to the other. For example, imagine two gas particles — one moving fast and the other moving slow — colliding. Kinetic energy is transferred from the faster particle to the slower particle. The one that’s moving slow bounces off the faster particle and moves away at a greater speed than before, while the one that’s moving fast bounces off the slower particle and moves away at a slower speed. The total amount of kinetic energy remains the same, but one gas particle loses energy and the other gains energy. This is the principle behind pool — you transfer kinetic energy from your moving pool stick to the cue ball to the ball you’re aiming at.

ü Postulate 6: The Kelvin temperature is directly proportional to the average kinetic energy of the gas particles.

The gas particles aren’t all moving with the same amount of kinetic energy. A few are moving relatively slow and a few are moving very fast, but most are somewhere in between these two extremes. Temperature, particularly as measured using the Kelvin temperature scale, is directly related to the average kinetic energy of the gas. If you heat the gas so that the Kelvin temperature (K) increases, the average kinetic energy of the gas also increases. (To calculate the Kelvin temperature, add 273 to the Celsius temperature: K = °C + 273. Temperature scales and average kinetic energy are all tucked neatly into Chapter 2.)

REMEMBER. A gas that obeys all the postulates of the Kinetic Molecular Theory is called an ideal gas. Obviously, no real gas obeys the assumptions made in the second and fourth postulates exactly. But a nonpolar gas at high temperatures and low pressure (concentration) approaches ideal gas behavior.

I’m Under Pressure — Atmospheric Pressure, That Is

Although you’re not in a container, the gas molecules of the atmosphere are constantly hitting you, your books, your computer, and everything, and exerting a force called atmospheric pressure. Atmospheric pressure is measured using an instrument called a barometer.

Measuring atmospheric pressure: The barometer

If you get a complete weather report, the atmospheric pressure is normally included. You can get an idea about changes in the weather by observing whether the atmospheric pressure is rising or falling. The atmospheric pressure is measured using a barometer, and Figure 13-1 shows the components of one.

A barometer is composed of a long glass tube that’s closed at one end and totally filled with a liquid. You can use water, but the tube would have to be very long (about 35 feet long), making for a rather inconvenient barometer.

So it makes more sense to use mercury because it’s a very dense liquid. The tube filled with mercury is inverted into an open container of mercury so that the open end of the tube is under the surface of the mercury in the container. A couple of things now take place. The force of gravity pulls the mercury in the tube down, causing it to drain out into the container. The weight of the gases in the atmosphere exert a force downward on the mercury in the open container and force it up into the tube. Sooner or later, these forces balance, and the mercury in the tube comes to rest at a certain height from the top of the pool of mercury in the container. The greater the pressure of the atmosphere, the higher the mercury column that can be measured in the tube; the lower the pressure of the atmosphere (for example, at the top of a tall mountain), the shorter the column. At sea level, the column is 760 millimeters high, the so-called normal atmospheric pressure.

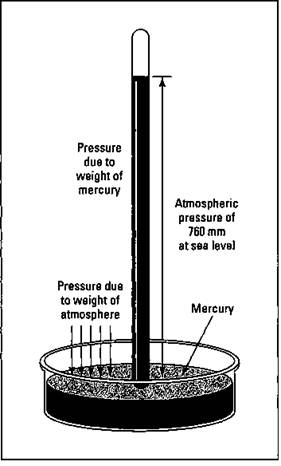
Figure 13-1: A barometer.

Atmospheric pressure can be expressed a number of different ways. It can be expressed in millimeters of mercury (mm Hg); atmospheres (atm), a unit of pressure where 1 atmosphere is the pressure at sea level; torr, a unit of pressure where 1 torr equals 1 millimeter of mercury; pounds per square inch (psi); pascals (Pa), a unit of pressure where 1 pascal equals 1 newton per square meter (don’t worry about what a newton is; just trust me that this stuff is a way to express pressure); or kilopascals (kPa), where 1 kilopascal equals 1,000 pascals.

So you can express the atmospheric pressure at sea level as

760 mm Hg = 1 atm = 760 torr = 14.69 psi = 101,325 Pa = 101.325 kPa

Note that sometimes you also hear atmospheric pressure reported as inches of mercury (1 atm = 29.921 in Hg). In this book, I primarily use atmospheres and torr, with an occasional millimeter of Hg. Variety is the spice of life.

Measuring confined gas pressure: The manometer

You can measure the pressure of a gas confined in a container by using an apparatus called a manometer. (It’s pronounced man-AH-muh-ter, not mano-meter:) Figure 13-2 shows the components of a manometer.

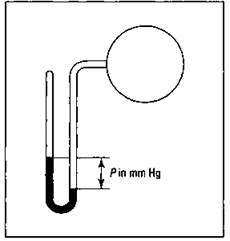
Figure 13-2: The manometer.

A manometer is kind of like a barometer. The container of gas is attached to a U-shaped piece of glass tubing that’s partially filled with mercury and sealed at the other end. Gravity pulls down the mercury column at the closed end. The mercury is then balanced by the pressure of the gas in the container. The difference in the two mercury levels represents the amount of gas pressure.

Gases Obey Laws, Too — Gas Laws

Various scientific laws describe the relationships between four of the important physical properties of gases:

ü Volume

ü Pressure

ü Temperature

ü Amount

This section covers those various laws. Boyle’s, Charles’s, and Gay-Lussac’s Laws each describe the relationship between two properties while keeping the other two properties constant. (In other words, you take two properties, change one, and then see its effect on the second — while keeping the remaining properties constant.) Another law — a combo of Boyle’s, Charles’s, and Gay-Lussac’s individual laws — enables you to vary more than one property at a time.

But that combo law doesn’t let you vary the physical property of amount. Avogadro’s Law, however, does. And there’s even an ideal gas law, which lets you take into account variations in all four physical properties.

Yes, this section is so chock-full of laws, it’ll probably give you gas just trying to digest it.

Boyle's Law: Nothing to do with boiling

Boyle’s Law, named after Robert Boyle, a seventeenth-century English scientist, describes the pressure-volume relationship of gases if the temperature and amount are kept constant. Figure 13-3 illustrates the pressure-volume relationship using the Kinetic Molecular Theory.

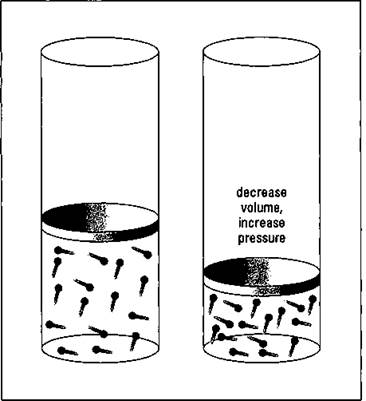
Figure 13-3: Pressure- volume relationship of gases — Boyle's Law.

The left-hand cylinder in the figure contains a certain volume of gas at a certain pressure. (Pressure is the collision of the gas particles with the inside walls of the container.) When the volume is decreased, the same number of gas particles are now contained in a much smaller volume and the number of collisions increases significantly. Therefore, the pressure is greater.

Boyle’s Law states that there’s an inverse relationship between the volume and pressure. As the volume decreases, the pressure increases, and vice versa.

Boyle determined that the product of the pressure and the volume is a constant (k):

Now consider a case where you have a gas at a certain pressure (P₁) and volume (V₁). If you change the volume to some new value (V₂), the pressure also changes to a new value (P₂). You can use Boyle’s Law to describe both sets of conditions:

The constant, k, is going to be the same in both cases. So you can say

P₁V₁ = P₂V₂ (with temperature and amount constant)

This equation is another statement of Boyle’s Law — and it’s really a more useful one, because you’ll normally deal with changes in pressure and volume. If you know three of the preceding quantities, you can calculate the fourth one. For example, suppose that you have 5.00 liters of a gas at 1.00 atm pressure, and then you decrease the volume to 2.00 liters. What’s the new pressure?

To find the answer, use the following setup:

Substituting 1.00 atm for P₁, 5.00 liters for V₁, and 2.00 liters for V₂, you get

(1.00 atm)(5.00 liters) = P₂(2.00 liters)

Now solve for P₂:

(1.00 atm)(5.00 liters)/2.00 liters = P₂ = 2.50 atm

The answer makes sense, because you decreased the volume and the pressure increased, which is exactly what Boyle’s law says.

Charles's Law: Don't call me Chuck

Charles’s Law, named after Jacques Charles, a nineteenth-century French chemist, has to do with the relationship between volume and temperature, keeping the pressure and amount constant. You run across situations dealing with this relationship in everyday life, especially in terms of the heating and cooling of balloons.

Figure 13-4 shows the temperature-volume relationship.

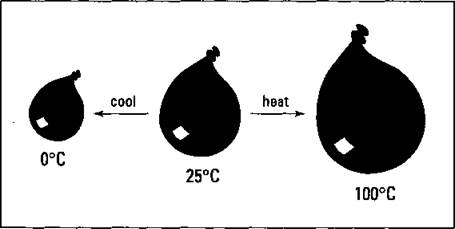
Figure 13-4: The temperature-volume relationship of gases — Charles's Law.

Look at the balloon in the middle of Figure 13-4. What do you think would happen to the balloon if you placed it in the freezer? It’d get smaller. Inside the freezer, the external pressure, or atmospheric pressure, is the same, but the gas particles inside the balloon aren’t moving as fast, so the volume shrinks to keep the pressure constant. If you heat the balloon, the balloon expands and the volume increases. This is a direct relationship — as the temperature increases, the volume increases, and vice versa.

Jacques Charles developed the mathematical relationship between temperature and volume. He also discovered that you must use the Kelvin (K) temperature when working with gas law expressions.

REMEMBER. In gas law calculations, the Kelvin temperature must be used.

Charles’s Law says that the volume is directly proportional to the Kelvin temperature. Mathematically, the law looks like this:

V = bT or V/T = b (where b is a constant)

If the temperature of a gas with a certain volume (V₁) and Kelvin temperature (T₁) is changed to a new Kelvin temperature (T₂), the volume also changes (V₂).

The constant, b, is the same, so

V₁/T₁ = V₂/T₂ (with the pressure and amount of gas held constant and temperature expressed in K)

If you have three of the quantities, you can calculate the fourth. For example, suppose you live in Alaska and are outside in the middle of winter, where the temperature is -23 degrees Celsius. You blow up a balloon so that it has a volume of 1.00 liter. You then take it inside your home, where the temperature is a toasty 27 degrees Celsius. What’s the new volume of the balloon?

First, convert your temperatures to Kelvin by adding 273 to the Celsius temperature:

-23 °C + 273 = 250 K (outside)

27 °C + 273 = 300 K (inside)

Now you can solve for V₂, using the following setup:

Multiply both sides by T₂ so that V₂ is on one side of the equation by itself:

Then substitute the values to calculate the following answer:

[(1.00 liter)(300 K)]/250 K = V₂ = 1.20 liters

It’s a reasonable answer, because Charles’s Law says that if you increase the Kelvin temperature, the volume increases.

Gay-Lussac's Law

Gay-Lussac’s Law, named after the 19th century French scientist Joseph-Louis Gay-Lussac deals with the relationship between the pressure and temperature of a gas if its volume and amount are held constant. Imagine, for example, that you have a metal tank of gas. The tank has a certain volume, and the gas inside has a certain pressure. If you heat the tank, you increase the kinetic energy of the gas particles. So they’re now moving much faster, and they’re not only hitting the inside walls of the tank more often but also with more force. The pressure has increased.

Gay-Lussac’s Law says that the pressure is directly proportional to the Kelvin temperature. Figure 13-5 shows this relationship.

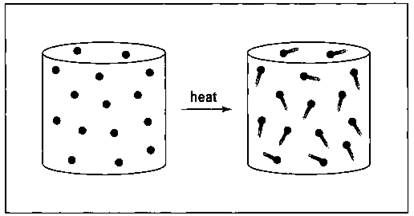
Figure 13-5: The pressure-temperature relationship of gases — Gay-Lussac's Law.

Mathematically, Gay-Lussac’s Law looks like this:

P = kT (or P/T = k at constant volume and amount)

Consider a gas at a certain Kelvin temperature and pressure (T₁ and P₁, with the conditions being changed to a new temperature and pressure (T₂ and P₂):

If you have a tank of gas at 800 torr pressure and a temperature of 250 Kelvin, and it’s heated to 400 Kelvin, what’s the new pressure?

Starting with , multiply both sides by T₂ so you can solve for P₂:

Now substitute the values to calculate the following answer:

[(800 torr)(400 K)]/250 K = P₂ = 1,280 torr

This is a reasonable answer because if you heat the tank, the pressure should increase.

The combined gas law

All the preceding examples assume that two properties are held constant and one property is changed to see its effect on a fourth property. But life is rarely that simple. How do you handle situations in which two or even three properties change? You can treat each one separately, but it sure would be nice if you had a way to combine things so that wouldn’t be necessary.

Actually, there is a way. You can combine Boyle’s Law, Charles’s Law, and Gay-Lussac’s Law into one equation. Trust me, you don’t want me to show you exactly how it’s done, but the end result is called the combined gas law, and it looks like this:

Just like in the preceding examples, P is the pressure of the gas (in atm, mm Hg, torr, and so on), V is the volume of the gas (in appropriate units), and T is the temperature (in Kelvin). The 1 and 2 stand for the initial and final conditions, respectively. The amount is still held constant: No gas is added, and no gas escapes. There are six quantities involved in this combined gas law; knowing five allows you to calculate the sixth.

For example, suppose that a weather balloon with a volume of 25.0 liters at 1.00 atm pressure and a temperature of 27 degrees Celsius is allowed to rise to an altitude where the pressure is 0.500 atm and the temperature is -33 degrees Celsius. What’s the new volume of the balloon?

Before I show you how to work this problem, do a little reasoning. The temperature is decreasing, so that should cause the volume to decrease (Charles’s Law). However, the pressure is also decreasing, which should cause the balloon to expand (Boyle’s Law). These two factors are competing, so at this point, you don’t know which will win out.

You’re looking for the new volume (V₂), so rearrange the combined gas law to obtain the following equation (by multiplying each side by T₂ and dividing each side by P₂, which puts V₂ by itself on one side):

Now identify your quantities:

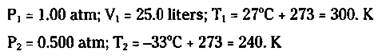
Now substitute the values to calculate the following answer:

[(1.00 atm)(25.0 liters)(240. K)]/[(0.500 atm)(300. K)] = V₂= 40.0 liters

Because the volume increased overall in this case, Boyle’s Law had a greater effect than Charles’s Law.

Avogadro's Law

The combined gas equation gives you a way to calculate changes involving pressure, volume, and temperature. But you still have the problem of amount to deal with. In order to account for amount, you need to know another law. Amedeo Avogadro (the same Avogadro that gave us his famous number of particles per mole — see Chapter 10) determined, from his study of gases, that equal volumes of gases at the same temperature and pressure contain equal numbers of gas particles. So Avogadro’s Law says that the volume of a gas is directly proportional to the number of moles of gas (number of gas particles) at a constant temperature and pressure. Mathematically, Avogadro’s Law looks like this:

V = kn (at constant temperature and pressure)

In this equation, k is a constant and n is the number of moles of gas. If you have a number of moles of gas (n₁) at one volume (V₁), and the moles change due to a reaction (n₂), the volume also changes (V₂), giving you the equation

I’m not going to work any problems with this law, because it’s basically the same idea as the other gets laws covered in this chapter.

REMEMBER. A very useful consequence of Avogadro’s Law is that the volume of a mole of gas can be calculated at any temperature and pressure. An extremely useful form to know when calculating the volume of a mole of gas is 1 mole of any gas at STP occupies 22.4 liters. STP in this case is not an oil or gas additive. It stands for Standard Temperature and Pressure.

ü Standard Pressure: 1.00 atm (760 torr or mm Hg)

ü Standard Temperature: 273 K

This relationship between moles of gas and liters gives you a way to convert the gas from a mass to a volume. For example, suppose that you have 50.0 grams of oxygen gas (O₂), and you want to know its volume at STP. You can set up the problem like this (see Chapters 10 and 11 for the nuts and bolts of using moles in chemical equations):

You now know that the 50.0 grams of oxygen gas occupies a volume of 35.0 liters at STP. But what if the gas is not at STP? What’s the volume of 50.0 grams of oxygen at 2.00 atm and 27.0 degrees Celsius? In the next section, I show you a really easy way of doing this problem. But right now, you can use the combined gas law, because you know the volume at STP:

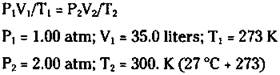
Solving for V₂, you calculate the following answer:

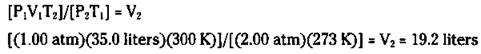
The ideal gas equation

If you take Boyle’s Law, Charles’s Law, Gay-Lussac’s Law, and Avogadro’s Law and throw them into a blender, turn the blender on high for a minute, and then pull them out, you get the ideal gas equation — a way of working in volume, temperature, pressure, and amount. The ideal gas equation has the following form:

The Prepresents pressure in atmospheres (atm), the Vrepresents volume in liters (L), the n represents moles of gas, the T represents the temperature in Kelvin (K), and the R represents the ideal gas constant, which is 0.0821 liters atm/K mol.

Using the value of the ideal gas constant, the pressure must be expressed in atm, and the volume must be expressed in liters. You can calculate other ideal gas constants if you really want to use torr and milliliters, for example, but why bother? It’s easier to memorize one value for R and then remember to express the pressure and volume in the appropriate units. Naturally, you’ll always express the temperature in Kelvin when working any kind of gas law problem.

That said, now I want to show you an easy way to convert a gas from a mass to a volume if the gas is not at STP. What’s the volume of 50.0 grams of oxygen at 2.00 atm and 27.0 degrees Celsius?

The first thing you have to do is convert the 50.0 grams of oxygen to moles using the molecular weight of O₂:

(50.0 grams)(1 mol/32.0 grams) = 1.562 mol

Now take the ideal gas equation and rearrange it so you can solve for V:

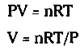
Add your known quantities to calculate the following answer:

V = [(1.562 mol)(0.0821 liters atm/Kmol)(300 K)]/2.00 atm = 19.2 liters

This is the exact same answer you get in the preceding section, but it’s calculated in a much more straightforward way.

Stoichiometry and the Gas Laws

The ideal gas equation (and even the combined gas equation) allows chemists to work stoichiometry problems involving gases. (Chapter 10 is your key to the world of stoichiometry.) In this section, you’re going to use the ideal gas equation to do such a problem, using a classic chemistry experiment — the decomposition of potassium chlorate to potassium chloride and oxygen by heating:

Here’s your mission: Figure out the volume of oxygen gas produced at 700 torr and 27 degrees Celsius from the decomposition of 25.0 grams of KClO₃.

First, you need to calculate the number of moles of oxygen gas produced:

Next, convert the temperature to Kelvin and the pressure to atm:

27 °C + 273 = 300 K

700 torr/760 torr/atm = 0.9211 atm

Now put everything in the ideal gas equation:

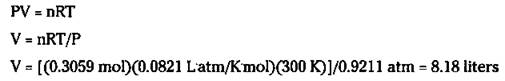
Mission accomplished.

Dalton's and Graham's Laws

This section covers a couple of miscellaneous but fine gas laws you should have a nodding acquaintance with. One relates to partial pressures and the other to gaseous effusion/diffusion. Party on.

Dalton's Law

Dalton’s Law of partial pressures says that in a mixture of gases, the total pressure is the sum of the partial pressures of each individual gas.

If you have a mixture of gases — gas A, gas B, gas C, and so on — then the total pressure of the system is simply the sum of the pressures of the individual gases. Mathematically, the relationship can be expressed like this:

When working stoichiometry problems like the one in the preceding section involving the decomposition of potassium chlorate, the oxygen is normally collected over water by displacement and the volume is then measured. However, in order to get the pressure of just the oxygen, you have to subtract the pressure due to the water vapor. You have to mathematically “dry out” the gas.

Suppose, for example, that a sample of oxygen is collected over water at a total pressure of 755 torr at 20 degrees Celsius. And suppose that your job, you lucky dawg, is to calculate the pressure of the oxygen.

You know that the total pressure is 755 torr. Your first task is to reference a table of vapor pressures of water versus temperature. (You can find such a table in a variety of places, such as the Chemical Rubber Company (CRC) Handbook.) After looking at the table, you determine that the partial pressure of water at 20 degrees Celsius is 17.5 torr. Now you’re ready to calculate the pressure of the oxygen:

Knowing the partial pressure of gases like oxygen is important in deep sea diving and the operation of respirators in hospitals.

Graham's Law

Place a few drops of a strong perfume on a table at one end of a room, and soon people at the other end of the room can smell it. This process is called gaseous diffusion, the mixing of gases due to their molecular motion.

Place a few drops of that same perfume inside an ordinary rubber balloon and blow it up. Very soon you’ll be able to smell the perfume outside of the balloon as it makes its way through the microscopic pores of the rubber. This process is called gaseous effusion, the movement of a gas through a tiny opening. The same process of effusion is responsible for the helium being quickly lost from rubber balloons.

Thomas Graham determined that the rates of diffusion and effusion of gases are inversely proportional to the square roots of their molecular or atomic weights. This is Graham’s Law. In general, it says that the lighter the gas, the faster it will effuse (or diffuse). Mathematically, Graham’s Law looks like this:

Suppose that you fill two rubber balloons to the same size, one with hydrogen (H₂) and the other with oxygen (O₂). The hydrogen, being lighter, should effuse through the balloon pores faster. But how much faster? Using Graham’s Law, you can determine the answer:

The hydrogen should effuse out four times as fast as the oxygen.