Chemistry for Dummies

Appendix C. Unit Conversion Method

You’ll find that it’s often unclear how to actually set up chemistry problems to solve them. A scientific calculator will handle the math, but it won’t tell you what you need to multiply or what you need to divide.

That’s why you need to know about the unit conversion method, which is sometimes called the factor label method. It will help you set up chemistry problems and calculate them correctly. Two basic rules are associated with the unit conversion method:

ü Rule 1: Always write the unit and the number associated with the unit. Rarely in chemistry will you have a number without a unit. Pi is the major exception that comes to mind.

ü Rule 2: Carry out mathematical operations with the units, canceling them until you end up with the unit you want in the final answer. In every step, you must have a correct mathematical statement.

How about an example so you can see those rules in action? Suppose that you have an object traveling at 75 miles per hour, and you want to calculate its speed in kilometers per second. The first thing you do is write down what you start with:

Note that per Rule #1, the equation shows the unit and the number associated with it.

Now convert miles to feet, canceling the unit of miles per Rule #2:

Next, convert feet to inches:

Convert inches to centimeters:

Convert centimeters to meters:

And convert meters to kilometers:

Stop and stretch. Now you can start working on the denominator of the original fraction by converting hours to minutes:

Next, convert minutes to seconds:

Now that you have the units of kilometers per second (km/s), you can do the math to get the answer:

0.033528 km/s

Note that you can round off your answer to the correct number of significant figures. Appendix D gives you details on how to do so, if you’re interested. The rounded-off answer to this problem is

0.034 km/s or 3.4 x 10^-2 km/s

Note that although the setup of the preceding example is correct, it’s certainly not the only correct setup. Depending on what conversion factors you know and use, there may be many correct ways to set up a problem and get the correct answer.

Now I want to show you one more example to illustrate an additional point. Suppose that you have an object with an area of 35 inches squared, and you want to figure out the area in meters squared. Again, the first step is to write down what you start with:

Now convert from inches to centimeters, but remember that you have to cancel inches squared. You must square the inches in the new fraction, and if you square the unit, you have to square the number also. And if you square the denominator, you have to square the numerator, too:

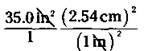
Now convert from centimeters squared to meters squared in the same way:

Now that you have the units of meters squared (m²), you can do the math to get your answer:

0.0225806 m²

And if you want to round off your answer to the correct number of significant figures (see Appendix D for details), you get

0.023 m² or 2.3 x 10^-2 m²

With a little practice, you’ll really like and appreciate the unit conversion method. It got me through my introductory physics course!