Chemistry for Dummies

Part I. Basic Concepts of Chemistry

Chapter 3. Something Smaller Than an Atom? Atomic Structure

In This Chapter

· Taking a look at the particles that make up an atom

· Finding out about isotopes and ions

· Coming to understand electron configurations

· Discovering the importance of valence electrons

I remember learning about atoms as a child in school. My teachers called them building blocks and, in fact, we used blocks and Legos to represent atoms. I also remember being told that atoms were so small that nobody would ever see one. Imagine my surprise years later when the first pictures of atoms appeared. They weren’t very detailed, but they did make me stop and think how far science had come. I am still amazed when I see pictures of atoms.

In this chapter, I tell you about atoms, the fundamental building blocks of the universe. I cover the three basic particles of an atom — protons, neutrons, and electrons — and show you where they’re located. And I use a slew of pages on electrons themselves, because chemical reactions (where a lot of chemistry comes into play) depend on the loss, gain, or sharing of them.

Subatomic Particles: So That's What's in an Atom

The atom is the smallest part of matter that represents a particular element. For quite a while, the atom was thought to be the smallest part of matter that could exist. But in the latter part of the nineteenth century and early part of the twentieth, scientists discovered that atoms are composed of certain subatomic particles and that, no matter what the element, the same subatomic particles make up the atom. The number of the various subatomic particles is the only thing that varies.

Scientists now recognize that there are many subatomic particles (this really makes physicists salivate). But in order to be successful in chemistry, you really only need to be concerned with the three major subatomic particles:

ü Protons

ü Neutrons

ü Electrons

Table 3-1 summarizes the characteristics of these three subatomic particles.

Table 3-1. The Three Major Subatomic Particles

In Table 3-1, the masses of the subatomic particles are listed in two ways: grams and amu, which stands for atomic mass units. Expressing mass in amu is much easier than using the gram equivalent.

Atomic mass units are based on something called the Carbon 12 scale, a worldwide standard that’s been adopted for atomic weights. By international agreement, a carbon atom that contains 6 protons and 6 neutrons has an atomic weight of exactly 12 amu, so 1 amu is 1/12 of this carbon atom. I know, what do carbon atoms and the number 12 have to do with anything? Just trust me. Because the mass in grams of protons and neutrons are almost exactly the same, both protons and neutrons are said to have a mass of 1 amu. Notice that the mass of an electron is much smaller than that of either a proton or neutron. It takes almost 2,000 electrons to equal the mass of a single proton.

Table 3-1 also shows the electrical charge associated with each subatomic particle. Matter can be electrically charged in one of two ways: positive or negative. The proton carries one unit of positive charge, the electron carries one unit of negative charge, and the neutron has no charge — it’s neutral.

REMEMBER. Scientists have discovered through observation that objects with like charges, whether positive or negative, repel each other, and objects with unlike charges attract each other.

The atom itself has no charge. It’s neutral. (Well, actually, Chapter 6 explains that certain atoms can gain or lose electrons and acquire a charge. Atoms that gain a charge, either positive or negative, are called ions.) So how can an atom be neutral if it contains positively charged protons and negatively charged electrons? Ah, good question. The answer is that there are equal numbers of protons and electrons — equal numbers of positive and negative charges — so they cancel each other out.

The last column in Table 3-1 lists the location of the three subatomic particles. Protons and neutrons are located in the nucleus, a dense central core in the middle of the atom, while the electrons are located outside the nucleus (see “Where Are Those Electrons?” later in this chapter).

The Nucleus: Center Stage

In 1911, Ernest Rutherford discovered that atoms have a nucleus — a center — containing protons. Scientists later discovered that the nucleus also houses the neutron.

The nucleus is very, very small and very, very dense when compared to the rest of the atom. Typically, atoms have diameters that measure around 10^-10 meters. (That’s small!) Nuclei are around 10'¹⁵ meters in diameter. (That’s really small!) For example, if the Superdome in New Orleans represented a hydrogen atom, the nucleus would be about the size of a pea.

The protons of an atom are all crammed together inside the nucleus. Now some of you may be thinking, “Okay, each proton carries a positive charge, and like charges repel each other. So if all the protons are repelling each other, why doesn’t the nucleus simply fly apart?” It’s The Force, Luke. Forces in the nucleus counteract this repulsion and hold the nucleus together. (Physicists call these forces nuclear glue. But sometimes this “glue” isn’t strong enough, and the nucleus does break apart. This process is called radioactivity.)

Not only is the nucleus very small, but it also contains most of the mass of the atom. In fact, for all practical purposes, the mass of the atom is the sum of the masses of the protons and neutrons. (I ignore the minute mass of the electrons unless I’m doing very, very precise calculations.)

The sum of the number of protons plus the number of neutrons in an atom is called the mass number. And the number of protons in a particular atom is given a special name, the atomic number. Chemists commonly use the symbolization shown in Figure 3-1 to represent these things for a particular element.

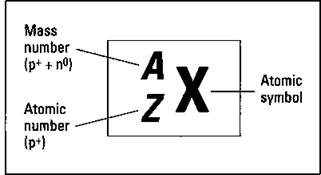
Figure 3-1: Representing a specific element.

As shown in Figure 3-1, chemists use the placeholder X to represent the chemical symbol. You can find an element’s chemical symbol on the periodic table or a list of elements (see Table 3-2 for a list of elements). The placeholder Z represents the atomic number — the number of protons in the nucleus. And A represents the mass number, the sum of the number of protons plus neutrons. The mass number (also called the atomic weight) is listed in amu.

Suppose you want to represent uranium. You can refer to a periodic table or a list of elements, such as the one shown in Table 3-2, and find that the symbol for uranium is U, its atomic number is 92, and its mass number is 238.

Table 3-2. The Elements

So you can represent uranium as shown in Figure 3-2.

Figure 3-2: Representing uranium.

You know that uranium has an atomic number of 92 (number of protons) and mass number of 238 (protons plus neutrons). So if you want to know the number of neutrons in uranium, all you have to do is subtract the atomic number (92 protons) from the mass number (238 protons plus neutrons). The resulting number shows that uranium has 146 neutrons.

But how many electrons does uranium have? Because the atom is neutral (it has no electrical charge), there must be equal numbers of positive and negative charges inside it, or equal numbers of protons and electrons. So there are 92 electrons in each uranium atom.

Where Are Those Electrons?

Early models of the atom had electrons spinning around the nucleus in a random fashion. But as scientists learned more about the atom, they found that this representation probably wasn’t accurate. Today, two models of atomic structure are used: the Bohr model and the quantum mechanical model. The Bohr model is simple and relatively easy to understand; the quantum mechanical model is based on mathematics and is more difficult to understand. Both, though, are helpful in understanding the atom, so I explain each in the following sections (without resorting to a lot of math).

REMEMBER. A model is useful because it helps you understand what’s observed in nature. It’s not unusual to have more than one model represent and help people understand a particular topic.

The Bohr model — it's really not boring

Have you ever bought color crystals for your fireplace — to make flames of different colors? Or have you ever watched fireworks and wondered where the colors came from?

Color comes from different elements. If you sprinkle table salt — or any salt containing sodium — on a fire, you get a yellow color. Salts that contain copper give a greenish-blue flame. And if you look at the flames through a spectroscope, an instrument that uses a prism to break up light into its various components, you see a number of lines of various colors. Those distinct lines of color make up a line spectrum.

Niels Bohr, a Danish scientist, explained this line spectrum while developing a model for the atom.

The Bohr model shows that the electrons in atoms are in orbits of differing energy around the nucleus (think of planets orbiting around the sun). Bohr used the term energy levels (or shells') to describe these orbits of differing energy. And he said that the energy of an electron is quantized, meaning electrons can have one energy level or another but nothing in between.

The energy level an electron normally occupies is called its ground state. But it can move to a higher-energy, less-stable level, or shell, by absorbing energy. This higher-energy, less-stable state is called the electron’s excited state.

After it’s done being excited, the electron can return to its original ground state by releasing the energy it has absorbed (see Figure 3-3). And here’s where the line spectrum explanation comes in. Sometimes the energy released by electrons occupies the portion of the electromagnetic spectrum (the range of wavelengths of energy) that humans detect as visible light. Slight variations in the amount of the energy is seen as light of different colors.

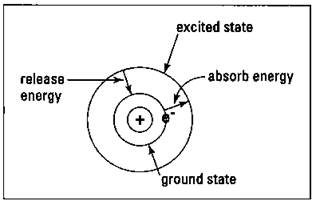
Figure 3-3: Ground and excited states in the Bohr model.

Bohr found that the closer an electron is to the nucleus, the less energy it needs, but the farther away it is, the more energy it needs. So Bohr numbered the electron’s energy levels. The higher the energy-level number, the farther away the electron is from the nucleus — and the higher the energy.

Bohr also found that the various energy levels can hold differing numbers of electrons: energy level 1 may hold up to 2 electrons, energy level 2 may hold up to 8 electrons, and so on.

The Bohr model worked well for very simple atoms such as hydrogen (which has 1 electron) but not for more complex atoms. Although the Bohr model is still used today, especially in elementary textbooks, a more sophisticated (and complex) model — the quantum mechanical model — is used much more frequently.

Quantum mechanical model

The simple Bohr model was unable to explain observations made on complex atoms, so a more complex, highly mathematical model of atomic structure was developed — the quantum mechanical model.

This model is based on quantum theory, which says matter also has properties associated with waves. According to quantum theory, it’s impossible to know the exact position and momentum (speed and direction) of an electron at the same time. This is known as the Uncertainty Principle. So scientists had to replace Bohr’s orbits with orbitals (sometimes called electron clouds), volumes of space in which there is likely to be an electron. In other words, certainty was replaced with probability.

The quantum mechanical model of the atom uses complex shapes of orbitals rather than Bohr’s simple circular orbits. Without resorting to a lot of math (you’re welcome), this section shows you some aspects of this newest model of the atom.

Four numbers, called quantum numbers, were introduced to describe the characteristics of electrons and their orbitals. You’ll notice that they were named by totally top-rate techno-geeks:

ü Principal quantum number n

ü Angular momentum quantum number l

ü Magnetic quantum number m_l

ü Spin quantum number m_s

Table 3-3 summarizes the four quantum numbers. When they’re all put together, theoretical chemists have a pretty good description of the characteristics of a particular electron.

Table 3-3. Summary of the Quantum Numbers

The principal quantum number n

The principal quantum number n describes the average distance of the orbital from the nucleus — and the energy of the electron in an atom. It’s really about the same as Bohr’s energy-level numbers. It can have positive integer (whole number) values: 1, 2, 3,4, and so on. The larger the value of n, the higher the energy and the larger the orbital. Chemists sometimes call the orbitals electron shells.

The angular momentum quantum number l

The angular momentum quantum number l describes the shape of the orbital, and the shape is limited by the principal quantum number n: The angular momentum quantum number / can have positive integer values from 0 to n-1. For example, if the n value is 3, three values are allowed for l: 0, 1, and 2.

REMEMBER. The value of l defines the shape of the orbital, and the value of n defines the size.

Orbitals that have the same value of n but different values of l are called subshells. These subshells are given different letters to help chemists distinguish them from each other. Table 3-4 shows the letters corresponding to the different values of l.

Table 3-4. Letter Designation of the Subshells

When chemists describe one particular subshell in an atom, they can use both the n value and the subshell letter — 2p, 3d, and so on. Normally, a subshell value of 4 is the largest needed to describe a particular subshell. If chemists ever need a larger value, they can create subshell numbers and letters.

Figure 3-4 shows the shapes of the s, p, and d orbitals.

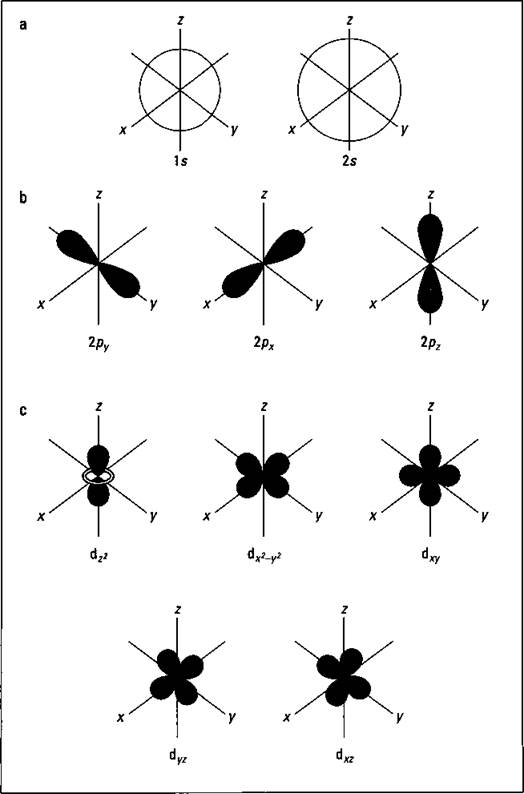
Figure 3-4: Shapes of the s, p, and d orbitals.

In Figure 3-4 (a), there are two s orbitals — one for energy level 1 (1s) and the other for energy level 2 (2s). S orbitals are spherical with the nucleus at the center. Notice that the 2s orbital is larger in diameter than the Is orbital. In large atoms, the 1s orbital is nestled inside the 2s, just like the 2p is nestled inside the 3p.

Figure 3-4 (b) shows the shapes of the p orbitals, and Figure 3-4 (c) shows the shapes of the d orbitals. Notice that the shapes get progressively more complex.

The magnetic quantum number m_l

The magnetic quantum number m_l describes how the various orbitals are oriented in space. The value of depends on the value of l. The values allowed are integers from -l to 0 to +l. For example, if the value of l = 1 (p orbital — see Table 3-4), you can write three values for m_l: -1, 0, and +1. This means that there are three different p subshells for a particular orbital. The subshells have the same energy but different orientations in space.

Figure 3-4 (b) shows how the p orbitals are oriented in space. Notice that the three p orbitals correspond to m_{ values of -1, 0, and +1, oriented along the x, y, and z axes.

The spin quantum number m_s

The fourth and final (I know you’re glad — techie stuff, eh?) quantum number is the spin quantum number m_s. This one describes the direction the electron is spinning in a magnetic field — either clockwise or counterclockwise. Only two values are allowed for m_s: +1/2 or -1/2. For each subshell, there can be only two electrons, one with a spin of +1/2 and another with a spin of -1/2.

Put alt the numbers together and whaddya get) (A pretty table)

I know. Quantum number stuff makes science nerds drool and normal people yawn. But, hey, sometime if the TV’s on the blink and you’ve got some time to kill, take a peek at Table 3-5. You can check out the quantum numbers for each electron in the first two energy levels (oh boy, oh boy, oh boy).

Table 3-5. Quantum Numbers for the First Two Energy Levels

Table 3-5 shows that in energy level 1 (n=1) there’s only an s orbital. There’s no p orbital because an l value oil (p orbital) is not allowed. And notice that there can be only two electrons in that Is orbital (m_s of +1/2 and -1/2). In fact, there can be only two electrons in any s orbital, whether it’s Is or 5s.

When you move from energy level 1 to energy level 2 (n=2), there can be both s and p orbitals. If you write out the quantum numbers for energy level 3, you see s, p, and d orbitals. Each time you move higher in a major energy level, you add another orbital type.

Notice also that there are three subshells (m/) for the 2p orbital (see Figure 3-4 (b)) and that each holds a maximum of two electrons. The three 2p subshells can hold a maximum of six electrons.

There’s an energy difference in the major energy levels (energy level 2 is higher in energy than energy level 1), but there’s also a difference in the energies of the different orbitals within an energy level. At energy level 2, both s and p orbitals are present. But the 2s is lower in energy than the 2p. The three subshells of the 2p orbital have the same energy. Likewise, the five subshells of the d orbitals (see Figure 34 (c)) have the same energy.

Okay. Enough already.

Electron configurations (Bed Check for Electrons)

Chemists find quantum numbers useful when they’re looking at chemical reactions and bonding (and those are things many chemists like to study).

But they find two other representations for electrons more useful and easier to work with:

ü Energy level diagrams

ü Electron configurations

Chemists use both of these things to represent which energy level, subshell, and orbital are occupied by electrons in any particular atom. Chemists use this information to predict what type of bonding will occur with a particular element and show exactly which electrons are being used. These representations are also useful in showing why certain elements behave in similar ways. In this section, I show you how to use an energy level diagram and write electron configurations.

The dreaded energy level diagram

Figure 3-5 is a blank energy level diagram you can use to depict electrons for any particular atom. Not all the known orbitals and subshells are shown. But with this diagram, you should be able to do most anything you need to. (If you don’t have a clue what orbitals, subshells, or all those numbers and letters in the figure have to do with the price of beans, check out the “Quantum mechanical model” section, earlier in this chapter. Fun read, lemme tell ya.)

I represent orbitals with dashes in which you can place a maximum of two electrons. The Is orbital is closest to the nucleus, and it has the lowest energy. It’s also the only orbital in energy level 1 (refer to Table 3-5). At energy level 2, there are both s and p orbitals, with the 2s having lower energy than the 2p. The three 2p subshells are represented by three dashes of the same energy. Energy levels 3, 4, and 5 are also shown. Notice that the 4s has lower energy than the 3d: This is an exception to what you may have thought, but it’s what’s observed in nature. Go figure. Speaking of which, Figure 3-6 shows the Aufbau Principle, a method for remembering the order in which orbitals fill the vacant energy levels.

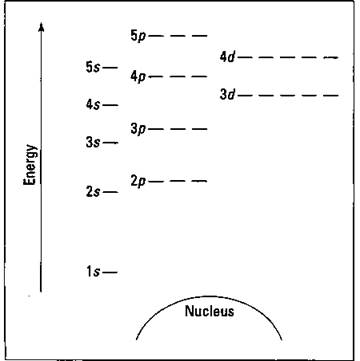
Figure 3-5: Energy level diagram.

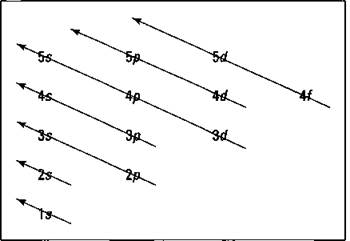
Figure 3-6: Aufbau filling chart.

REMEMBER. In using the energy level diagram, remember two things:

ü Electrons fill the lowest vacant energy levels first.

ü When there’s more than one subshell at a particular energy level, such as at the 3p or 4d levels (see Figure 3-5), only one electron fills each subshell until each subshell has one electron. Then electrons start pairing up in each subshell. This rule is named Hund’s Rule.

Suppose you want to draw the energy level diagram of oxygen. You look on the periodic table or an element list and find that oxygen is atomic number 8. This number means that oxygen has 8 protons in its nucleus and 8 electrons. So you put 8 electrons into your energy level diagram. You can represent electrons as arrows (see Figure 3-7). Note that if two electrons end up in the same orbital, one arrow faces up and the other faces down. (This is called spin pairing. It corresponds to the +1/2 and -1/2 of m_s. — see “The spin quantum number m_s” section earlier in this chapter.)

The first electron goes into the 1s orbital, filling the lowest energy level first, and the second one spin pairs with the first one. Electrons 3 and 4 spin pair in the next lowest vacant orbital — the 2s. Electron 5 goes into one of the 2p subshells (no, it doesn’t matter which one — they all have the same energy), and electrons 6 and 7 go into the other two totally vacant 2p orbitals (see the two things you’re supposed to remember about the energy level diagram, a little ways back from here). The last electron spin pairs with one of the electrons in the 2p subshells (again, it doesn’t matter which one you pair it with). Figure 3-7 shows the completed energy level diagram for oxygen.

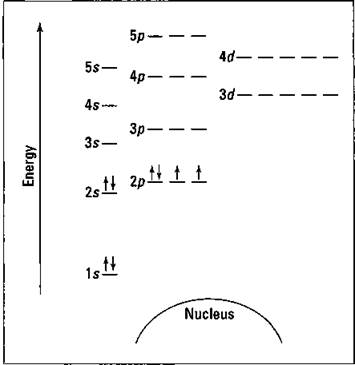
Figure 3-7: Energy level diagram for oxygen.

Electron configurations: Easy and space efficient

Energy level diagrams are useful when you need to figure out chemical reactions and bonding, but they’re very bulky to work with. Wouldn’t it be nice if there were another representation that gives just about the same information but in a much more concise, shorthand-notation form? Well, there is. It’s called the electron configuration.

The electron configuration for oxygen is 1s²2s²2p⁴. Compare that notation with the energy level diagram for oxygen in Figure 3-7. Doesn’t the electron configuration take up a lot less space? You can derive the electron configuration from the energy level diagram. The first two electrons in oxygen fill the Is orbital, so you show it as 1s² in the electron configuration. The 1 is the energy level, the s represents the type of orbital, and the superscript 2 represents the number of electrons in that orbital. The next two electrons are in the 2s orbital, so you write 2s². And, finally, you show the 4 electrons in the 2p orbital as 2p⁴. Put it all together, and you get 1s²2s²2p⁴.

Some people use a more expanded form, showing how the individual p_x, p_y, and p_z orbitals are oriented along the x, y, and z axes and the number of electrons in each orbital. (The section “The magnetic quantum number m_l” earlier in this chapter, explains how orbitals are oriented in space.) The expanded form is nice if you’re really looking at the finer details, but most of the time you won’t need that amount of detail in order to show bonding situations and such, so I’m not going to explain the expanded form here.

TIP. The sum of the superscript numbers equals the atomic number, or the number of electrons in the atom.

Here are a couple of electron configurations you can use to check your conversions from energy level diagrams:

Chlorine (Cl): 1s²2s²2p⁶3s²3p⁵

Iron (Fe): 1s²2s²2p⁶3s²3p⁶4s²3d⁶

Although I’ve showed you how to use the energy level diagram to write the electron configuration, with a little practice, you can omit doing the energy level diagram altogether and simply write the electron configuration by knowing the number of electrons and the orbital filling pattern. Anything to save a little precious time, right?

Valence electrons: Lilting on the edge

When chemists study chemical reactions, they study the transfer or sharing of electrons. The electrons more loosely held by the nucleus — the electrons in the energy level farthest away from the nucleus — are the ones that are gained, lost, or shared.

REMEMBER. Electrons are negatively charged, while the nucleus has a positive charge due to the protons. The protons attract and hold the electrons, but the farther away the electrons are, the less the attractive force.

The electrons in the outermost energy level are commonly called valence electrons. Chemists really only consider the electrons in the s and p orbitals in the energy level that is currently being filled as valence electrons. In the electron configuration for oxygen, 1s²2s²2p⁴, energy level 1 is filled, and there are 2 electrons in the 2s orbital and 4 electrons in the 2p orbital for a total of 6 valence electrons. Those valence electrons are the ones lost, gained, or shared.

Being able to determine the number of valence electrons in a particular atom gives you a big clue as to how that atom will react. In Chapter 4, which gives an overview of the periodic table, I show you a quick way to determine the number of valence electrons without writing the electron configuration of the atom.

Isotopes and Ions: These Are a Few of My Favorite Things

But then again, I’m a nerd. The atoms in a particular element have an identical number of protons and electrons but can have varying numbers of neutrons. If they have different numbers of neutrons, then the atoms are called isotopes.

Isolating the isotope

Hydrogen is a common element here on earth. Hydrogen’s atomic number is 1 — its nucleus contains 1 proton. The hydrogen atom also has 1 electron. Because it has the same number of protons as electrons, the hydrogen atom is neutral (the positive and negative charges have canceled each other out).

Most of the hydrogen atoms on earth contain no neutrons. You can use the symbolization shown in Figure 3-2 to represent hydrogen atoms that don’t contain neutrons, as shown in Figure 3-8 (a).

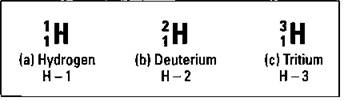
Figure 3-8: The isotopes of hydrogen.

However, approximately one hydrogen atom out of 6,000 contains a neutron in its nucleus. These atoms are still hydrogen, because they have one proton and one electron; they simply have a neutron that most hydrogen atoms lack. So these atoms are called isotopes. Figure 3-8 (b) shows an isotope of hydrogen, commonly called deuterium. It’s still hydrogen, because it contains only one proton, but it’s different from the hydrogen in Figure 3-8 (a), because it also has one neutron. Because it contains one proton and one neutron, its mass number is two.

There’s even an isotope of hydrogen containing two neutrons. This one’s called tritium, and it’s represented in Figure 3-8 (c). Tritium doesn’t occur naturally on earth, but it can easily be created.

Now take another look at Figure 3-8. It also shows an alternative way of representing isotopes: Write the element symbol, a dash, and then the mass number.

Now you may be wondering, “If I’m doing a calculation involving the atomic mass of hydrogen, which isotope do I use?” Well, you use an average of all the naturally occurring isotopes of hydrogen. But not a simple average. (You have to take into consideration that there’s a lot more H-1 than H-2, and you don’t even consider H-3, because it’s not naturally occurring.) You use a weighted average, which takes into consideration the abundances of the naturally occurring isotopes. That’s why the atomic mass of hydrogen in Table 3-2 isn’t a whole number: It’s 1.0079 amu. The number shows that there’s a lot more H-1 than H-2.

Many elements have severed isotopic forms. You can find out more about them in Chapter 5.

Keeping an eye on ions

Because an atom itself is neutral, throughout this book I say that the number of protons and electrons in atoms are equal. But there are cases in which an atom can acquire an electrical charge. For example, in the compound sodium chloride — table salt — the sodium atom has a positive charge and the chlorine atom has a negative charge. Atoms (or groups of atoms) in which there are unequal numbers of protons and electrons are called ions.

The neutral sodium atom has 11 protons and 11 electrons, which means it has 11 positive charges and 11 negative charges. Overall, the sodium atom is neutral, and it’s represented like this: Na. But the sodium ion contains one more positive charge than negative charge, so it’s represented like this: Na⁺ (the⁺ represents its net positive electrical charge).

This unequal number of negative and positive charges can occur in one of two ways: An atom can gain a proton (a positive charge) or lose an electron (a negative charge). So which process is more likely to occur? Well, a rough guideline says that it’s easy to gain or lose electrons but very difficult to gain or lose protons.

So atoms become ions by gaining or losing electrons. And ions that have a positive charge are called cations. The progression goes like this: The Na⁺ ion is formed from the loss of one electron. Because it lost an electron, it has more protons than electrons, or more positive charges than negative charges, which means it’s now called the Na⁺ cation. Likewise, The Mg²⁺ cation is formed when the neutral magnesium atom loses two electrons.

Now consider the chlorine atom in sodium chloride. The neutral chlorine atom has acquired a negative charge by gaining an electron. Because it has unequal numbers of protons and electrons, it’s now an ion, represented like this: Cl'. And because ions that have a negative charge are called anions, it’s now called the Cl" anion. (You can get the full scoop on ions, cations, and anions in Chapter 6, if you’re interested. This here’s just a teaser.)

Just for kicks, here are some extra tidbits about ions for your reading pleasure:

ü You can write electron configurations and energy level diagrams for ions. The neutral sodium atom (11 protons) has an electron configuration of 1s²2s²2p⁶3s¹. The sodium cation has lost an electron — the valence electron, which is farthest away from the nucleus (the 3s electron, in this case). The electron configuration of Na⁺ is 1s²2s²2p⁶.

ü The electron configuration of the chloride ion (Cl) is 1s²2s²2p⁶3s²3p⁶. This is the same electron configuration as the neutral Argon atom. If two chemical species have the same electron configuration, they’re said to be isoelectronic. Figuring out chemistry requires learning a whole new language, eh?

ü This section has been discussing monoatomic (one atom) ions. But polyatomic (many atom) ions do exist. The ammonium ion, NH₄⁺, is a polyatomic ion, or, specifically, a polyatomic cation. The nitrate ion, NO₃^-, is also a polyatomic ion, or, specifically, a polyatomic anion.

ü Ions are commonly found in a class of compounds called salts, or ionic solids. Salts, when melted or dissolved in water, yield solutions that conduct electricity. A substance that conducts electricity when melted or dissolved in water is called an electrolyte. Table salt — sodium chloride — is a good example. On the other hand, when table sugar (sucrose) is dissolved in water, it becomes a solution that doesn’t conduct electricity. So sucrose is a nonelectrolyte. Whether a substance is an electrolyte or a nonelectrolyte gives clues to the type of bonding in the compound. If the substance is an electrolyte, the compound is probably ionically bonded (see Chapter 6). If it’s a nonelectrolyte, it’s probably covalently bonded (see Chapter 7).