Chemistry Essentials for Dummies

Chapter 8. Electrochemistry: Using Electrons

Balancing Redox Equations

Redox equations are often so complex that the inspection method (the fiddling-with-coefficients method) of balancing chemical equations doesn’t work well with them. (See Chapter 7 for a discussion of this balancing method.) So chemists developed other methods of balancing redox equations, such as the ion electron (half-reaction) method.

Here’s an overview of how it works: You convert the unbalanced redox equation to the ionic equation and then break it down into two half-reactions — oxidation and reduction. Balance each of these half-reactions separately and then combine them to give the balanced ionic equation. Finally, put the spectator ions into the balanced ionic equation, converting the reaction back to the molecular form. (For a discussion of molecular, ionic, and net-ionic equations, see Chapter 7.)

To successfully balance redox equations with the ion electron method, you need to follow the steps precisely and in order. Here’s what to do:

1. Convert the unbalanced redox reaction to the ionic form.

Suppose you want to balance this redox equation:

In this reaction, you show the nitric acid in the ionic form, because it’s a strong acid (for a discussion of strong acids, see Chapter 11). Copper(II) nitrate is soluble (indicated by (aq)), so show it in its ionic form (see Chapter 7). Because NO(g) and water are molecular compounds, they remain in the molecular form:

2. If necessary, assign oxidation numbers; then write two half-reactions (oxidation and reduction) that show the chemical species that have had their oxidation numbers changed.

In some cases, telling what’s been oxidized and reduced is easy; in other cases, it isn’t. Start by going through the example reaction and assigning oxidation numbers (see the earlier section “Oxidation numbers” for details):

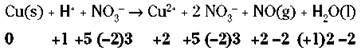
To write your half-reactions, look closely for places where the oxidation numbers have changed, and write down those chemical species. Copper changes its oxidation number (from 0 to 2) and so does nitrogen (from -5 to +2), so your unbalanced half-reactions are

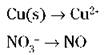
3. Balance all atoms, with the exception of oxygen and hydrogen.

Starting with the two unbalanced half-reactions above, you can balance atoms other than oxygen and hydrogen by inspection — fiddling with the coefficients. (You can’t change subscripts; you can only add coefficients.) In this case, both the copper and nitrogen atoms already balance, with one each on both sides:

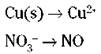
4. Balance the oxygen atoms.

How you balance these atoms depends on whether you’re dealing with acid or basic solutions:

· In acidic solutions, take the number of oxygen atoms needed and add that same number of water molecules to the side that needs oxygen.

· In basic solutions, add two OH^- to the side that needs oxygen for every oxygen atom that is needed. Then, to the other side of the equation, add half as many water molecules as OH^- anions used.

An acidic solution shows some acid or H+; a basic solution has an OH^- present. The example equation is in acidic conditions (nitric acid, HNO₃, which is H+ + NO₃^- in ionic form). You don’t have to do anything on the half-reaction involving the copper, because no oxygen atoms are present. But you do need to balance the oxygen atoms in the second half-reaction:

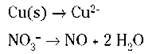
5. Balance the hydrogen atoms.

Again, how you balance these atoms depends on whether you’re dealing with acid or basic solutions:

· In acidic solutions, take the number of hydrogen atoms needed and add that same number of H⁺ to the side that needs hydrogen.

· In basic solutions, add one water molecule to the side that needs hydrogen for every hydrogen atom that’s needed. Then, to the other side of the equation, add as many OH^- anions as water molecules used.

The example equation is in acidic conditions. You need to balance the hydrogen atoms in the second half-reaction:

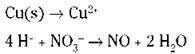
6. Balance the ionic charge on each half-reaction by adding electrons.

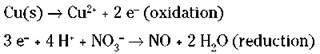
The electrons should end up on opposite sides of the equation in the two half-reactions. Remember that you’re using ionic charge, not oxidation numbers.

7. Balance electron loss with electron gain between the two half-reactions.

The electrons that are lost in the oxidation halfreaction are the same electrons that are gained in the reduction half-reaction, so the number of electrons lost and gained must be the same. But Step 6 shows a loss of two electrons and a gain of three. So you must adjust the numbers using appropriate multipliers for both half-reactions. In this case, you have to find the lowest common multiple of 2 and 3. It’s 6, so multiply the first half-reaction by 3 and the second half-reaction by 2.

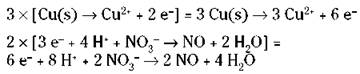
8. Add the two half-reactions together and cancel anything common to both sides.

REMEMBER. The electrons should always cancel (the number of electrons should be the same on both sides).

9. Convert the equation back to the molecular form by adding the spectator ions.

If it’s necessary to add spectator ions (ions not involved in the reaction, but there to ensure electrical neutrality - Chapter 7) to one side of the equation in order to convert it back to the molecular equation, add the same number to the other side of the equation. For example, there are eight H⁺ on the left side of the equation. In the original equation, the H+ was in the molecular form of HNO₃. You need to add the NO₃^- spectator ions back to it. You already have 2 on the left, so simply add 6 more. You then add 6 NO₃^- to the right-hand side to keep things balanced. Those are the spectator ions that you need for the Cu²⁺ cation to convert it back to the molecular form that you want.

10. Check to make sure that all the atoms are balanced, all the charges are balanced (if working with an ionic equation at the beginning), and all the coefficients are in the lowest whole-number ratio.

That’s how it’s done. Reactions that take place in bases are just as easy, as long as you follow the rules.