Chemistry Essentials for Dummies
Chapter 10. A Salute to Solutions
Understanding Solution Concentration Units
People need to have a quantitative method to describe the relative amount of solute and solvent in a solution. For instance, consider the case of IV solutions — they must have a very precise amount of solute in them, or the patient will be in danger. Chemists use solution concentration units to quantify solutes and solvents.
You can use a variety of solution concentration units to quantitatively describe the relative amounts of the solute(s) and the solvent. In everyday life, percentage is commonly used. In chemistry, molarity (the moles of solute per liter of solution) is the solution concentration unit of choice. In certain circumstances, though, another unit, molality (the moles of solute per kilogram of solvent), is used. And I use parts-per-million or parts-per-billion when I discuss pollution control. The following sections cover these concentration units.
Percent composition
You’ve probably seen labels like “5% acetic acid” on a bottle of vinegar, “3% hydrogen peroxide” on a bottle of hydrogen peroxide, or “5% sodium hypochlorite” on a bottle of bleach. Those percentages are expressing the concentration of that particular solute in each solution. Percentage is the amount per 100. Depending on the way you choose to express the percentage, the units of amount per one hundred vary. Three different percentages are commonly used:
✓ Weight/weight (w/w) percentage
✓ Weight/volume (w/v) percentage
✓ Volume/volume (v/v) percentage
Unfortunately, although the percentage of solute is often listed, the method (w/w, w/v, v/v) is not. In this case, I normally assume that the method is weight/weight, but I’m sure you know about assumptions.
Most of the solutions I talk about in the following examples of these percentages are aqueous solutions, solutions in which water is the solvent.
Weight/weight percentage
In weight/weight percentage, or weight percentage, the weight of the solute is divided by the weight of the solution and then multiplied by 100 to get the percentage. Normally, the weight unit is grams. Mathematically, it looks like this:
![]()
If, for example, you dissolve 5.0 grams of sodium chloride in 45 grams of water, the weight percent is
![]()
Therefore, the solution is a 10 percent (w/w) solution.
Weight percentage is the easiest percentage solution to make. Suppose that you want to make 350.0 grams of a 5 percent (w/w) sucrose (table sugar) solution. You know that 5 percent of the weight of the solution is sugar, so you can multiply the 350.0 grams by 0.05 to get the weight of the sugar:
350.0 grams x 0.05 = 17.5 grams of sugar
The rest of the solution (350.0 grams - 17.5 grams = 332.5 grams) is water. You can simply weigh out 17.5 grams of sugar and add it to 332.5 grams of water to get your 5 percent (w/w) solution.
Weight/Volume percentage
Weight/volume percentage is very similar to weight/weight percentage, but instead of using grams of solution in the denominator, it uses milliliters of solution:
![]()
Suppose that you want to make 100 milliliters of a 15 percent (w/v) potassium nitrate solution. Because you’re making 100 milliliters, you already know that you’re going to weigh out 15 grams of potassium nitrate (commonly called saltpeter — KNO3).
Now, here comes something that’s a little different: You’re more concerned with the final volume of the solution than the amount of solvent you use. So you dissolve the 15 grams of KNO3 in a little bit of water and dilute it to exactly 100 milliliters in a volumetric flask. In other words, you dissolve and dilute 15 grams of KNO3 to 100 milliliters. (I tend to abbreviate dissolve and dilute by writing d & d.) You won’t know exactly how much water you put in, but it’s not important as long as the final volume is 100 milliliters.
You can also use the percentage and volume to calculate the grams of solute present. You may want to know how many grams of sodium hypochlorite are in 500 milliliters of a 5 percent (w/v) solution of household bleach. You can set up the problem like this:
![]()
You now know that you have 25 grams of sodium hypochlorite in the 500 milliliters of solution.
Volume/volume percentage
If both the solute and solvent are liquids, using a volume/ volume percentage is convenient. With volume/volume percentages, both the solute and solution are expressed in milliliters:
![]()
Ethyl alcohol (the drinking alcohol) solutions are commonly made using volume/volume percentages. If you want to make 100 milliliters of a 50 percent ethyl alcohol solution, you take 50 milliliters of ethyl alcohol and dilute it to 100 milliliters with water. Again, it’s a case of dissolving and diluting to the required volume.
You can’t simply add 50 milliliters of alcohol to 50 milliliters of water — you’d get less than 100 milliliters of solution. The polar water molecules attract the polar alcohol molecules. This tends to fill in the open framework of water molecules and prevents the volumes from simply being added together.
Molarity: Comparing solute to solution
Molarity is the concentration unit chemists use most often, because it utilizes moles. The mole concept is central to chemistry, and molarity lets chemists easily work solutions into reaction stoichiometry. (If you’re wondering what burrowing, insect-eating mammals have to do with chemistry, let alone what stoichiometry is, just flip to Chapter 9 for the scoop.)
Molarity (M) is defined as the moles of solute per liter of solution. Mathematically, it looks like this:
![]()
For example, you can take 1 mole (abbreviated as mol) of KCl (formula weight of 74.55 g/mol; see Chapter 10) and dissolve and dilute the 74.55 grams to 1 liter of solution in a volumetric flask. You then have a 1-molar solution of KCl. You can label that solution as 1 M KCl.
REMEMBER. When preparing molar solutions, always dissolve and dilute to the required volume. So to dissolve 74.55 grams of KCl to 1 liter of solution, you don’t add the 74.55 grams to 1 liter of water. You want to end up with a final volume of 1 liter.
Here’s another example: If 25.0 grams of KCl are dissolved and diluted to 350.0 milliliters, how would you calculate the molarity of the solution? You know that molarity is moles of solute per liter of solution. So you can take the grams, convert them to moles using the formula weight of KCl (74.55 g/mol), and divide them by 0.350 liters (350.0 milliliters). You can set up the equation like this:
![]()
Now suppose that you want to prepare 2.00 liters of a 0.550 M KCl solution. The first thing you do is calculate how much KCl you need to weigh:
![]()
You then take that 82.0 grams of KCl and dissolve and dilute it to 2.00 liters.
Diluting solutions to the right molarity
There’s one more way to prepare solutions — the dilution of a more concentrated solution to a less-concentrated one. For example, you can buy hydrochloric acid from the manufacturer as a concentrated solution of 12.0 M. Suppose that you want to prepare 500 milliliters of 2.0 M HCl. You can dilute some of the 12.0 M to 2.0 M, but how much of the 12.0 M HCl do you need? You can easily figure the volume (V) you need by using the following formula:
![]()
In the preceding equation, Ko|d is the old volume, or the volume of the original solution, Mold is the molarity of the original solution, Knew is the volume of the new solution, and Mnew is the molarity of the new solution. After substituting the values, you have the following:
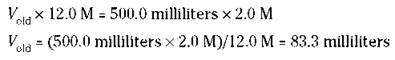
You then take 83.3 milliliters of the 12.0 M HCl solution and dilute it to exactly 500.0 milliliters.
If you’re actually doing a dilution of concentrated acids, be sure to add the acid to the water instead of the other way around! If the water is added to the concentrated acid, then so much heat will be generated that the solution will quite likely splatter all over you. So to be safe, you should take about 400 milliliters of water, slowly add the 83.3 milliliters of the concentrated HCl as you stir, and then dilute to the final 500 milliliters with water.
Molarity in stoichiometry: Figuring out how much you need
The usefulness of the molarity concentration unit is readily apparent when dealing with reaction stoichiometry. For example, suppose that you want to know how many milliliters of 2.50 M sulfuric acid it takes to neutralize a solution containing 100.0 grams of sodium hydroxide. The first thing you must do is write the balanced chemical equation for the reaction:
![]()
You know that you have to neutralize 100.0 grams of NaOH. You can convert the weight to moles (using the formula weight of NaOH, 40.00 g/mol) and then convert from moles of NaOH to moles of H2SO4. Then you can use the molarity of the acid solution to get the volume:

It takes 500.0 milliliters of the 2.50 M H2SO4 solution to completely react with the solution that contains 100 grams of NaOH.
Molality: Comparing solute to solvent
Molality is another concentration term that involves moles of solute. It isn’t used very much, but you may happen to run across it. Molality (m) is defined as the moles of solute per kilogram of solvent. It’s one of the few concentration units that doesn’t use the total solution’s weight or volume. Mathematically, it looks like this:
![]()
Suppose, for example, you want to dissolve 15.0 grams of NaCl in 50.0 grams of water. You can calculate the molality like this (you must convert the 50.0 grams to kilograms before you use it in the equation):
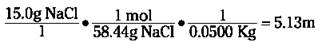
Parts per million
Percentage and molarity, and even molality, are convenient units for the solutions that chemists routinely make in the lab or the solutions commonly found in nature. However, if you begin to examine the concentrations of certain pollutants in the environment, you find that those concentrations are very, very small. Percentage and molarity work when you’re measuring solutions in the environment, but they’re not very convenient. To express the concentrations of very dilute solutions, scientists have developed another concentration unit — parts per million.
Percentage is parts per hundred, or grams solute per 100 grams of solution. Parts per million (ppm) is grams of solute per 1 million grams of solution — or as it’s most commonly expressed, milligrams of solute per kilogram of solution, which is the same ratio. It’s expressed this way because chemists can easily weigh out milligrams or even tenths of milligrams, and if you’re talking about aqueous solutions, a kilogram of solution is the same as a liter of solution. (The density of water is 1 gram per milliliter, or 1 kilogram per liter. The weight of the solute in these solutions is so very small that it’s negligible when converting from the mass of the solution to the volume.)
By law, the maximum contamination level of lead in drinking water is 0.05 ppm. This number corresponds to 0.05 milligrams of lead per liter of water. That’s pretty dilute. But mercury is regulated at the 0.002 ppm level. Sometimes, even this unit isn’t sensitive enough, so environmentalists have resorted to the parts per billion (ppb) or parts per trillion (ppt) concentration units. Some neurotoxins are deadly at the parts per billion level.