Chemistry Essentials for Dummies

Chapter 11. Acids and Bases

Understanding Strong and Weak Acids and Bases

I want to introduce you to a couple of different categories of acids and bases — strong and weak. Strength refers to the amount of ionization or breaking apart that a particular acid or base undergoes.

Acid-base strength is not the same as concentration. Concentration refers to the amount of acid or base that you initially have. You can have a concentrated solution of a weak acid, or a dilute solution of a strong acid, or a concentrated solution of a strong acid or ... well, I’m sure you get the idea.

Remember, as I said previously, an acid yields hydronium ions (H₃O⁺) and a base reacts with them. Many times that base will be the hydroxide ion (OH^-). The concentrations of these acid and base ions will prove to be important to us.

Strong: Ionizing all the Way

An acid or base is strong if it ionizes completely — the reactants keep creating the product until they’re all used up. In this section, I discuss both strong acids and strong bases.

Hydrogen chloride and other strong acids

If you dissolve hydrogen chloride gas in water, the HCl reacts with the water molecules and donates a proton to them:

The H₃O⁺ ion is called the hydronium ion. This reaction goes essentially to completion. In this case, all the HCl ionizes to H₃O⁺ and Cl^- until there’s no more HCl present. Because HCl ionizes essentially 100 percent in water, it’s considered a strong acid. Note that water, in this case, acts as a base, accepting the proton from the hydrogen chloride.

Calculating ion concentration in solutions

Because strong acids ionize completely, calculating the concentration of the ions in solution is easy if you know the initial concentration of the strong acid. For example, suppose that you bubble 0.1 moles of HCl gas into a liter of water (see Chapter 9 to get a firm grip on moles). You can say that the initial concentration of HCl is 0.1 M (0.1 mol/L). M stands for molarity, and mol/L stands for moles of solute per liter. (For a detailed discussion of molarity and other concentration units, see Chapter 10.)

You can represent this 0.1 M concentration for the HCl in this fashion: [HCl] = 0.1. Here, the brackets around the compound indicate molar concentration, or mol/L. Because the HCl completely ionizes, you see from the balanced equation that for every HCl that ionizes, you get one hydronium ion and one chloride ion. So the concentration of ions in that 0.1 M HCl solution is

The relationship between the amount of acid you start with and the amount of acid or base ions you end up with is valuable when you calculate the pH of a solution. (And you can do just that in the section “Phun with the pH Scale,” later in this chapter.)

Looking at common strong acids

Table 11-2 lists the most common strong acids you’re likely to encounter. Most of the other acids you encounter are weak.

Table 11-2. Common Strong Acids

Sulfuric acid is called a diprotic acid. It can donate two protons, but only the first ionization goes 100 percent. The other acids listed in Table 11-2 are monoprotic acids, because they donate only one proton.

Strong bases: Hydroxide ions

Strong bases are those compounds that totally dissociate in water, yielding some cation and the hydroxide ion. It is the hydroxide ion that we normally refer to as the base, because it is what accepts the proton. Calculating the hydroxide ion concentration is really straightforward. Suppose that you have a 1.5 M (1.5 mol/L) NaOH solution. The sodium hydroxide, a salt, completely dissociates (breaks apart) into ions:

If you start with 1.5 mol/L NaOH, then you have the same concentration of ions:

Weak: Ionizing partially

A weak acid or base ionizes only partially. The reactants aren’t completely used up creating the products, as they are with strong acids and bases. Instead, the reactants establish equilibrium. In equilibrium systems, two exactly opposite chemical reactions — one on each side of the reaction arrow — are occurring at the same place, at the same time, with the same speed of reaction. (For a discussion of equilibrium systems, see Chapter 7.)

Acetic acid and other Weak acids

Suppose that you dissolve acetic acid (CH₃COOH) in water. It reacts with the water molecules, donating a proton and forming hydronium ions. It also establishes equilibrium, where you have a significant amount of unionized acetic acid.

TIP. The acetic acid reaction with water looks like this:

The amount of hydronium ion that you get in solutions of acids that don’t ionize completely is much less than it is with a strong acid. Acids that only partially ionize are called weak acids. In the case of acetic acid, about 5 percent ionizes, and 95 percent remains in the molecular form.

Calculating the hydronium ion concentration in weak acid solutions isn’t as straightforward as it is in strong solutions, because not all the weak acid that dissolves initially has ionized. To calculate the hydronium ion concentration, you must use the equilibrium constant expression for the weak acid. Chapter 7 covers the K_eq expression that represents the equilibrium system. For weak acid solutions, you use a modified equilibrium constant expression called the K_a — the acid ionization constant.

TIP. One way to distinguish between strong and weak acids is to look for an acid ionization constant (K_a) value. If the acid has a K_a value, then it’s weak.

Take a look at the generalized ionization of some weak acid HA:

The K_a expression for this weak acid is

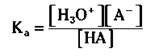
Note that the [HA] represents the molar concentration of HA at equilibrium, not initially. Also, note that the concentration of water doesn’t appear in the K_a expression, because there’s so much that it actually becomes a constant incorporated into the K_a expression.

Now go back to that acetic acid equilibrium. The K_a for acetic acid is 1.8 x 10^-5. The K_a expression for the acetic acid ionization is

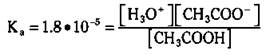
You can use this K_a when calculating the hydronium ion concentration in, say, a 2.0 M solution of acetic acid. You know that the initial concentration of acetic acid is 2.0 M. You know that a little bit has ionized, forming a little hydronium ion and acetate ion. You also can see from the balanced reaction that for every hydronium ion that’s formed, an acetate ion is also formed — so their concentrations are the same. You can represent the amount of [H₃O⁺] and [CH₃COO^-] as x, so

To produce the x amount of hydronium and acetate ion, the same amount of ionizing acetic acid is required. So you can represent the amount of acetic acid remaining at equilibrium as the amount you started with, 2.0 M, minus the amount that ionizes, x:

For the vast majority of situations, you can say that x is very small in comparison to the initial concentration of the weak acid. So you can say that 2.0 - x is approximately equal to 2.0. This means that you can often approximate the equilibrium concentration of the weak acid with its initial concentration. The equilibrium constant expression now looks like this:

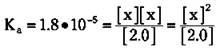
At this point, you can solve for x, which is the [H₃O⁺]:

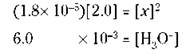
Weak bases: Ammonia

Weak bases, like weak acids, react with water to establish an equilibrium system. Ammonia is a typical weak base. It reacts with water to form the ammonium ion and the hydroxide ion:

Like a weak acid, a weak base is only partially ionized. There’s a modified equilibrium constant expression for weak bases — the K_b. You use it exactly the same way you use the K_a (see “Acetic acid and other weak acids” for the details), except you solve for the [OH^-].