Chemistry Essentials for Dummies

Chapter 12. Clearing the Air on Gases

Relating Physical Properties with Gas Laws

Various scientific laws describe the relationships between four important physical properties of gases:

✓ Volume

✓ Pressure

✓ Temperature (in Kelvin units)

✓ Amount

This section covers those various laws. Boyle’s, Charles’s, and Gay-Lussac’s laws each describe the relationship between two properties while keeping the other two properties constant; in other words, you take two properties, change one, and then see its effect on the second. Another law — a combo of Boyle’s, Charles’s, and Gay-Lussac’s individual laws — enables you to vary more than one property at a time.

That combo law doesn’t let you vary the physical property of amount. Avogadro’s Law, however, does. And there’s even an ideal gas law, which lets you take into account variations in all four physical properties.

Boyle's law: Pressure and Volume

REMEMBER. Boyle’s law (named after Robert Boyle, a 17th-century English scientist) describes the pressure-volume relationship of gases if you keep the temperature and amount of the gas constant. The law states that there’s an inverse relationship between the volume and air pressure (the collision of the gas particles with the inside walls of the container): As the volume decreases, the pressure increases, and vice versa. He determined that the product of the pressure and the volume is a constant (k):

Suppose you have a cylinder that contains a certain volume of gas at a certain pressure. When you decrease the volume, the same number of gas particles is now contained in a much smaller space, and the number of collisions increases significantly. Therefore, the pressure is greater.

Now consider a case where you have a gas at a certain pressure (P₁) and volume (V₁). If you change the volume to some new value (V₂), the pressure also changes to a new value (P₂). You can use Boyle’s Law to describe both sets of conditions:

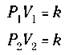
The constant, k, is going to be the same in both cases, so you can say the following, if the temperature and amount of gas don’t change:

This equation is another statement of Boyle’s Law — and it’s really a more useful one, because you normally deal with changes in pressure and volume.

If you know three of the preceding quantities, you can calculate the fourth one. For example, suppose that you have 5.00 liters of a gas at 1.00 atm pressure, and then you decrease the volume to 2.00 liters. What’s the new pressure? Use the formula. Substitute 1.00 atm for P₁, 5.00 liters for V₁, and 2.00 liters for V₂, and then solve for P₂:

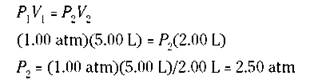
The answer makes sense; you decreased the volume, and the pressure increased, which is exactly what Boyle’s law says.

Charles's law: Volume and temperature

Charles’s law (named after Jacques Charles, a 19th-century French chemist) has to do with the relationship between volume and temperature, keeping the pressure and amount of the gas constant. Ever leave a bunch of balloons in a hot car while running an errand? Did you notice that they expanded when you returned to the car?

Charles’s law says that the volume is directly proportional to the Kelvin temperature. Mathematically, the law looks like this:

This is a direct relationship: As the temperature increases, the volume increases, and vice versa. For example, if you placed a balloon in the freezer, the balloon would get smaller. Inside the freezer, the external pressure, or atmospheric pressure, is the same, but the gas particles inside the balloon aren’t moving as fast, so the volume shrinks to keep the pressure constant. If you heat the balloon, the balloon expands and the volume increases.

If the temperature of a gas with a certain volume (V₁) and Kelvin temperature (T₁) is changed to a new Kelvin temperature (T₂), the volume also changes (V₂):

The constant, b, is the same, so

(with the pressure and amount of gas held constant and temperature expressed in K)

If you have three of the quantities, you can calculate the fourth. For example, suppose you live in Alaska and are outside in the middle of winter, where the temperature is -23°C. You blow up a balloon so that it has a volume of 1.00 liter. You then take it inside your home, where the temperature is a toasty 27°C. What’s the new volume of the balloon?

First, convert your temperatures to Kelvin by adding 273 to the Celsius temperature:

Inside: -23°C + 273 = 250 K

Outside: 27°C + 273 = 300 K

Now you can solve for V₂, using the following setup:

Multiply both sides by T₂ so that V₂ is on one side of the equation by itself:

Then substitute the values to calculate the following answer:

It’s a reasonable answer, because Charles’s Law says that if you increase the Kelvin temperature, the volume increases.

Gay-Lussac's Law: Pressure and temperature

Gay-Lussac’s Law (named after the 19th-century French scientist Joseph-Louis Gay-Lussac) deals with the relationship between the pressure and temperature of a gas if its volume and amount are held constant. Imagine, for example, that you have a metal tank of gas. The tank has a certain volume, and the gas inside has a certain pressure. If you heat the tank, you increase the kinetic energy of the gas particles. So they’re now moving much faster, and they’re hitting the inside walls of the tank not only more often but also with more force. The pressure has increased.

Gay-Lussac’s Law says that the pressure is directly proportional to the Kelvin temperature. Mathematically, Gay-Lussac’s Law looks like this:

P = kT (or P/T = k at constant volume and amount)

Consider a gas at a certain Kelvin temperature and pressure (T₁ and P₁), with the conditions being changed to a new temperature and pressure (T₂ and P₂):

If you have a tank of gas at 800 torr pressure and a temperature of 250 Kelvin, and it’s heated to 400 Kelvin, what’s the new pressure? Starting with P₁/T₁ = P₂/T₂, multiply both sides by T₂ so you can solve for P₂:

Now substitute the values to calculate the following answer:

This is a reasonable answer because if you heat the tank, the pressure should increase.

The combined gas law: Pressure, Volume, and temp.

You can combine Boyle’s Law, Charles’s Law, and Gay-Lussac’s Law into one equation to handle situations in which two or even three gas properties change. Trust me, you don’t want me to show you exactly how it’s done, but the end result is called the combined gas law, and it looks like this:

P is the pressure of the gas (in atm, mm Hg, torr, and so on), V is the volume of the gas (in appropriate units), and T is the temperature (in Kelvin). The ₁ and ₂ stand for the initial and final conditions, respectively. The amount of gas is still held constant: No gas is added, and no gas escapes. There are six quantities involved in this combined gas law; knowing five allows you to calculate the sixth.

For example, suppose that a weather balloon with a volume of 25.0 liters at 1.00 atm pressure and a temperature of 27°C is allowed to rise to an altitude where the pressure is 0.500 atm and the temperature is -33°C. What’s the new volume of the balloon?

Before working this problem, do a little reasoning. The temperature is decreasing, so that should cause the volume to decrease (Charles’s Law). However, the pressure is also decreasing, which should cause the balloon to expand (Boyle’s Law). These two factors are competing, so at this point, you don’t know which will win out.

You’re looking for the new volume (V₂), so rearrange the combined gas law to obtain the following equation (by multiplying each side by T₂ and dividing each side by P₂, which puts V₂ by itself on one side):

Now identify your quantities:

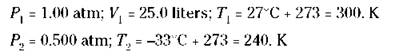
Now substitute the values to calculate the following answer:

Because the volume increased overall in this case, Boyle’s Law had a greater effect than Charles’s Law.

Avogadro's Law: The amount of gas

Amedeo Avogadro (the same Avogadro who gave us his famous number of particles per mole — see Chapter 9) determined, from his study of gases, that equal volumes of gases at the same temperature and pressure contain equal numbers of gas particles. So Avogadro’s law says that the volume of a gas is directly proportional to the number of moles of gas (number of gas particles) at a constant temperature and pressure. Mathematically, Avogadro’s law looks like this:

V = kn (at constant temperature and pressure)

In this equation, k is a constant and n is the number of moles of gas. If you have a number of moles of gas (n₁) at one volume (V₁), and the moles change due to a reaction (n₂), the volume also changes (V₂), giving you the equation

REMEMBER. A very useful consequence of Avogadro’s Law is that you can calculate the volume of a mole of gas at any temperature and pressure. An extremely useful form to know when calculating the volume of a mole of gas is that 1 mole of any gas at STP occupies 22.4 liters. STP in this case is not an oil or gas additive; it stands for standard temperature and pressure.

✓ Standard pressure: 1.00 atm (760 torr or mm Hg)

✓ Standard temperature: 273 K

This relationship between moles of gas and liters gives you a way to convert the gas from a mass to a volume. For example, suppose that you have 50.0 grams of oxygen gas (O₂) and you want to know its volume at STP. You can set up the problem like this (see Chapters 9 and 10 for the nuts and bolts of using moles in chemical equations):

You now know that the 50.0 grams of oxygen gas occupies a volume of 35.0 liters at STP.

If the gas isn’t at STP, you can use the combined gas law (from the preceding section) to find the volume at the new pressure and temperature — or you can use the ideal gas equation, which I show you next.

The ideal gas equation: Putting it alt together

If you take Boyle’s law, Charles’s law, Gay-Lussac’s law, and Avogadro’s law and throw them into a blender, turn the blender on high for a minute, and then pull them out, you get the ideal gas equation — a way of working in volume, temperature, pressure, and amount of a gas. The ideal gas equation has the following form:

The P represents pressure in atmospheres (atm), the V represents volume in liters (L), the n represents moles of gas, the T represents the temperature in Kelvin (K), and the R represents the ideal gas constant, which is 0.0821 liters atm/K-mol.

REMEMBER. Using the value of the ideal gas constant, the pressure must be expressed in atm, and the volume must be expressed in liters. You can calculate other ideal gas constants if you really want to use torr and milliliters, for example, but why bother? It’s easier to memorize one value for R and then remember to express the pressure and volume in the appropriate units. Naturally, you’ll always express the temperature in Kelvin when working any kind of gas law problem.

The ideal gas equation gives you an easy way to convert a gas from a mass to a volume if the gas is not at STP. For instance, what’s the volume of 50.0 grams of oxygen at 2.00 atm and 27.0°C? The first thing you have to do is convert the 50.0 grams of oxygen to moles using the molecular weight of O₂:

(50.0 grams) • (1 mol/32.0 grams) = 1.562 mol

Now take the ideal gas equation and rearrange it so you can solve for V:

Add your known quantities to calculate the following answer: