The Handy Chemistry Answer Book (2014)

ENERGY IS EVERYTHING

What is physical chemistry?

Physical chemistry is a branch of chemistry primarily concerned with developing a better understanding of the fundamental principles that govern chemical processes. It is an empirical science, meaning that it is based on experimental observations, though it is probably the most closely linked experimental branch of chemistry to developing new theories in chemistry. As the name implies, physical chemistry is intrinsically concerned with topics in physics that are also relevant to the study of chemistry.

What is energy?

In chemistry, energy serves as the “currency” for making or breaking chemical bonds and moving molecules (or matter) from one place to another.

What is potential energy?

Potential energy describes all of the nonkinetic energy associated with an object. This energy can be the energy stored in chemical bonds, in a compressed spring, or in a variety of other ways. Another example is gravitational potential energy, like that associated with a ball sitting at the top of a hill. Since there are many types of potential energy, there isn’t a single equation that describes them all. Since the value we assign to potential energy is always inherently described relative to some choice of a reference value, we can only actually measure changes in potential energy in a meaningful way. A closed system can exchange potential energy for kinetic and vice versa, but the total energy must always remain constant. This is stated in the First Law of Thermodynamics, which we’ll get to soon.

What is kinetic energy?

Kinetic energy is the type of energy associated with the movement of an object. Faster-moving objects have more kinetic energy, and the kinetic energy of an object is related to its mass, m, and velocity, v, by the equation:

E = ½mv²

This tells us that, for example, if we have two objects of equal mass and one is moving twice as fast as the other, the faster-moving object will have four times the energy of the slower object.

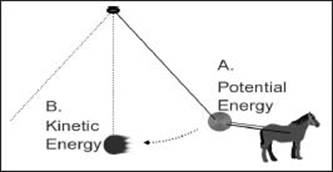
In this illustration, a horse pulls a pendulum into a position where it is about to be released to swing freely. Before it is released, the weight at the end of the pendulum has potential energy (A), and when the pendulum is in full swing, it has kinetic energy (B).

Can molecules have any arbitrary energy?

No, molecules actually have a discrete number of possible energy levels. Another way to say this is that their energies are quantized. To illustrate why this is so different from situations we’re used to in everyday life, consider what happens when you’re throwing a baseball. You could throw it at any speed between 0 meters per second (m/s) and however fast you are capable of throwing it. In molecules, though, only a discrete set of energies are possible. It’s as if you could throw the baseball either 2 m/s or 40 m/s, but not 20 m/s or any other speed in between. There aren’t many situations we encounter in everyday life in which the possible energies associated with objects come in a discrete set of values.

What types of energy levels exist in molecules?

There are three main types of energy levels that physical chemists are concerned with. These are electronic, vibrational, and rotational energies. Changes in electronic energy levels occur when an electron undergoes a transition from one molecular orbital to another. Vibrational energy levels are associated with vibrations of chemical bonds in the molecule, and rotational energy levels involve the molecule rotating in space. As you could probably guess, atoms don’t have vibrational energy levels since there aren’t chemical bonds present in single atoms. Physical chemists can often learn about the structure and reactivity of molecules by studying the transitions between these energy levels.

What is quantum mechanics?

Quantum mechanics is a branch of physics that is needed to provide an accurate description of objects with very small mass, such as electrons. It does so using an approach that describes matter as being both similar to a particle and similar to a wave. The description of a particle in quantum mechanics is contained in something called a wave function, which can be related to the probability of an object being in any of its possible states.

One interesting and counterintuitive thing we learn from quantum mechanics is that, for particles with very small mass, the position, velocity, and other quantities defining the state of the particle cannot all be precisely specified at the same time. The wavelike description offered by quantum mechanics is needed to explain why molecules have discrete energy levels, along with many other experimental observations from physical chemistry that are inconsistent with classical mechanics.

What is work?

Work is a name used in physics for processes that transfer energy between objects by the application of a force over a distance. Take throwing a baseball, for example. As your arm moves, your hand applies a force in the direction the baseball is moving. During the time the ball is in your hand and moving forward, you are doing work on the ball. The total amount of work done can be calculated as the product of the force you apply times the distance over which you applied force. Once it leaves your hand, you’re no longer applying a force, so you aren’t doing work on it anymore.

What is heat?

Heat is responsible for all types of energy transfer other than those that fall under the definition of work. One easy example to think about is ice cream melting on a hot day. Because the ice cream is at a lower temperature than its surroundings, heat flows from the surroundings to the ice cream, causing its temperature to increase, and eventually it melts. There are lots of other examples of heat flow too; it’s a pretty big category since it covers all types of energy transfer that aren’t defined as work.

What is the zeroth law of thermodynamics?

The zeroth law of thermodynamics states that any two systems, call them A and B, that are each in thermal equilibrium with a third system, call it C, must be in thermal equilibrium with each other. Thermal equilibrium implies that the systems must have the same temperature, and therefore systems A and B must have the same temperature. This might seem totally obvious, but it is what puts our use of thermometers to compare the temperatures of different objects on a sound footing. If object C is our thermometer, we can use it to compare the temperatures of other objects.

What is the first law of thermodynamics?

The first law of thermodynamics is a statement of the conservation of energy, which tells us that energy can be transferred from one form to another but never created or destroyed. It tells us how energy is related to work and heat, and it is typically stated through the equation:

δE = δQ – δW

This equation tells us that the differential change in energy (δE) is equal to the heat (δQ) that flows into the system minus the work (δW) the system does on its surroundings.

What is entropy?

Entropy is a measure of the total number of microstates in a system. There have been two widely used definitions of entropy, which were suggested by Ludwig Boltzmann and J. Willard Gibbs. We’ll just look at the one specified by Boltzmann, since it’s a little more straightforward to understand. The equation for Boltzmann’s definition of entropy is:

S = k_b ln( )

In this equation, k_b is Boltzmann’s constant, and is the number of microstates accessible to a system.

To get an idea of how entropy works, consider the example of rolling one or more six-sided die. On the first roll, there are six possible outcomes, so the entropy associated with rolling one die is k_bln(6). If we roll two dice, there are 6² = 36 possible outcomes, and the associated entropy is k_b ln(36). For three, it’s 6³ = 216 possible outcomes, and the associated entropy is k_bln(216). As you can see, the number of outcomes for statistically independent events grows very rapidly (exponentially) with the size of our system, which is also true for molecules. By taking the logarithm of the number of outcomes, we make the entropy scale linearly with system size. While the number of possible outcomes/configurations grows exponentially with system size, the entropy grows linearly, which means that if we double the system size we double the entropy. This property makes entropy fall into a category of variables known as extensive variables, which just means that they scale with the size of a system in this simple way.

What is the second law of thermodynamics?

There are several different statements of the second law of thermodynamics, but they are all centered on the idea of identifying what things can happen spontaneously in nature.

One formulation of the second law states that, for a closed system, the entropy of the system can only increase or remain the same. In plain language, this says that nature favors having more accessible configurations or arrangements. It’s why, for example, a drop of ink in water tends to spread out to fill its accessible volume but won’t spontaneously reform a drop of ink.

Another statement of the second law says that heat cannot spontaneously flow from a colder body to a warmer body. Work would have to be done for this to happen, which would imply the process was not spontaneous.

What is the third law of thermodynamics?

The most common statement of the third law of thermodynamics is that the entropy of a perfectly crystalline system approaches zero as the temperature of the system approaches zero. (Recall from “Macroscopic Properties: The World We See” that a perfect crystal is a regularly ordered lattice of atoms that exist in a repeating pattern in three dimensions with no defects or irregularities in the lattice.) This is equivalent to saying that a perfectly crystalline system has only one accessible state as the temperature approaches zero. In truth, this isn’t always strictly true since there can be multiple low-energy states that all have the similar energy, but let’s ignore this for now.

What effects cause deviations from the ideal gas law?

Deviations from the ideal gas law occur due to intermolecular forces between the gas particles as well as the fact that gas particles do actually occupy volume. There is a modified version of the ideal gas law (see “Atoms and Molecules”), called the van der Waals equation of state, that uses constants specific to each molecule or atom to adjust for these factors. Deviations from ideal gas law behavior become more important at relatively high pressures and/or low temperatures.

What is the average kinetic energy of a molecule?

The average kinetic energy of a molecule is closely related to the temperature of its environment, and this determines how fast the molecule is moving. On average, the speed of any molecule is close to 300 m/s, which is equivalent to covering the distance of a few football fields every second! The other important thing to realize, though, is that collisions with other molecules are constantly causing changes in direction, which slows the overall distance in a given direction that a molecule travels.

What is an ideal solution?

An ideal solution describes a solution of dilute solute particles that do not interact with one another. It is very similar to an ideal gas, except that instead of empty space occupying the space between the gas particles, a weakly interacting solvent occupies the space between solute particles.

What is osmosis?

Osmosis is the movement of solvent molecules in a solution to establish an equal concentration of solute throughout the solution. Solvent molecules move from areas of low-solute concentration to areas of high-solute concentration, which tends to remove any gradient in solute concentration.

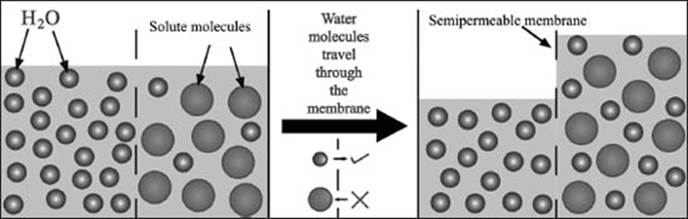
In osmosis, solvent molecules move from areas of low solute concentration to areas of high solute concentration through a permeable membrane to equalize the solute concentration on either side.

What is an isothermal process?

An isothermal process is a process in which the temperature remains constant throughout the process.

What is an isobaric process?

An isobaric process is a process that is carried out at a constant pressure.

What is an adiabatic process?

An adiabatic process is a process in which no heat is exchanged with the surroundings.

What is an isochoric process?

An isochoric process is a process that takes place at a constant volume.