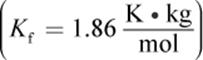MCAT General Chemistry Review
Chapter 9: Solutions
9.4 Colligative Properties
The colligative properties are physical properties of solutions that are dependent on the concentration of dissolved particles but not on the chemical identity of the dissolved particles. These properties—vapor pressure depression, boiling point elevation, freezing point depression, and osmotic pressure—are usually associated with dilute solutions.
RAOULT’S LAW
Raoult’s Law accounts for vapor pressure depression caused by solutes in solution. As solute is added to a solvent, the vapor pressure of the solvent decreases proportionately. For example, consider compound A in Figure 9.9. Compound A in its pure form (mole fraction = 1.0) has a particular vapor pressure, indicated by PA° . At the same temperature, compound B has a lower vapor pressure, indicated by PB° . Note that, as the concentration of B increases, the vapor pressure of A decreases. Indeed, as more solute is dissolved into solvent (as more B is dissolved into A), the vapor pressure of the solvent decreases.
Figure 9.9. Raoult’s Law As more of solute B is dissolved in solvent A, the vapor pressure of solvent A decreases.
On a molecular level, the presence of the solute molecules can block the evaporation of solvent molecules but not their condensation. This reduces the vapor pressure of the solution compared to the pure solvent, as seen in Figure 9.10.
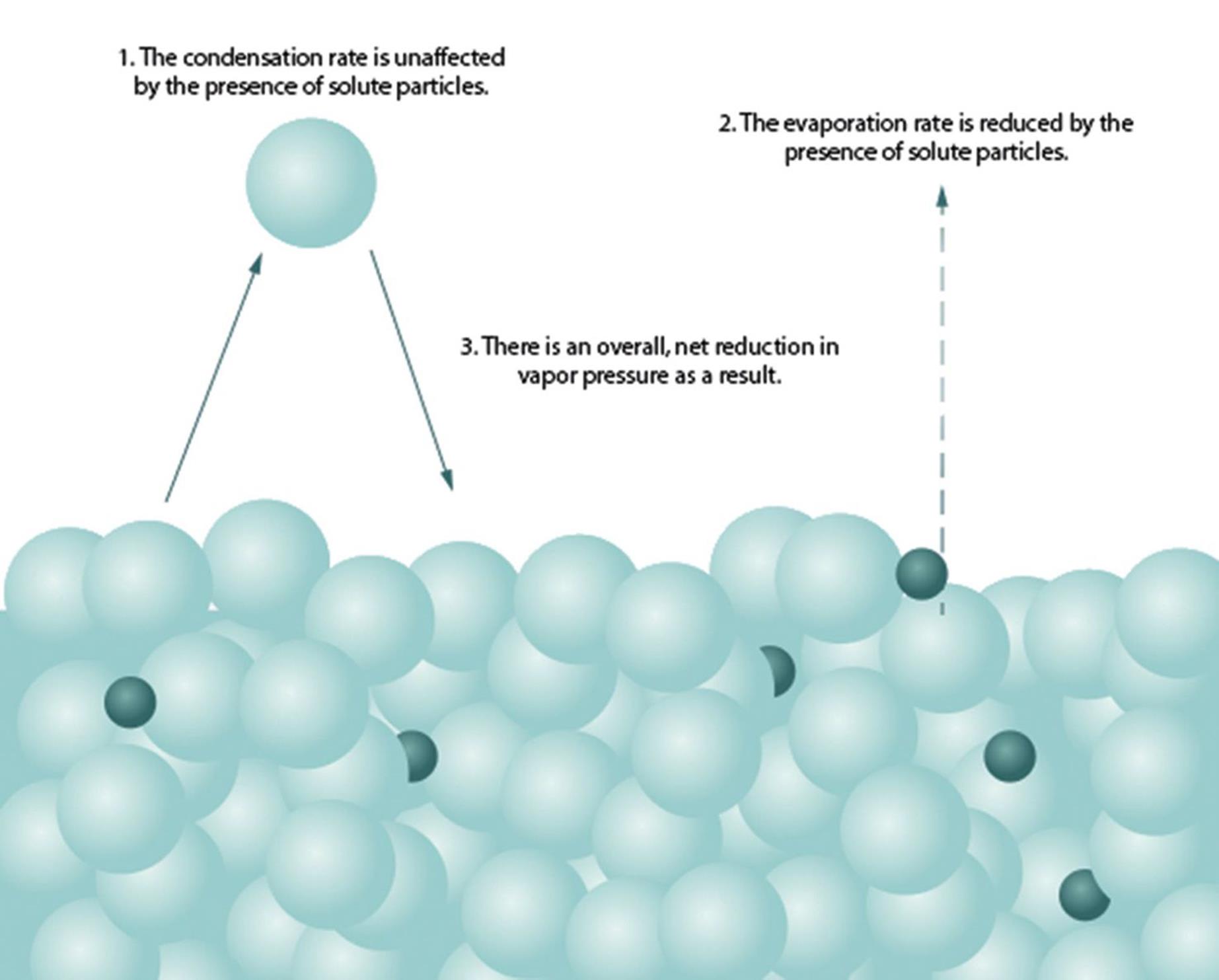Figure 9.10. Molecular Basis of Raoult’s Law
Raoult’s law is expressed mathematically as
PA = XAPA°
Equation 9.8
where PA is the vapor pressure of solvent A when solutes are present, XA is the mole fraction of the solvent A in the solution, and PA° is the vapor pressure of solvent A in its pure state.
KEY CONCEPT
Vapor pressure depression goes hand in hand with boiling point elevation. The lowering of a solution’s vapor pressure would mean that a higher temperature is required to match atmospheric pressure, thereby raising the boiling point.
Raoult’s law holds only when the attraction between the molecules of the different components of the mixture is equal to the attraction between the molecules of any one component in its pure state. When this condition does not hold, the relationship between mole fraction and vapor pressure will deviate from Raoult’s law. Solutions that obey Raoult’s law are called ideal solutions.
Example:
What is the change in vapor pressure when 180 grams of glucose (C6H12O6) are added to 0.18 L of water at 100°C?
Solution:
The density of water at 100°C is close to 
and the vapor pressure of water at the same temperature is 1 atm because this is the boiling point of water.
In order to find the mole fraction of the solvent, first find the molar mass of the solute (glucose) and solvent (water). 180 g glucose represents 1 mole of glucose. 0.18 L of water has a mass around 180 g, which represents 10 moles of water. The mole fraction of water is therefore 
To find the vapor pressure change, we want to find the difference in the old pressure and the new pressure. The new pressure can be calculated from Raoult’s law:
PA = XAPA° = (0.91)(1 atm) = 0.91 atm.
The change in vapor pressure is therefore 1 atm – 0.91 atm = 0.09 atm.
Example:
What is the vapor pressure at room temperature of a mixture containing 58 g butane (C4H10) and 172 g hexane (C6H14)? (Note: the vapor pressures of pure butane and pure hexane are 172 kPa and 17.6 kPa, respectively, at 25°C.)
Solution:
First, determine the number of moles of each substance. 58 g butane represents 1 mole of butane. 172 g hexane represents 2 moles of hexane. Then, determine the mole fractions of each component of the mixture.
Then, calculate the vapor pressure of each component.
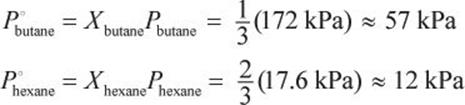
The total vapor pressure is just the sum of these two vapor pressures. Thus, the total vapor pressure is 57 + 12 = 69 kPa (actual = 69.1 kPa).
BOILING POINT ELEVATION
When a nonvolatile solute is dissolved into a solvent to create a solution, the boiling point of the solution will be greater than that of the pure solvent. The boiling point is the temperature at which the vapor pressure of the liquid equals the ambient (incident) pressure. We’ve just seen that adding solute to a solvent results in a decrease in the vapor pressure of the solvent in the solution. If the vapor pressure of a solution is lower than that of the pure solvent, then more energy (and consequently a higher temperature) will be required before its vapor pressure equals the ambient pressure. The extent to which the boiling point of a solution is raised relative to that of the pure solvent is given by the formula
ΔTb = iKbm
Equation 9.9
where ΔTb is the increase in boiling point, i is the van ’t Hoff factor, Kb is a proportionality constant characteristic of a particular solvent (which will be provided on Test Day), and m is the molality of the solution. The van ’t Hoff factor corresponds to the number of particles into which a compound dissociates in solution. For example, i = 2 for NaCl because each formula unit of sodium chloride dissociates into two particles—a sodium ion and a chloride ion—when it dissolves. Covalent molecules such as glucose do not readily dissociate in water and thus have i values of 1.
MCAT EXPERTISE
The boiling point elevation formula calculates the amount that the normal boiling point is raised. The value calculated is not the boiling point itself.
Example:
400 g AlCl3 is dissolved in 1.5 L of water at room temperature
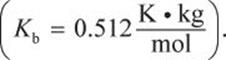
How much does the boiling point increase after adding the aluminum chloride?
Solution:
Water at room temperature has a density of 
Therefore, 1.5 L is the same as 1.5 kg. The van ’t Hoff factor for aluminum chloride is 4 because it breaks down to form 1 aluminum cation and 3 chloride anions. To determine the molality, we will also need to know how many moles 400 g AlCl3 represents.
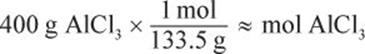
The molality is therefore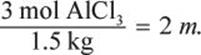 
Then, plug into the boiling point elevation equation.
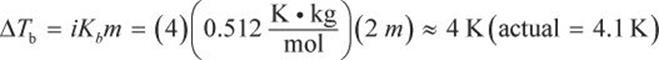
FREEZING POINT DEPRESSION
The presence of solute particles in a solution interferes with the formation of the lattice arrangement of solvent molecules associated with the solid state. Thus, a greater amount of energy must be removed from the solution (resulting in a lower temperature) in order for the solution to solidify. For example, pure water freezes at 0°C, but for every mole of solute dissolved in 1 kg of water, the freezing point is lowered by 1.86°C. Therefore, the Kf for water is 
As is the case for Kb, the values for Kf are unique to each solvent and will be provided on Test Day. The formula for calculating the freezing point depression for a solution is
ΔTf = iKfm
Equation 9.10
where ΔTf is the freezing point depression, i is the van ’t Hoff factor, Kf is the proportionality constant characteristic of a particular solvent, and m is the molality of the solution. Freezing point depression is a colligative property and depends only on the concentration of particles, not on their identity.
Example:
400 g of AlCl3 is dissolved in 1.5 L of water at room temperature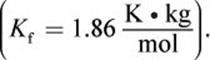 
What is the new freezing point of this solution?
Solution:
Using the same variables for i and m from the previous example,
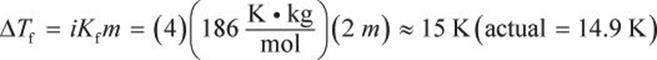
The normal freezing point of water is 273 K. The freezing point is going to be depressed (or decreased) by 15 K. The new freezing point is therefore 273 – 15 = 258 K = –15°C.
MCAT EXPERTISE
As with boiling point elevation, there is a distinction between the calculated value and a final answer. The freezing point depression calculates the amount that the normal freezing point is lowered. As always, read the question to determine if it is asking for the change in temperature (ΔT) or the new (altered) boiling or freezing point.
This effect is the explanation for why we salt icy roads in the winter. Salt mixes with the snow and ice and initially dissolves into the small amount of liquid water that is in equilibrium with the solid phase (the snow and ice). The solute in solution causes a disturbance to the equilibrium such that the rate of melting is unchanged (because the salt can’t interact with the solid water that is stabilized in a rigid lattice arrangement), but the rate of freezing is decreased (the solute displaces some of the water molecules from the solid–liquid interface and prevents liquid water from entering into the solid phase).
This imbalance causes more ice to melt than water to freeze. Melting is an endothermic process, so heat is initially absorbed from the liquid solution, causing the solution temperature to fall below the ambient temperature. Now, there is a temperature gradient, and heat flows from the warmer air to the cooler aqueous solution; this additional heat facilitates more melting—even though the temperature of the solution is actually colder than it was before the solute was added! The more the ice melts into liquid water, the more the solute is dispersed through the liquid. The resulting salt solution, by virtue of the presence of the solute particles, has a lower freezing point than the pure water and remains in the liquid state even at temperatures that would normally cause pure water to freeze.
OSMOTIC PRESSURE
Osmotic pressure is covered primarily in Chapter 8 of MCAT Biochemistry Review, but a brief recap is provided here. Osmotic pressure refers to a “sucking” pressure generated by solutions in which water is drawn into a solution. Formally, the osmotic pressure is the amount of pressure that must be applied to counteract this attraction of water molecules for the solution. The equation for osmotic pressure is
∏ = iMRT
Equation 9.11
where ∏ is the osmotic pressure, i is the van ’t Hoff factor, M is the molarity of the solution, R is the ideal gas constant, and T is the temperature.
Water moves in the direction of higher solute concentration. For instance, pure water (no solute concentration) will traverse a semipermeable membrane to a solution containing solute particles (such as NaCl) and increase the level of the water as a result, as shown in Figure 9.11.
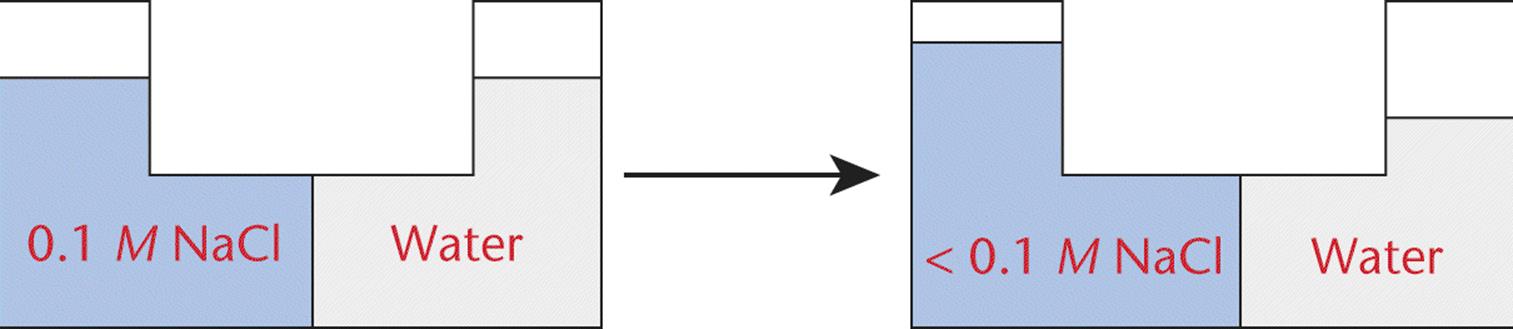Figure 9.11. Change in Water Level Due to Osmotic Pressure
MCAT Concept Check 9.4:
Before you move on, assess your understanding of the material with these questions.
1. What is a colligative property?
2. How are molality and molarity related for water? How are they related for other solvents?
· Water:
· Other solvents:
3. Determine the vapor pressure of a solution containing 190 g MgCl2 in 720 g water at room temperature: (Note: The vapor pressure of pure water at 25°C is 3.2 kPa.)
4. Determine the new boiling point of a solution containing 190 g MgCl2 in 1800 g water at room temperature:
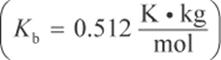
5. Determine the freezing point depression of a solution containing 58.5 g of NaCl in 2160 g of water at room temperature:
