MCAT General Chemistry Review
Chapter 10: Acids and Bases
10.2 Properties
Acids and bases are usually characterized according to their relative tendencies to either donate or accept hydrogen ions. Furthermore, aqueous acid and base solutions can be characterized according to their concentrations of hydrogen and hydroxide ions.
AUTOIONIZATION OF WATER AND HYDROGEN ION EQUILIBRIA
Because many acid–base reactions take place in water—especially on the MCAT—it is very important to understand the behavior of acidic and basic compounds in water. Only then can one fully appreciate the meaning and significance of such terms as strong acid, weak base, or measurements of pH and pOH.
The Acid–Base Behavior of Water
As described above, water is an amphoteric species: in the presence of a base it reacts as an acid, and in the presence of an acid, it reacts as a base. As an amphoteric compound, water can react with itself in a process called autoionization, seen previously in Figure 10.1. The autoionization of water is represented by the equation:
H2O (l) + H2O (l) ⇌ H3O+ (aq) + OH− (aq)
One water molecule donates a hydrogen ion to another water molecule to produce the hydronium ion (H3O+) and the hydroxide ion (OH−). Many general chemistry courses depict the hydrogen ion simply as H+, rather than as H3O+.
This is acceptable for representing the chemistry, but it is important to remember that the proton is never isolated in the solution; it is always attached to water or some other species that has the ability to accept it. Autoionization of water is a reversible reaction; therefore, the expression above is in equilibrium. For pure water at 298 K, the water dissociation constant, Kw, has been experimentally determined:
Kw = [H3O+][OH−] = 10−14 at 25°C (298 K)
Equation 10.1
Each mole of water that autoionizes produces one mole each of hydrogen (or hydronium) ions and hydroxide ions, so the concentrations of the hydrogen ions and hydroxide ions are always equal in pure water at equilibrium. Thus, the concentration of each of the ions in pure water at equilibrium at 298 K is 10−7 M.
However, the concentrations of the two ions will not always be equal. In fact, they will only be equal when the solution is neutral. Nevertheless, the product of their respective concentrations will always equal 10−14 when the temperature of the solution is 298 K. For example, if a species donates hydrogen ions to pure water, the hydrogen ion concentration will increase, causing the system to shift toward the reactants in the autoionization process. The result is a decrease in the hydroxide ion concentration and a return to the equilibrium state. This is Le Châtelier’s principle in action: the addition of product to a system at equilibrium causes the system to shift away from the products and toward the reactants. The shift away from the products necessarily decreases the hydroxide ion concentration such that the product of the concentrations of the dissolved ions equals Kw. The addition of a species that accepts hydrogen ions results in a decrease in the hydrogen ion concentration and causes the system to shift toward the products, thereby replacing hydrogen ions. This shift necessarily increases the hydroxide ion concentration and returns the system to equilibrium.
Before we introduce the scales used in measuring concentrations of hydrogen ions and hydroxide ions in different acid–base solutions, it is worthwhile to emphasize an important thermodynamic principle regarding the water dissociation constant (Kw) expression. Kw is an equilibrium constant; unless the temperature of the water is changed, the value for Kw cannot be changed. Thus, the product of the concentrations of the hydrogen ions and the hydroxide ions in an aqueous solution at 298 K must always equal 10−14. However, at different temperatures, the value for Kwchanges. At temperatures above 298 K, Kw will increase; this is a direct result of the endothermic nature of the autoionization reaction.
MCAT EXPERTISE
The MCAT loves to test this concept: the value of Kw, like any other equilibrium constant, is dependent only on temperature. Therefore, isolated changes in concentration, pressure, or volume will not affect Kw.
pH and pOH Scales
The concentrations of hydrogen ions and hydroxide ions in aqueous solutions can vary significantly, making the range of measurements on a linear scale unmanageable. The concentration scales for acidic and basic solutions are condensed into something more manageable through expression in logarithmic terms. These logarithmic scales are the pH and the pOH scales for the concentrations of hydrogen and hydroxide ions, respectively.
BRIDGE
Logarithmic scales are used to condense very large absolute differences into small scale differences. Remember that sound level (dB) also uses a logarithmic scale, as discussed in Chapter 7 of MCAT Physics and Math Review.
Using a logarithmic scale is not only mathematically convenient, but also useful for calculations. For instance, the reactivity of an acidic solution is not a function of hydrogen ion concentration but instead of the logarithm of the hydrogen ion concentration. pH and pOH are prototypical examples of p scales. A p scale is defined as the negative logarithm of the number of items.
The pH and pOH of a solution are given by
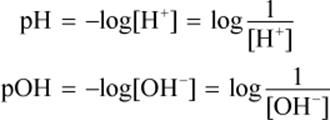
Equation 10.2
For pure water at equilibrium and 298 K, the concentration of hydrogen ions equals the concentration of hydroxide ions (10−7 M). Therefore, pure water at 298 K has a pH of 7 and a pOH of 7 (−log 10−7 = 7). If we take the negative logarithm of the entire water dissociation constant expression ([H3O+][OH−] = 10−14), we find that
pH + pOH = 14
Equation 10.3
for all aqueous solutions at 298 K. As pH increases, pOH decreases by the same amount. This relationship can be seen in Figure 10.5 below.
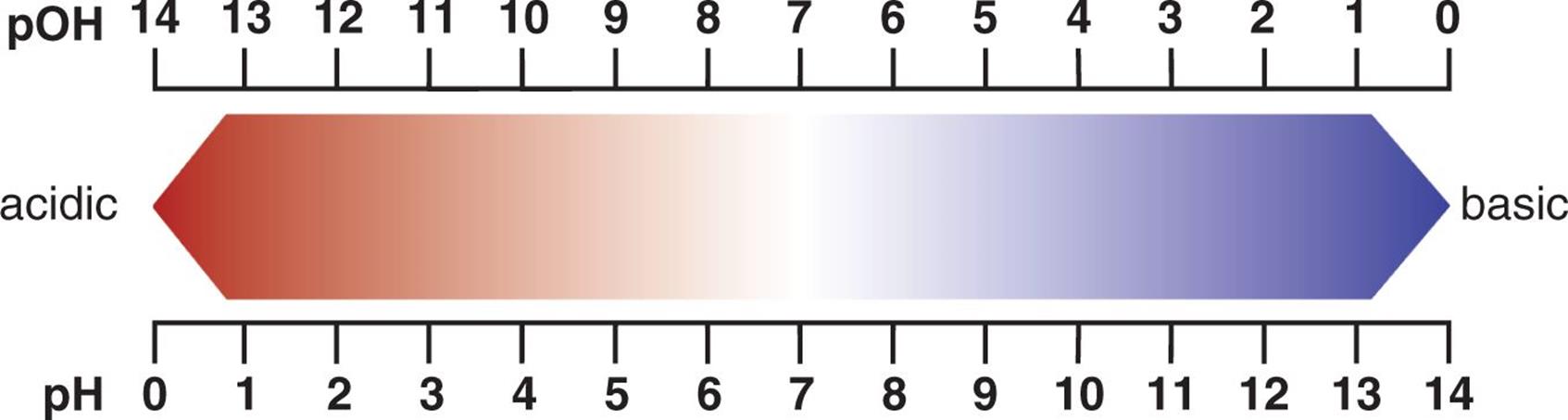 Figure 10.5. pH and pOH Scales pH + pOH = 14 for aqueous solutions at 298 K.
Figure 10.5. pH and pOH Scales pH + pOH = 14 for aqueous solutions at 298 K.
MCAT EXPERTISE
The Kw (like all equilibrium constants) will change if the temperature changes and, in turn, will change the significance of the pH scale. Be careful and read the system conditions given on the MCAT: pH = 7 = neutral is only valid at 25°C.
BRIDGE
In general, math using logarithms frequently appears on the MCAT; make sure to review how these mathematical concepts work in Chapter 10 of MCAT Physics and Math Review. Specifically, the equation pH + pOH = 14 comes from the fact that the log of a product is equal to the sum of logs; that is, log (xy) = log x + log y.
For an aqueous solution at 298 K, a pH less than 7 (or pOH greater than 7) indicates a relative excess of hydrogen ions, and the solution is acidic; a pH greater than 7 (or pOH less than 7) indicates a relative excess of hydroxide ions, and the solution is basic. A pH (and pOH) equal to 7 indicates equal concentrations of hydrogen and hydroxide ions, resulting in a neutral solution.
Estimating Scale Values
An essential skill to hone for Test Day is the ability to quickly convert pH, pOH, pKa, and pKb values into nonlogarithmic form and vice-versa.
When the original value is a power of ten, the operation is relatively straightforward: changing the sign on the exponent gives the corresponding p scale value directly. For example, if [H+] = 0.001 or 10−3, then the pH = 3 and pOH = 11. Or, if Kb = 1.0 × 10−12, then pKb = 12.
More difficulty arises when the value is not an exact power of ten. Rest assured that the MCAT is not a math test and is not interested in determining your ability to perform complex logarithmic calculations; an exact logarithmic calculation of a number that is not an integer power of ten is unnecessary on the MCAT. The testmakers are interested, however, in testing the ability to apply mathematical concepts appropriately in solving certain problems.
One can obtain a relatively close approximation of a p scale value using the following shortcut: if the nonlogarithmic value is written in proper scientific notation, it will be in the form n × 10−m, where n is a number between 1 and 10. Taking the negative logarithm and simplifying, the p value will be:
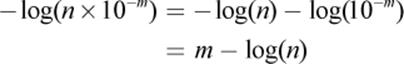
Because n is a number between 1 and 10, its logarithm will be a decimal between 0 and 1 (log 1 = 0 and log 10 = 1). The closer n is to 1, the closer log n will be to 0; the closer n is to 10, the closer log n will be to 1. As a reasonable approximation, one can say that
p value ≈ m − 0.n
Equation 10.4
where 0.n represents sliding the decimal point of n one position to the left (dividing n by ten).
Example:
If the Ka of an acid is 1.8 × 10−5, then what is its pKa?
Solution:
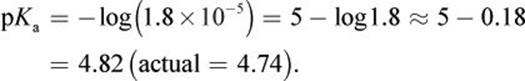
MCAT EXPERTISE
Learning how to estimate when using logarithms is an important skill that can save a lot of time on Test Day.
STRONG ACIDS AND BASES
Strong acids and bases completely dissociate into their component ions in aqueous solutions. For example, when sodium hydroxide is added to water, the ionic compound dissociates according to the net ionic equation:
NaOH (s) → Na+ (aq) + OH− (aq)
Hence, in a 1 M NaOH solution, complete dissociation yields 1 M Na+ and 1 M OH−. The pH and pOH for this solution can be calculated as follows:
pH = 14 − pOH = 14 − (−log[OH−]) = 14 + log (1 M) = 14 + 0 = 14
MCAT EXPERTISE
Acid–base reactions that consist of a single-headed arrow generally indicate strong acids or bases (complete dissociation with no reversibility).
Virtually no undissociated strong acid or base, such as NaOH, will remain in solution. This is why the dissociation of strong acids and bases is said to go to completion. In the NaOH example above, we assume that the concentration of OH− from the autoionization of water is negligible due to addition of a strong base. The contribution of OH− and H+ ions from the autoionization of water is negligible if the concentration of the acid or base is significantly greater than 10−7 M. On the other hand, if the concentration of acid or base is close to 10−7 M, then the contribution from the autoionization of water is important.
Example:
Calculate the pH of a 1 × 10−8 M solution of HCl.
Solution:
At first, one may calculate the pH as −log [H+] = −log 10−8 M = 8. However, this answer is not feasible: a pH of 8 cannot describe an acidic solution at 298 K because the presence of the acid will increase the hydrogen ion concentration to above 10−7 M, resulting in an acidic pH below 7.
Recognize that the acid concentration in this question is actually ten times less than the equilibrium concentration of hydrogen ions in pure water generated by the autoionization of water. Consequently, the hydrogen ion concentration from the water itself is significant and cannot be ignored. This can be represented in the equilibrium expression in which x represents the concentration of H3O+ and OH− resulting from the autoionization of water:
Kw = [H3O+][OH−] = [x + 10−8][x] = 10−14
Solving for x (which would require a quadratic equation—math that is beyond the scope of the MCAT) gives x = 9.5 × 10−8 M. The total concentration of hydrogen ions is [H+]total = (9.5 × 10−8) + (1.0 × 10−8) = 1.05 × 10−7 M. Notice that this is extremely close to the concentration of H+ in pure water. The pH of this acidic solution can now be calculated as pH = −log(1.05 × 10−7) ≈ 7 (actual = 6.98). This pH is slightly lower than 7, as expected for a very dilute acidic solution. The point of all of this is: stay alert and keep thinking critically, no matter how familiar the problem setups might seem to you!
Strong acids commonly encountered on the MCAT include HCl (hydrochloric acid), HBr (hydrobromic acid), HI (hydroiodic acid), H2SO4 (sulfuric acid), HNO3 (nitric acid), and HClO4 (perchloric acid). Strong bases commonly encountered include NaOH (sodium hydroxide), KOH (potassium hydroxide), and other soluble hydroxides of Group IA metals. Calculation of the pH and pOH of strong acids and bases assumes complete dissociation of the acid or base in solution.
Example:
What is the pH of a solution with [HClO4] = 10 M?
Solution:
Because perchloric acid is a strong acid, it will fully dissociate in solution. Therefore, [H+] = 10 M (note that the contribution from the autoionization of water is negligible). pH = −log [H+] = −log 10 M = −1. This question points out that the pH scale does not “end” at 0 and 14. There can be negative pH values and pH values greater than 14—but this implies a very high concentration of a strong acid or base.
WEAK ACIDS AND BASES
Before going any further in our discussion of acids and bases as strong or weak, verify that you are making the distinction between the chemical behavior of an acid or base with respect to its tendency to dissociate (that is, strong bases completely dissociate in aqueous solutions) and the concentrations of acid and base solutions. Although we may casually describe a solution’s concentration as strong or weak, it is preferable to use the terms concentrated and dilute, respectively, because they are unambiguously associated with concentrations, rather than chemical behavior.
Continuing our focus on the chemical behavior of acids and bases, we will now consider those acids and bases that only partially dissociate in aqueous solutions. These are called weak acids and bases. A weak monoprotic acid, HA, will dissociate partially in water to achieve an equilibrium state:
HA (aq) + H2O (l) ⇌ H3O+ (aq) + A− (aq)
Because the system exists in an equilibrium state, we can write the dissociation equation to determine the acid dissociation constant (Ka) as
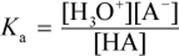
Equation 10.5
The smaller the Ka, the weaker the acid, and consequently, the less it will dissociate. Note that water, as a pure liquid, is not incorporated into the equilibrium expression.
A weak monovalent Arrhenius base, BOH, undergoes dissociation to yield B+ and OH− in solution:
BOH (aq) ⇌ B+ (aq) + OH− (aq)
The base dissociation constant (Kb) can be calculated as
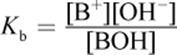
Equation 10.6
The smaller the Kb, the weaker the base, and consequently, the less it will dissociate. As with the acid dissociation expression, water is not included because it is a pure liquid.
Generally speaking, we can characterize a species as a weak acid if its Ka is less than 1.0 and as a weak base if its Kb is less than 1.0. On the MCAT, molecular (nonionic) weak bases are almost exclusively amines.
CONJUGATE ACID–BASE PAIRS
Because the Brønsted–Lowry definition of an acid–base reaction is one in which a hydrogen ion (proton) is transferred from an acid to a base, the two always occur in pairs called conjugates. A conjugate acid is the acid formed when a base gains a proton, and a conjugate base is the base formed when an acid loses a proton. For example,
HCO3− (aq) + H2O (l) ⇌ CO32− (aq) + H3O+ (aq)
CO32− is the conjugate base of HCO3−, a weak acid, and H3O+ is the conjugate acid of H2O, a weak base. To find the Ka, we consider the equilibrium concentrations of the dissolved species:
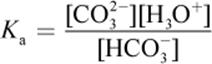
The reaction between bicarbonate and water is reversible. The reverse reaction would be:
CO32− (aq) + H2O (l) ⇌ HCO3− (aq) + OH− (aq)
We can write the Kb for CO32− as:
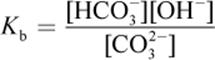
If one adds the previous two reversible reactions, the net reaction is simply the dissociation of water:
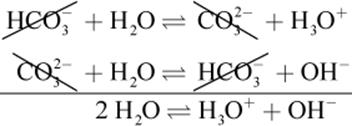
Because the net reaction is the autoionization of water, the equilibrium constant for the reaction is Kw = [H3O+][OH−] = 10−14, which is the product of Ka and Kb. Remember: the product of the concentrations of the hydrogen ion and the hydroxide ion must always equal 10−14 for acidic or basic aqueous solutions. Because water is an amphoteric species (both a weak acid and a weak base), all acid–base reactivity in water ultimately reduces to the acid–base behavior of water, and all acidic or basic aqueous solutions are governed by the dissociation constant for water. Thus, if the dissociation constant for one species or its conjugate is known, then the dissociation constant for the other can be determined using the following equations:

Equation 10.7
As is evident from these equations, Ka and Kb are inversely related. In other words, if Ka is large, then Kb is small, and vice-versa. By this logic, a strong acid (Ka approaching ∞) will produce a very weak conjugate base (for example, HCl is a strong acid and Cl− is a very weak base), and a strong base will produce a very weak conjugate acid (for example, NaOH is a strong base and H2O is a very weak acid). The conjugate of a strong acid or base is sometimes termed inert because it is almost completely unreactive.
KEY CONCEPT
Be aware of the relationship between conjugate acids and bases because you will need to recognize these entities on the MCAT. Removing a proton from a molecule produces the conjugate base, and adding a proton produces the conjugate acid.
On the other hand, weak acids and bases tend to have conjugates that are also weak. As seen above, CO32− is a weak base; its conjugate acid, HCO3− is a weak acid. As it turns out, for this specific example, the reaction of CO32− with water to produce CO32− and OH− occurs to a greater extent—is more thermodynamically favorable—than the reaction of HCO3− and water to produce CO32− and H3O+. This fact makes this equilibrium ideal for buffering solutions as part of the bicarbonate buffer system, discussed in Chapter 6 of MCAT Biology Review.
BRIDGE
This thermodynamic preference for the bicarbonate ion intermediate is the major reason why the bicarbonate buffer system in the body is ideal for maintaining a stable pH. The homeostatic mechanisms involved are discussed in Chapter 6 of MCAT Biology Review.
One important theme for acid strength is the effect of induction. Electronegative elements positioned near an acidic proton increase acid strength by pulling electron density out of the bond holding the acidic proton. This weakens proton bonding and facilitates dissociation. Thus, acids that have electronegative elements nearer to acidic hydrogens are stronger than those that do not, as shown in Figure 10.6.
 Figure 10.6. Inductive Effects from Electronegative Elements Increase Acidity
Figure 10.6. Inductive Effects from Electronegative Elements Increase Acidity
APPLICATIONS OF Ka AND Kb
The most common use of acid and base dissociation constants is to determine the concentration of one of the species in solution at equilibrium. On Test Day, you may be asked to calculate the concentration of the hydrogen ion (or pH), the concentration of the hydroxide ion (or pOH), or the concentration of either the original acid or base.
Example:
Calculate the concentration of H3O+ in a 2.0 M aqueous solution of acetic acid, CH3COOH. (Note: Ka = 1.8 × 10−5)
Solution:
First, write the equilibrium reaction:
CH3COOH (aq) + H2O (l) ⇌ H3O+ (aq) + CH3COO− (aq)
Next, write the expression for the acid dissociation constant:
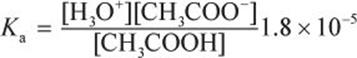
Then, recognize that acetic acid is a weak acid, so the concentration of CH3COOH at equilibrium is equal to its initial concentration, 2.0 M, minus the amount dissociated, x. Likewise, [H3O+] = [CH3COO−] = x because each molecule of CH3COOH dissociates into one H+ ion and one CH3COO− ion. Note that the contribution of H3O+ from water is negligible. Thus, the equation can be rewritten as follows:
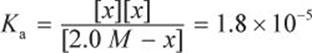
Remember that the value of x is generally very small. Therefore, we can approximate that 2.0 M − x ≈ 2.0 M. This is further supported because acetic acid is a weak acid and only slightly dissociates in water. This simplifies the calculations:
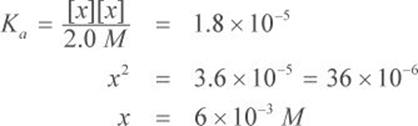
x represents the concentration of H3O+; therefore, [H3O+] = 6 × 10−3 M.
In this example, note that x is significantly lower than the initial concentration of acetic acid (2.0 M), which validates the approximation; otherwise, it would have been necessary to solve for x using the quadratic formula. Fortunately, the value of x on Test Day is almost always sufficiently small to make this approximation. A rule of thumb is that the approximation is valid as long as x is less than 5 percent of the initial concentration. This typically occurs when Ka is at least 100 times smaller than the concentration of the starting solution. For example, if Ka is 10−4 and the concentration of the starting solution is 0.01 M (10−2 M), then the ratio between the values is 102 or 100. The error in this calculation should be no more than ![]() On the other hand, if the Ka is 10−3 and the concentration is still 0.01 M, then the ratio between the values becomes 10, which could lead to
On the other hand, if the Ka is 10−3 and the concentration is still 0.01 M, then the ratio between the values becomes 10, which could lead to 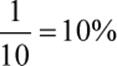 error. This degree of error may not be useful when identifying an answer choice on the MCAT.
error. This degree of error may not be useful when identifying an answer choice on the MCAT.
Students often feel nervous making the assumption that x is negligible because they want to see precise answer choices. However, keep in mind that the MCAT quite deliberately tests students’ ability to make reasonable assumptions under timed conditions to arrive at a feasible answer choice. Part of the skill of taking the MCAT is rounding appropriately to simplify math.
SALT FORMATION
Acids and bases may react with each other to form a salt and often (but not always) water, in what is termed a neutralization reaction. For example,
HA (aq) + BOH (aq) → BA (s) + H2O (l)
BRIDGE
Remember the reaction types discussed in Chapter 4 of MCAT General Chemistry Review? Go back and review the section on neutralization reactions if this equation doesn’t look familiar to you.
The salt may precipitate out or remain ionized in solution, depending on its solubility and the amount produced. In general, neutralization reactions go to completion. The reverse reaction, in which the salt ions react with water to give back the acid or base, is known as hydrolysis.
Four combinations of strong and weak acids and bases are possible:
· Strong acid + strong base: HCl + NaOH → NaCl + H2O
· Strong acid + weak base: HCl + NH3 → NH4Cl
· Weak acid + strong base: HClO + NaOH → NaClO + H2O
· Weak acid + weak base: HClO + NH3 → NH4ClO
The products of a reaction between equal concentrations of a strong acid and a strong base are equimolar amounts of salt and water. The acid and base neutralize each other, so the resulting solution is neutral (pH = 7), and the ions formed in the reaction will not react with water because they are inert conjugates.
The product of a reaction between a strong acid and a weak base is also a salt, but often no water will be formed because weak bases are often not hydroxides. In this case, the cation of the salt is a weak acid and will react with the water solvent, re-forming some of the weak base through hydrolysis. For example:
· Reaction I: HCl (aq) + NH3 (aq) → NH4+ (aq) + Cl− (aq)
· Reaction II: NH4+ (aq) + H2O (l) → NH3 (aq) + H3O+ (aq)
NH4+ is the conjugate acid of a weak base (NH3) and is stronger than the conjugate base (Cl−) of the strong acid, HCl. NH4+ will then transfer a proton to H2O to form the hydronium ion. The increase in the concentration of the hydronium ion causes the system to shift away from autoionization, thereby reducing the concentration of hydroxide ion. Consequently, the concentration of the hydronium ion will be greater than that of the hydroxide ion at equilibrium, and as a result, the pH of the solution will fall below 7. This should make sense: a strong acid and a weak base produce a slightly acidic solution.
On the other hand, when a weak acid reacts with a strong base, the pH of the solution at equilibrium will be within the basic range because the salt hydrolyzes, with concurrent formation of hydroxide ions. The increase in hydroxide ion concentration will cause the system to shift away from autoionization, thereby reducing the concentration of the hydronium ion. Consequently, the concentration of the hydroxide ion will be greater than that of the hydronium ion at equilibrium, and as a result, the pH of the solution will rise above 7. Consider the reaction of acetic acid, CH3COOH (weak acid) with sodium hydroxide, NaOH (strong base):
· Reaction I: CH3COOH (aq) + NaOH (aq) → Na+ (aq) + CH3COO− (aq) + H2O (l)
· Reaction II: CH3COO− (aq) + H2O (l) → CH3COOH (aq) + OH− (aq)
The pH of a solution containing a weak acid and a weak base depends on the relative strengths of the reactants. For example, the weak acid HClO has a Ka of 3.2 × 10−8, and the weak base NH3 has a Kb = 1.8 × 10−5. Thus, an aqueous solution of HClO and NH3 is basic because the Ka for HClO is less than the Kb for NH3. That is, HClO is weaker as an acid than NH3 is as a base. At equilibrium, therefore, the concentration of hydroxide ions will be greater than the concentration of hydronium ions in the aqueous solution.
In biology and biochemistry, neutralization reactions are often condensation reactions because they form bonds with a small molecule as a byproduct (usually water). The peptide bonds in proteins, for example, are created from the reaction of a carboxyl group (acid) and an amino group (base), while forming a water molecule, as shown in Figure 10.7. The salt in this reaction is the polypeptide itself; breaking it apart requires hydrolysis.
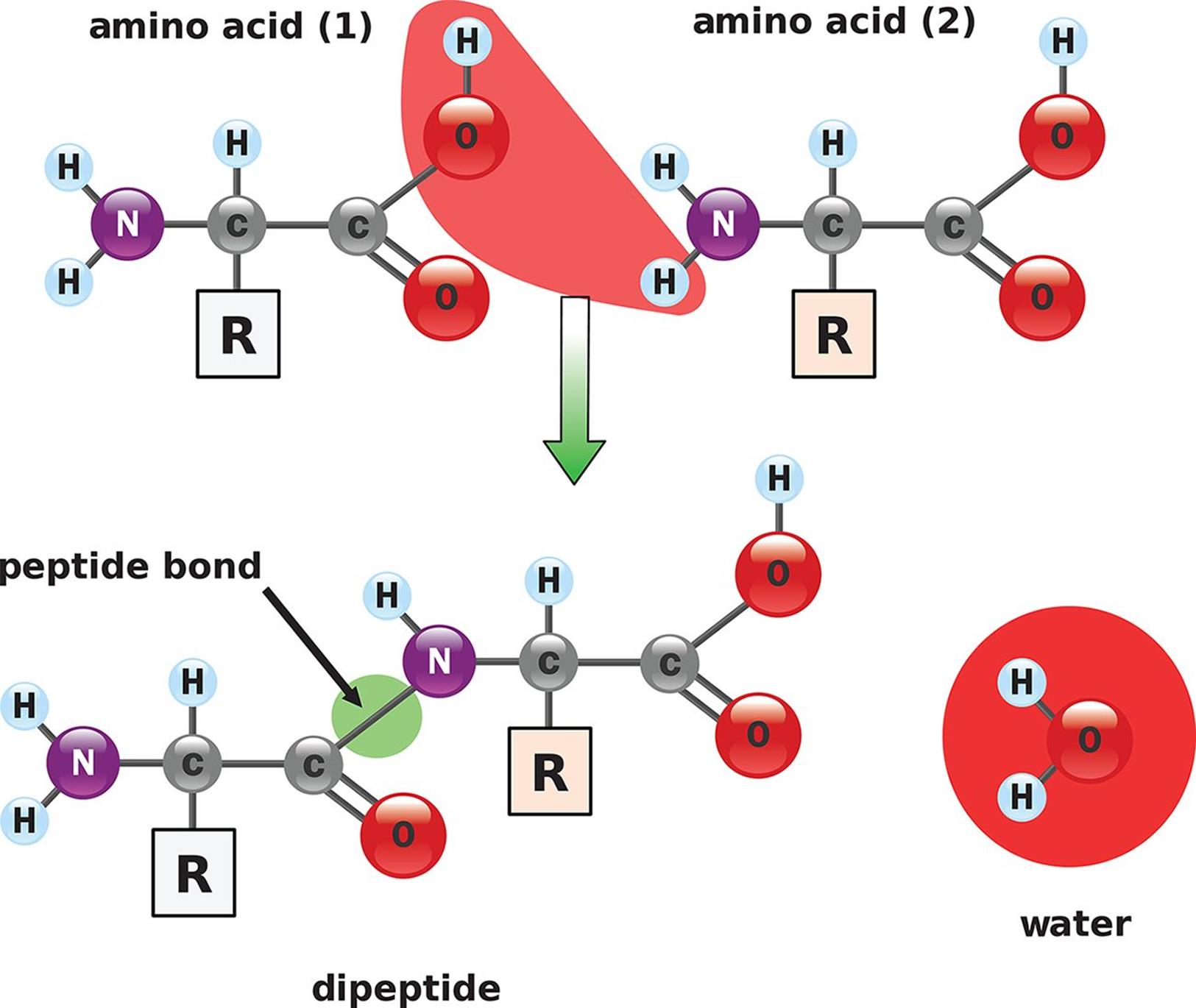 Figure 10.7. Peptide Bond Formation An acidic carboxyl group reacts with a basic amino group.
Figure 10.7. Peptide Bond Formation An acidic carboxyl group reacts with a basic amino group.
MCAT Concept Check 10.2:
Before you move on, assess your understanding of the material with these questions.
1. What is an amphoteric species?
2. If a compound has a Ka value ≫ water, what does it mean about its behavior in solution? How does this compare with a solution that has only a slightly higher Ka than water?
3. If a compound has a Kb value ≫ water, what does it mean about its behavior in solution? How does this compare with a solution that has only a slightly higher Kb than water?
4. Complete the blank cells in the table by utilizing the mathematical relationships between pH, pOH, and ion concentrations. (Note: Round the numbers given and use logarithmic approximations to determine p values, without a calculator, to simulate Test Day math.)
|
pH |
[H3O+] |
pOH |
[OH−] |
Acid or Base? |
|
4 |
||||
|
8.89 × 10−4 M |
||||
|
5.19 |
||||
|
1.88 × 10−6 M |
5. What is the mathematical relationship between Ka, Kb, and Kw?
6. Identify the conjugate acid–base pairings in the reactions below:

7. Determine the concentration of hydrogen ions and pH of a solution of 0.1 M acetic acid (Ka = 1.8 × 10−5).