Physical Chemistry: A Very Short Introduction (2014)

I have adopted the eyes of a physical chemist to lead you on an exploration of matter from the inside in Chapter 1, where the focus was on the properties of individual atoms and molecules. I have used them again to show how a physical chemist explores it from the outside in Chapter 2, where classical thermodynamics is aloof from any knowledge about atoms and molecules. There is, of course, a link between these notional insides and outsides, and the branch of physical chemistry known as statistical thermodynamics (or statistical mechanics) forms that bridge.

At this level of presentation, some will think that it is a bridge too far, for statistical thermodynamics, as its faintly fearsome name suggests, is very mathematical. Nevertheless, it is a central duty of science to show how the world of appearances emerges from the underworld of atoms, and I would omit a large chunk of physical chemistry if I were to evade this topic. I shall keep the discussion qualitative and verbal, but you should know that lying beneath the qualitative surface there is a rigid infrastructure of mathematics. Because I am stripping away the mathematics, and the soul of statistical thermodynamics is almost wholly mathematical, this chapter is mercifully short! You could easily skip it, but in doing so you would miss appreciating how some physical chemists think about the properties of matter.

The central point about statistical thermodynamics is that it identifies the bulk properties of a sample with the average behaviour of all the molecules that constitute it. There is no need, it claims, to work out the behaviour of each molecule, just as there is no need in certain sociological settings to follow the behaviour of an individual in a big enough sample of the population. Yes, there will be idiosyncrasies in molecular behaviour just as there are in human behaviour, but these idiosyncrasies, these ‘fluctuations’, are negligible in the vast collections of molecules that make up typical samples. Thus, to calculate the pressure exerted by a gas, it is not necessary to consider the impact of each molecule on the walls of a container: it is sufficient (and highly accurate given the large numbers involved, with trillions and trillions of molecules in even very small samples) to deal with the steady swarming impact of myriad molecules and to ignore the tiny fluctuations in the average impact as the storm abates or surges.

The Boltzmann distribution

There is one extraordinary conclusion from statistical thermodynamics that is absolutely central to physical chemistry and which accounts for great swathes of the properties of matter, including its reactions as well as illuminating that elusive property, temperature. If there is one concept to take away from this chapter, this is it.

One consequence of quantum mechanics is that an atom or molecule can exist only certain energy states; that is, its energy is ‘quantized’ and cannot be varied continuously at will. At the absolute zero of temperature, all the molecules are in their lowest energy state, their ‘ground state’. As the temperature is raised, some molecules escape from the ground state and are found in higher energy states. At any given temperature above absolute zero, such as room temperature, there is a spread of molecules over all their available states, with most in the ground state and progressively fewer in states of increasing energy.

The distribution is ceaselessly fluctuating as molecules exchange energy, perhaps as collisions in a gas, when one partner in the collision speeds off at high speed and the other is brought nearly to a standstill. It is impossible, given the many trillions of molecules in a typical sample, to keep track of the fluctuating distribution. However, it turns out that in such typical samples there is one overwhelmingly most probable distribution and that all other distributions can be disregarded: this dominant distribution is the Boltzmann distribution.

I will put a little more visual flesh on to this description. Suppose you had a set of bookshelves, with each shelf representing an energy level, and you tossed books at the shelves at random. You could imagine that in one set of tries you arrived at a particular distribution, maybe one with equal numbers on each of the shelves. Achieving that distribution is possible but highly unlikely. In another try, half the books land on the lowest shelf and the other half all on the top shelf. That, again is unlikely, but much more likely than the first distribution. (In fact, if you had 100 books and 10 shelves, then it would be about 2 × 10⁶³ times more likely!) As you went on hurling books, noting the distribution on each try, you would typically get different distributions each time. However, one distribution would turn up time and time again: that most probable distribution is the Boltzmann distribution.

Comment

So as not to complicate this discussion, I am leaving out a crucial aspect: that each distribution might correspond to a different total energy; any distribution that does not correspond to the actual energy of the system must be discarded. So, for instance, unless the temperature is zero, we reject the distribution in which all the books end up on the lowest shelf. All on the top shelf is ruled out too. Physical chemists know how to do it properly.

The Boltzmann distribution takes its name from Ludwig Boltzmann (1844–1906), the principal founder of statistical thermodynamics. Mathematically it has a very simple form: it is an exponentially decaying function of the energy (an expression of the form e^−E/kT, with E the energy, T the absolute temperature, and k the fundamental constant we now call Boltzmann’s constant). That means that the probability that a molecule will be found in a state of particular energy falls off rapidly with increasing energy, so most molecules will be found in states of low energy and very few will be found in states of high energy.

Comment

The Boltzmann distribution is so important (and simple) that I need to show a version of it. If two states have the energies E₁ and E₂, then at a temperature T the ratio of the numbers of molecules in those two states is

The reach of the tail of the decaying exponential function, its overall shape in fact, depends on a single parameter that occurs in the expression: the temperature, T (Figure 8). If the temperature is low, then the distribution declines so rapidly that only the very lowest levels are significantly populated. If the temperature is high, then the distribution falls off very slowly with increasing energy, and many high-energy states are populated. If the temperature is zero, the distribution has all the molecules in the ground state. If the temperature is infinite, all available states are equally populated. This is the interpretation of temperature that I mentioned: it is the single, universal parameter that determines the most probable distribution of molecules over the available states. This too is the beginning of the elucidation of thermodynamics through Boltzmann’s eyes, for temperature is the parameter introduced (as I indicated in Chapter 2 without going into details) by the Zeroth Law. We shall see below that Boltzmann’s insight also elucidates the molecular basis of the First, Second, and Third Laws.

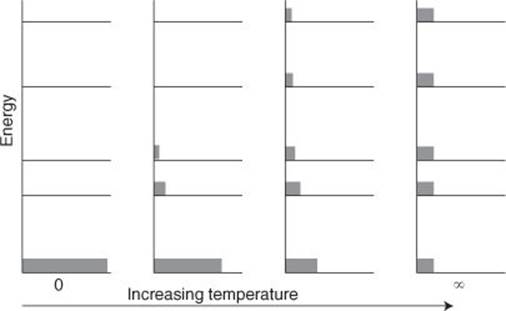
8. The Boltzmann distribution for a series of temperatures. The horizontal lines depict the allowed energies of the system and the tinted rectangles the relative numbers of molecules in each level at the stated temperature

The Boltzmann distribution captures two aspects of chemistry: stability and reactivity. At normal temperatures, the distribution implies that most molecules are in states of low energy. That corresponds to stability, and we are surrounded by molecules and solids that survive for long periods. On the other hand, some molecules do exist in states of high energy, especially if the temperature is high, and these are molecules that undergo reactions. Immediately we can see why most chemical reactions go more quickly at high temperatures. Cooking, for instance, can be regarded as a process in which, by raising the temperature, the Boltzmann distribution reaches up to higher energies, more molecules are promoted to states of high energy, and are able to undergo change. Boltzmann, short-sighted as he was, saw further into matter than most of his contemporaries.

Molecular thermodynamics

There is much more to statistical thermodynamics than the Boltzmann distribution, although that distribution is central to just about all its applications. Here I want to show how physical chemists draw on structural data, such as bond lengths and strengths, to account for bulk thermodynamic properties: this is where spectroscopy meets thermodynamics.

One of the central concepts of thermodynamics, the property introduced by the First Law, is the internal energy, U, of a system. As I pointed out in Chapter 2, the internal energy is the total energy of the system. As you can therefore suspect, that total energy can be calculated if we know the energy state available to each molecule and the number of molecules that are in that state at a given temperature. The latter is given by the Boltzmann distribution. The former, the energy levels open to the molecules, can be obtained from spectroscopy or by computation. By combining the two, the internal energy can be calculated, so forging the first link between spectroscopy or computation and thermodynamics.

The second link, a link to the Second Law, draws on another proposal made by Boltzmann. As we saw in Chapter 2, the Second Law introduces the concept of entropy, S. Boltzmann proposed a very simple formula (which in fact is carved on his tomb as his epitaph) that enables the entropy to be calculated effectively from his distribution. Therefore, because knowledge of the internal energy and the entropy is sufficient to calculate all the thermodynamic properties, from Boltzmann’s distribution a physical chemist can calculate all those properties from information from spectroscopy or the results of computation.

Comment

For completeness, Boltzmann’s formula for the entropy is S = k log W, where k is Boltzmann’s constant and W is the number of ways that the molecules can be arranged to achieve the same total energy. The W can be related to the Boltzmann distribution.

I am glossing over one point and holding in reserve another. The glossed-over point is that the calculations are straightforward only if all the molecules in the sample can be regarded as independent of one another. Physical chemists currently spend a great deal of time (their own and computer time) on tackling the problem of calculating and thereby understanding the properties of interacting molecules, such as those in liquids. This remains a very elusive problem and, for instance, the properties of that most important and common liquid, water, remain largely out of their grasp.

The point I have held in reserve is much more positive. Boltzmann’s formula for calculating the entropy gives great insight into the significance of this important property and is the origin of the common interpretation of entropy as a measure of disorder. When they consider entropy and its role in chemistry, most physical chemists think of entropy in this way (although some dispute the interpretation, focusing on the slippery nature of the word ‘disorder’). Thus, it is easy to understand why the entropy of a perfect crystal of any substance is zero at the absolute zero of temperature (in accord with the Third Law) because there is no positional disorder, or uncertainty in location of the atoms, in a perfect crystal. Furthermore, all the molecules, as we have seen, are in their ground state, so there is no ‘thermal disorder’, or uncertainty in which energy states are occupied.

Likewise, it is easy to understand why the entropy of a substance increases as the temperature is raised, because it becomes increasingly uncertain which state a molecule will be in as more states become thermally accessible. That is, the thermal disorder increases with temperature. It is also easy to understand, I think, why the entropy of a substance when its solid form melts and increases even more when its liquid form vaporizes, for the positional disorder increases, especially in the second case.

As we saw in Chapter 2, in thermodynamics, the direction of spontaneous change is that in which the entropy (the total entropy, that of the surroundings as well as the system of interest) increases. Through Boltzmann’s eyes we can now see that in every case the direction of spontaneous change, the ‘arrow of time’, is the direction in which disorder is increasing. The universe is simply crumbling, but such is the interconnectedness of events that the crumbling generates local artefacts of great complexity, such as you and me.

Molecular reactions

Physical chemists use statistical thermodynamics to understand the composition of chemical reaction mixtures that have reached equilibrium. It should be recalled from Chapter 2 that chemical reactions seem to come to a halt before all the reactants have been consumed. That is, they reach equilibrium, a condition in which forward and reverse reactions are continuing, but at matching rates so there is not net change in composition. What is going on? How do physical chemists think about equilibrium on a molecular scale?

In Chapter 2, I explained that physical chemists identify equilibrium by looking for the composition at which the Gibbs energy has reached a minimum. That, at constant temperature and pressure, is just another way of saying the composition at which any further change or its reverse results in a decrease in the total entropy, so it is unnatural. Because we have seen that statistical thermodynamics can account for the entropies of substances by drawing on structural data, we should expect to use similar reasoning to relate equilibrium compositions to structural data, such as that obtained from spectroscopy or computation.

The molecular reason why chemical reactions reach equilibrium is very interesting (I think) and is exposed by statistical thermodynamics. Let’s take a very simple, typical physical chemistry, reaction, in which A → B. We can use statistical thermodynamics to calculate the enthalpy and entropy of both the reactant A and the product B, and therefore we can use these values to calculate their Gibbs energies from structural data. Now imagine that all the A molecules are pinned down and can’t migrate from their starting positions. If the A molecules gradually change into B molecules the total Gibbs energy of the system slides in a straight line that reflects the abundances of the two species, from its value for ‘only A’ to the value for ‘only B’. If the Gibbs energy of B is less than that of A, then the reaction will go to completion, because ‘pure B’ has the lowest Gibbs energy of all possible stages of the reaction. This will be true of all reactions of the same form, so at this stage we should expect all such A → B reactions to go to perfect completion, with all A converted to B. They don’t.

What have we forgotten? Remember that we said that all the A were pinned down. That is not true in practice, for as the A convert into B, the A and B mingle and at any intermediate stage of a reaction there is a haphazardly mingled mixture of reactants and products. Mixing adds disorder and increases the entropy of the system and therefore lowers the Gibbs energy (remember that G = H − TS and its minus sign, so increasing S reduces G). The greatest increase in entropy due to mixing, and therefore the greatest negative contribution to the Gibbs energy, occurs when A and B are equally abundant. When this mixing contribution is taken into account, it results in a minimum in the total Gibbs energy at a composition intermediate between pure A and pure B, and that minimum corresponds to the composition at which the reaction is at equilibrium (Figure 9). The Gibbs energy of mixing can be calculated very easily, and we have already seen that the Gibbs energy change between pure A and pure B can be calculated from structural data, so we have a way of accounting for the equilibrium composition from structural data.

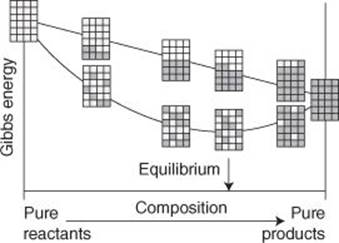
9. The role of mixing in the determination of the equilibrium composition of a reaction mixture. In the absence of mixing, a reaction goes to completion; when mixing of reactants and products is taken into account, equilibrium is reached when both are present

Similar reasoning is used by physical chemists to account for the effect of changing conditions on the equilibrium composition. As I remarked in Chapter 2, industrial processes, in so far as they are allowed to reach equilibrium (many are not), depend on the optimum choice of conditions. Statistical thermodynamics, through the Boltzmann distribution and its dependence on temperature, allows physical chemists to understand why in some cases the equilibrium shifts towards reactants (which is usually unwanted) or towards products (which is normally wanted) as the temperature is raised. A rule of thumb, but little insight, is provided by a principle formulated by Henri Le Chatelier (1850–1936) in 1884, that a system at equilibrium responds to a disturbance by tending to oppose its effect. Thus, if a reaction releases energy as heat (is ‘exothermic’), then raising the temperature will oppose the formation of more products; if the reaction absorbs energy as heat (is ‘endothermic’), then raising the temperature will encourage the formation of more product.

An implication of Le Chatelier’s principle was one of the problems confronting the chemist Fritz Haber (1868–1934) and the chemical engineer Carl Bosch (1874–1940) in their search in the early 20th century for an economically viable synthesis of ammonia (which I treat in more detail in Chapter 6). They knew that, because the reaction is exothermic, raising the temperature of their reaction mixture of nitrogen and hydrogen opposed the formation of ammonia, which plainly they did not want. That realization forced them to search for a catalyst that would facilitate their process at moderate rather than very high temperatures.

Statistical thermodynamics provides an explanation of Le Chatelier’s principle. (I remain focused on its role in explaining the effect of temperature: other influences can apply and be explained.) If a reaction is exothermic, then the energy levels of the products lie lower than those of the reactants. At equilibrium there is a Boltzmann distribution of molecules over all the available states, and if a molecule is in a ‘reactant’ state then it is present as a reactant, and if it is in ‘product’ state then it is present as a product. When the temperature is raised the Boltzmann distribution stretches up further into the high-energy reactant states, so more molecules become present as reactants (Figure 10), exactly as Le Chatelier’s principle predicts. Similar reasoning applies to an endothermic reaction, when the ‘product’ states lie above the ‘reactant’ states and become more populated as the temperature is raised, corresponding to the encouragement of the formation of products.

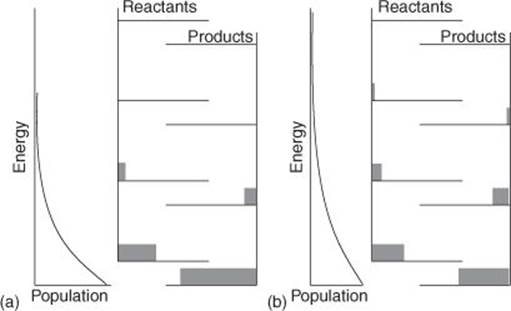
10. (a) At a given temperature there is a Boltzmann distribution over the states of the reactants and products; (b) when the temperature is raised in this exothermic reaction, more of the higher-energy reactant states are occupied, corresponding to a shift in equilibrium in favour of the reactants

A statistical perspective

I did warn that by stripping the mathematics out of the presentation statistical thermodynamics it might seem more vapour than substance. However, I hope it has become clear that this branch of physical chemistry is truly a bridge between molecular and bulk properties and therefore an essential part of the structure of physical chemistry.

In the first place, statistical thermodynamics unites the two great rivers of discussion, on the one hand the river of quantum mechanics and its role in controlling the structures of individual molecules, and on the other hand the river of classical thermodynamics and its role in deploying the properties of bulk matter. Thermodynamics, as I have stressed, can in principle stand aloof from any molecular interpretation, but it is immeasurably enriched when the properties it works with are interpreted in terms of the behaviour of molecules. Moreover, a physical chemist would typically regard understanding as incomplete unless a property of bulk matter (which includes the chemical reactions in which it participates) has been interpreted in molecular terms.

Second, physical chemistry is a quantitative branch of chemistry (not the only one, of course, but one in which quantitative argument and numerical conclusions are paramount), and statistical thermodynamics is right at its quantitative core, for although general arguments can be made about anticipated changes in energy and entropy, statistical thermodynamics can render those anticipations quantitative.

The current challenge

Statistical thermodynamics is difficult to apply in all except simple model systems, such as systems consisting of independent molecules. It is making brave attempts to conquer systems where interactions are of considerable and sometimes overwhelming importance, such as the properties of liquids (that enigmatic liquid water, especially) and of solutions of ions in water. Even common salt dissolved in water remains an elusive system. New frontiers are also opening up as very special systems come into the range of chemistry, such as biological molecules and nanoparticles. In the latter, questions arise about the relevance of large-scale statistical arguments, which are appropriate for bulk matter, to the very tiny systems characteristic of nanoscience.