Cracking the SAT Chemistry Subject Test

Part II

Subject Review

Chapter 11

Acids and Bases

In order to do well on the SAT Chemistry Subject Test, you'll need to know a few things about acids and bases, including what they are, how they behave in water, and how they react with each other.

Sometimes water molecules split apart to form H⁺ (a hydrogen ion) and OH⁻ (a hydroxide ion). An acid is anything that increases the H⁺ concentration of the solution; a base is anything that increases the OH⁻ concentration. How, why, and the degree to which this happens will be the focus of this chapter.

THE AUTOIONIZATION OF H₂O

This might surprise you, but a glass of water is not entirely composed of molecules of H₂O. Small amounts of H⁺(aq) and OH⁻(aq) are also present; these are formed during the spontaneous dissociation of water, a process called autoionization.

H₂O (aq) H⁺(aq) + OH⁻(aq)

Autoionization is reversible, and an equilibrium exists in which [H⁺], [OH⁻], and [H₂O] are stable.

This equilibrium can be upset by the addition of compounds that alter [H⁺] or [OH⁻], as predicted by Le Chatelier's principle. In fact, you'll see that aqueous acid-base chemistry is nothing new; it is simply the study of how other compounds introduced into solution can disturb the autoionization equilibrium of water.

Dissociation Constant for Water, K_w

The equilibrium expression for the autoionization of water is

K_w = [H⁺][OH⁻]

(Remember that H₂O doesn't appear in the equilibrium expression because it is the solvent.)

For pure water at 25°C, both [H⁺] and [OH⁻] are 10⁻⁷ M. Therefore, in pure water

K_w = [H⁺][OH⁻]

= (10⁻⁷ M)(10⁻⁷ M)

= 10⁻¹⁴ M² at 25°C

Furthermore, at constant temperature, regardless of whether more [H⁺] or more [OH⁻] is added to the solution, the K_w, or [H⁺] × [OH⁻], of any aqueous solution is equal to 10⁻¹⁴ M² at 25°C. That's because the only way to change the value of an equilibrium constant is to change the temperature of the solution.

What Is pH?

The [H⁺] of pure water at 25°C is 10⁻⁷ M. Many people find working with exponents, especially negative exponents, a bit scary. Luckily for you, the tradition of pH was conceived and created; pH and [H⁺] have the following relationship:

If [H⁺] = 10⁻⁷ M

then pH = −log(10⁻⁷) = 7

Note that “p” is the abbreviation for the numerical operation of –log; the –log is taken from whatever number follows the p. For example, given that

K_w = [H⁺][OH⁻] = 10⁻¹⁴ M²

taking the p of every term gives

pK_w = p[H⁺] + p[OH⁻] = 14

Notice that we don't include units here, so after taking the –log, the resulting number has no units.

Doing Log₁₀ in Your Head

For some people, having to figure out a base ten logarithm (log₁₀) is just as daunting as working with exponents. If you are one of these people, try the following trick:

Look at the number, and ask the question: “What's this number's exponent when it is written as a base ten number (in other words, 10 to some power)?”

For example

log 10⁴ = ?

Ask yourself, “What's the exponent of 10⁴ when it's written as 10? Well, it's already written as 10, so the answer is 4.

Try these.

log 10⁻⁸ =
log 1,000 =
log 0.01 =
log 1 =

The answers are −8, 3, −2, and 0, respectively.

But taking a logarithm of a number that isn't an even factor of 10 can seem tough. For example

log 58 = ?

Well, for this test, you can just make a good guess: 58 is between 10 and 100. Since log 10 = 1 and log 100 = 2, log 58 must be between 1 and 2.

And that's good enough for the SAT Chemistry Subject Test.

ACIDS AND BASES

Over the years, several different definitions for acids and bases have been introduced.

For example:

The Bronsted-Lowry definition is the one that's most widely used today, although it is commonplace for chemists to flip between the Bronsted-Lowry and Arrhenius definitions.

Bronsted-Lowry Acids and Bases

The most important thing to remember about the Bronsted-Lowry definition of acids and bases is that acids are proton donors and bases are proton acceptors. The term proton is used to mean H⁺(aq), and H⁺(aq) reacts with water to form the hydrodium ion, H₃O⁺(aq).

Most compounds behave either just as acids or just as bases no matter what other chemical species are in solution. However, a handful of molecules/ions can act as either acids or bases. They elect to either donate or accept H⁺(aq) in response to whatever else is in solution; these are calledamphoteric molecules/ions. One example of an amphoteric ion is the bicarbonate ion, HCO₃⁻(aq).

In acidic solutions, the following reaction occurs:

HCO₃⁻(aq) + H⁺(aq) → H₂CO₃(aq)

While in basic solutions, the following reaction takes place:

HCO₃⁻(aq) + OH⁻(aq) → CO₃²⁻(aq) + H₂O(l)

Strong Acids and Bases

Acids and bases that dissociate completely and stay dissociated are referred to as strong acids and bases. The term strong is NOT used as a common adjective in acid-base chemistry; it has a very specific meaning. It means completely dissociating. For example, HCl is a strong acid, and NaOH is a strong base.

HCl(aq) → H⁺(aq) + Cl⁻(aq)

NaOH(aq) → Na⁺(aq) + OH⁻(aq)

In the case of strong acids and bases, dissociation is considered 100 percent and irreversible, so a one-way reaction arrow is used in reactions of strong acids and bases. (Keep this in mind when you're asked to calculate the pH of strong acid-base solutions; it makes the math simpler.)

For the test, you MUST memorize the following list of strong acids and bases:

Calculating pH for Strong Acid or Base Solutions

We've said that strong acids and bases completely dissociate. This means that, for strong acids, [H⁺] equals the [STRONG ACID], and for strong bases, [OH⁻] equals the [STRONG BASE].

Example:

What is the pH of 1.0 M HNO₃(aq)?

Solution:

First, write the balanced chemical equation.

HNO₃(aq) → H⁺(aq) + NO₃⁻(aq)

Second, realize that there is really no HNO₃(aq) in solution; it has all dissociated. Therefore, what we really have is

HNO₃(aq) → H⁺(aq) + NO₃⁻(aq)

1.0 M 1.0 M 1.0 M

Third, since pH is the –log[H⁺], we get

pH = –log[H⁺]
= –log(1.0 M) = –log(10⁰ M)
= 0 

It's a good idea to remember that for a 1.0 M solution of any strong acid, pH = 0 because these solutions are commonly used in the SAT Chemistry laboratory questions. Don't make the mistake of thinking that –log(1) = 1!

Example:

What is the pH of 1.0 M KOH(aq)?

Solution:

First, write the balanced chemical equation.

KOH(aq) → K⁺(aq) + OH⁻(aq)

Second, realize that there is really no KOH(aq) in solution. It's all dissociated. Therefore, what we really have is

KOH(aq) → K⁺(aq) + OH⁻(aq)

1.0 M 1.0 M 1.0 M

Third, take the pOH since that's what we have.

pOH = –log[OH⁻]

= –log(1.0 M) = –log(10⁰ M)

= 0

Fourth, recall that pH + pOH = 14 (at 25°C), and solve for pH.

pH = 14 – pOH

= 14 – 0 = 14

It is also a good idea to remember that for 1.0 M strong base, pH = 14 because these solutions are also commonly used in the SAT Chemistry Test laboratory questions.

Weak Acids and Bases

Acids and bases that partially, reversibly dissociate are referred to as weak acids or bases. Again, the term weak is NOT used as a common adjective in acid-base chemistry. It has a very specific meaning; it means partial or reversible dissociation. For example, HF is a weak acid, and NH₃ is a weak base.

HF(aq) H⁺(aq) + F⁻(aq)

NH₃(aq) + H₂O(l) NH₄⁺(aq) + OH⁻(aq)

The reversible double-reaction arrow is used in weak acid-base dissociation reactions.

Being able to identify weak acids and bases will really help you on test day. No one memorizes the list of weak acids and weak bases because there are tens of thousands of them. The way to identify a weak acid or weak base is first to recognize whether a compound is acidic or basic, and then know that if it isn't in the set of the strong acids or strong bases, it must be weak.

Calculating pH for Weak Acids or Base Solutions

Weak acids and bases partially, reversibly dissociate. For this reaction, a dissociation constant, K_a for acids and K_b for bases, must be used to calculate the pH of a solution of weak acid or base.

Example:

Given that K_aHF = 7 × 10⁻⁴, what is the pH of 1.5 M HF(aq)?

Solution:

First, write the balanced chemical equation.

HF(aq) H⁺(aq) + F⁻(aq)

Second, write the equilibrium expression, so we can use K_aHF.

K_aHF =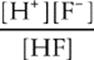

Third, write the algebraic expression (plug in numbers where you have them, and plug in letters where you don't).

(7 × 10⁻⁴) =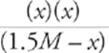

A couple of things about this last step: First of all, the reaction indicates that for every 1 HF molecule that dissociates, 1 H⁺ and 1 F⁻ are produced. That's why we used just x's in the algebraic expression instead of using three unrelated variables. Second of all, the equation above is actually a quadratic equation and can therefore be solved using the quadratic equation. However, in cases in which [HA] is at least 3 orders of magnitude (10³) larger than K_a, the fraction of HA lost due to dissociation is tiny and is completely ignored by chemists (this same rule applies for weak bases). So, for this problem, we can now write

(7 × 10⁻⁴) =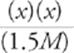

Fourth, solve the algebraic expression.

(7 × 10⁻⁴) =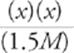

x² = (7 × 10⁻⁴) × (1.5 M) = 1 × 10⁻³

x = 1 × 10^−1.5

Fifth, don't worry about the fractional exponent because it will disappear when you calculate pH.

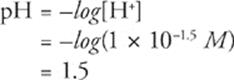
Try another example to make sure you've got it.

Example:

Given that K_b(NH3) = 1.8 × 10⁻⁵, what is the pH of 0.5 M NH₃(aq)?

Solution:

First, write the balanced chemical equation.

NH₃(aq) + H₂O(l) NH₄⁺(aq) + OH⁻(aq)

Second, write the equilibrium expression (use K_b(NH3)).

K_b(NH3) =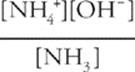

Third, write the algebraic expression (plug in numbers where you have them, and plug in letters where you don't).

(1.8 × 10⁻⁵) =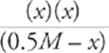

Since [NH₃] is at least 3 orders of magnitude larger than K_b(NH3), we can now write

(1.8 × 10⁻⁵) =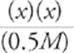

Fourth, solve the algebraic expression.

(1.8 × 10⁻⁵) =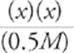

x² = (1.8 × 10⁻⁵) × (0.5 M) = 1 × 10⁻⁵

x = 1 × 10^−2.5

Fifth, don't worry about the fractional exponent because it will disappear when you calculate pOH.

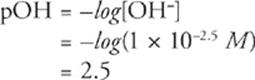
Sixth, remember that pH + pOH = 14 (at 25°C), and solve for pH.

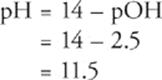
Na⁺ and NaOH

Na⁺(aq) can also be
thought of as Na(H₂O)⁺,
or simply remember that
aqueous metal ions are the
conjugates of their metal
hydroxides.

Conjugate Acid/Base Pairs

A conjugate pair of molecules refers to two molecules that have identical molecular formulas except that one of them has an additional H⁺.

Some examples of conjugate pairs are

HCl and Cl⁻
H₂O and OH⁻
H₂PO₄⁻ and HPO₄²⁻
Na⁺ and NaOH

Some molecules/ions that are often mistaken for conjugate pairs are

H₃O⁺/OH⁻, H₂SO₄/SO₄²⁻, H₂CO₃/CO₃²⁻

Since all of these differ by more than 1 H⁺, they do NOT qualify as conjugate pairs.

Now, the member of a conjugate pair that has an extra H⁺ is called the conjugate acid, and the member that has one fewer H⁺ is the conjugate base.

A word of caution: Just because a molecule is called conjugate acid or base does not mean it's actually acidic or basic in solution.

For example, given the conjugate pair

OH⁻/O²⁻

we see that by definition, hydroxide is the conjugate acid of the pair, but of course, OH⁻ is actually a base in solution.

Calculating Equilibrium Constants (K) for Weak Conjugate Acid/Base Pairs

Keep in mind that weak acids and bases do not completely ionize in aqueous solution. There is a measurable equilibrium, called the ionic equilibrium, between the weak acid and its conjugate base (or between the weak base and its conjugate acid). Here's a derivation that is pretty important to look through before test day. If you take any conjugate pair of a weak acid and weak base, such as NH₄⁺ and NH₃, writing out the balanced dissociation reactions in water for each gives the following:

For NH₄⁺(aq): NH₄⁺(aq) H⁺(aq) + NH₃(aq)

For NH₃(aq): NH₃(aq) + H₂O(l) NH₄⁺(aq) + OH⁻(aq)

Then, writing out the equilibrium expressions for each gives

For NH₄⁺(aq): K_aNH⁺₄ = [NH₃][H⁺] / [NH₄⁺]

For NH₃(aq): K_bNH3 = [NH₄⁺][OH⁻] / [NH₃]

Rearranging each so that [NH₄⁺] is by itself on the left yields

For NH₄⁺(aq): [NH₄⁺] = [NH₃][H⁺] /K_aNH⁺₄

For NH₃(aq): [NH₄⁺] = K_bNH3 [NH₃] / [OH⁻]

Now these can be set equal to one another as follows:

[NH₃][H⁺] / K_aNH⁺₄ = K_bNH3 [NH₃] / [OH⁻]

The [NH₃]'s cancel out, and then grouping the K's and concentration, respectively, leaves

(K_aNH⁺₄)(K_bNH3) = [OH⁻][H⁺]

Since we've already seen that [OH⁻] × [H⁺] = K_w = 10⁻¹⁴ M² at 25°C for any aqueous solution, then

(K_aNH⁺₄)(K_bNH3) = [OH⁻][H⁺] = K_w = 10⁻¹⁴ M², or

pK_aNH⁺₄ + pK_bNH3 = 14

In other words:

The sum of the pK_a and pK_b of a conjugate pair of a weak acid and weak base must always be equal to 14 at 25°C.

If the acid-base properties of one member of a conjugate pair are already known, then the acid-base properties of the other can be inferred using the conjugate rules. There are four conjugate rules that cover all of the possible combinations of strong/weak acids/bases.

1. The conjugate acid of a strong base is neutral.
Example: Na⁺ (the conjugate acid of NaOH) is neutral.

2. The conjugate base of a strong acid is neutral.
Example: Cl⁻ (the conjugate base of HCl) is neutral.

3. The conjugate acid of a weak base is an acid.
Example: NH₄⁺ (the conjugate acid of NH₃) is acidic.

4. The conjugate base of a weak acid is a base.
Example: F⁻ (the conjugate base of HF) is basic.

Memorize these conjugate rules. You'll need to know them in order to make sense of acid-base titration experiments.

Buffers

Buffers are solutions used to minimize (not prevent) a change in pH when an additional acid or base is introduced into solution. Buffers are made out of conjugate weak acids and bases—;the acid/base pair must be conjugates because if they weren't, they would immediately react, neutralize one another, and fail to establish a reversible reaction. Therefore, a buffer consists of a conjugate pair of a weak acid and weak base.

Calculating the pH of Buffers

Thanks to the algebraic skills of Henderson and Hasselbalch, calculating the pH of a buffer solution has been reduced to a relatively simple exercise in plug and chug. The most common version of the Henderson-Hasselbalch equation is

pH = pK_a + log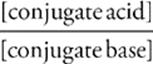

or

pH = pK_a + log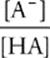

Unfortunately, people often remember this equation incorrectly, either because they're used to taking –logs in acid-base chemistry or because they're confused about whether [A⁻] or [HA] is in the numerator. So here is a test to check to make sure that the Henderson-Hasselbalch equation you jot down on test day is correct.

Adding a base to any solution, whether it is buffered or not, always increases the pH. The difference between a buffered and a normal solution is the size of the pH change. If we increase [A⁻] in our Henderson-Hasselbalch equation, then pH ought to increase.

pH = p K_a + log

Increasing [A⁻] makes the fraction bigger. Increasing a number also increases that number's logarithm, so + log is also bigger, and the pH has increased. We can see then that this is the correct equation. Adding a base increases the pH.

Of course, the Henderson-Hasselbalch equation can be worked out for pOH, as illustrated below.

pOH = pK_b + log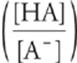

This passes the above test because increasing the amount of acid [HA] should always increase the pOH of any solution.

Example:

Given the K_{a(Acetic acid)} = 1.8 × 10^–5, what is the pH of a solution of 0.1 M acetic acid and 0.01 M sodium acetate?

Solution:

First, write the balanced chemical equation that establishes the equilibrium.

HC₂H₃O₂(aq) H⁺(aq) + C₂H₃O₂⁻(aq)

Of course, Na⁺ is ignored because the conjugate rules tell us that it doesn't affect pH in any way.

Second, write the relevant version of the

Henderson-Hasselbalch equation.

pH = pK_{a(Acetic acid)} + log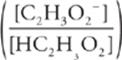

Third, covert the K_a to pK_a, and write the algebraic expression.

pH = 4.7 + log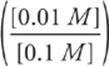

Fourth, solve it.

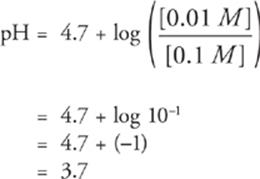
Some Final Facts About Buffers

Here's another look at the Henderson-Hasselbalch equation, but this time the concentration terms, M, are expanded into the equivalent (moles/V).

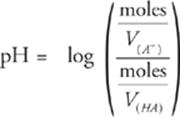
Since HA(aq) and A⁻(aq) are in the same solution, the volumes of both V_(HA) and V_(A⁻₎ must be equal. Therefore, volume cancels out, leaving

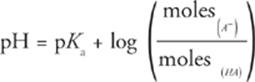
Examining this version of the Henderson-Hasselbalch equation reveals some additional properties of buffers.

1. If you're given the number of moles of HA and A⁻ in the test question, don't waste time converting to molarity just to plug into the Henderson-Hasselbalch equation; just use moles.

2. If the number of moles of HA and A⁻ are equal, then the Henderson-Hasselbalch equation can be simplified to pH = pK_a (or pOH = pK_b).

3. The pH of a buffer solution doesn't change with changing volume, since volume does not appear in the equation. Therefore, diluting or concentrating (through evaporation or osmosis) a buffer will not change its pH.

The third point is arguably the most important chemical property of a buffer, so memorize it.

Diluting or concentrating a buffered solution does not change its pH.

ACID-BASE TITRATIONS

An acid-base titration is an experimental technique used to acquire information about a solution containing an acid or base. Specifically, an acid-base titration can be used to figure out the following:

1. concentration of an acid or base

2. whether an unknown acid or base is strong or weak

3. pK_a of an unknown acid or pK_b of unknown base

All titration experiments are carried out in the same way. The procedure consists of adding a strong acid or base of known identity and concentration, called the titrant, to the unknown acid or base solution. The titrant is carefully added step-wise, and changes in pH are monitored and recorded. With each small sample of titrant, a fraction of the unknown base or acid molecules is neutralized and converted into their conjugates.

This procedure continues until either the pH of the solution starts to level off or a color change is observed using a pH indicator.

Analyzing a titration curve—;a curve obtained by plotting pH as a function of the volume of added titrant—;provides information about the unknown solution's concentration.

The Equivalence Point

The most important feature of any titration curve is the equivalence point. This is the point during the titration where just enough titrant (in moles) has been added to completely neutralize the subject acid or base. At the equivalence point, no unreacted titrant or unknown base/acid remains in solution. Keep in mind that conjugate acids and bases need not be neutral (recall the conjugate rules). Therefore, do not make the mistake of automatically associating the equivalence point with pH 7.

Different Ways to Say It

The equivalence point is
also called the inflection
and the end point.

You can locate the equivalence point by eyeballing the titration curve: It is the point at which the curve is the steepest.

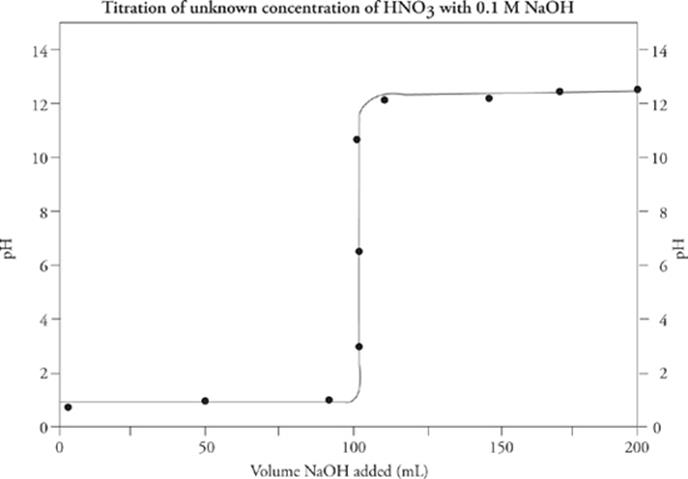
Determining Concentration

As we said earlier, the equivalence point is that point in the titration where just enough titrant has been added to completely neutralize the unknown acid or base. Therefore, since the number of moles must be equal at the equivalence point, if we know the concentration of the titrant, and the amount of the titrant we've added, we can calculate the concentration of the unknown solution, using an adaptation of the dilution equation, M_iV_i = M_fV_f.

Molarity_(subject) × Volume_(subject) = Molarity_(titrant) × Volume_(titrant)

Rearranging this to solve for Molarity_(subject) gives

Molarity_(subject) = (Molarity_(titrant) × Volume_(titrant)) / Volume_(subject)

Therefore, for the titration curve we just saw

Molarity_(HNO3) = (0.1 M × 100 mL) / 100 mL

= 0.1 M

The concentration of HNO₃ was 0.1 M.

In a titration, the pH at the equivalence point indicates whether the unknown acid or base is strong or weak. If the pH at the equivalence point is exactly 7, then the unknown acid or base is strong. If the pH at the equivalence point is greater or less than 7, the unknown acid or base is weak.

This is true because all of the acid/base and added titrant have been neutralized into their conjugates at the equivalence point. Remember the conjugate rules: The conjugates of strong acids and bases are neutral, while the conjugates of weak acids and bases are in fact basic and acidic, respectively.

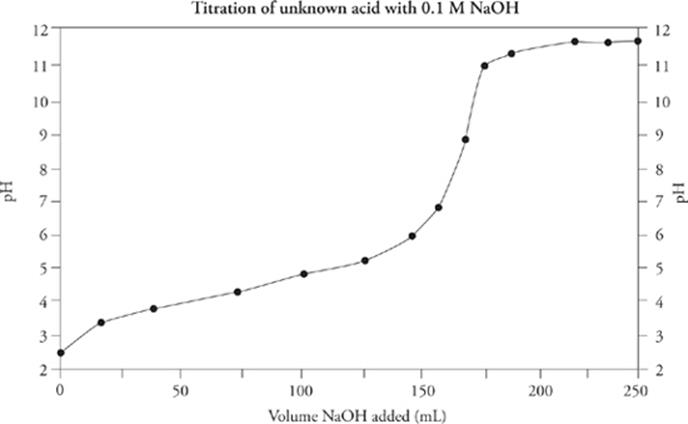
Since the equivalence point for this titration curve lies above pH = 7 (around pH = 9), and the titration was done using an NaOH solution as the titrant, the original solution contained a weak acid.

Determining pK_a (pK_b)

First, a warning: NEVER try to figure out the pK_a or pK_b of a strong acid or base—;they react completely.

Now, figuring out the pK_a of a weak unknown acid (or pK_b for a weak unknown base) requires finding a second location on the titration curve: the half-equivalence point. The half-equivalence point, as its name suggests, is the point at which enough titrant has been added to neutralize exactly one-half of the original unknown acid or base. You can identify this point by locating the equivalence point and then backtracking halfway to zero along the x-axis.

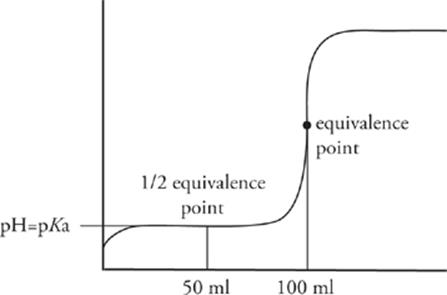
The half-equivalence point is an important location on the titration curve because at this point, equal amounts of the unknown acid or base and its conjugates exist in the solution. That means the solution is a buffer, so the Henderson-Hasselbalch equation applies.

For titration of weak acid with strong base:

pH = pK_a + log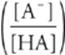

For titration of weak base with strong acid:

pOH = pK_b + log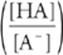

Furthermore, since [A⁻] = [HA] at the half-equivalence point, the Henderson-Hasselbalch equation simplifies to the following:

For titration of weak acid with strong base:

pH_{(at the half-eq point)} = pK_a

For titration of weak base with strong acid:

pOH_{(at the half-eq point)} = pK_b

Therefore, the solution's pH at the half-equivalence point is actually the pK_a of the unknown weak acid. For a weak base, the pK_b can be quickly calculated as follows:

pK_b = pOH_{(at the half-eq point)} = 14 – pH_{(at the half-eq point)}

For the titration curve we just showed, the unknown weak acid has a pK_a = 4.5.

Acid-Base Indicators

An indicator is just the conjugate pair of a weak acid or base, where each conjugate is a different color. Here's an example:

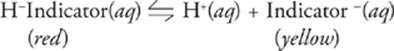
Since only a trace amount of an indicator is used in a titration, the acid-base dissociation doesn't impact the solution's overall pH. Instead, the indicator's dissociation equilibrium is shifted one way or another depending upon the solution's pH, according to Le Chatelier's principle. If the indicator above were used in a titration, then in acidic solutions, the indicator would be driven to the conjugate acid form (red), and in basic solutions, it would be driven to the conjugate base form (yellow).

All you really need to know for this test is that a chemical acid-base indicator is a substance that changes color in a pH range ±1 of its pK_a.

For example, thymol blue, which has a pK_a = 2, undergoes a red-to-blue color change in the pH range 1 to 3. Also, litmus paper changes color at about pH 7. At pH's lower than 7, the paper is red, while at pH's greater than 7, the paper is blue. Keep these things in mind when selecting an appropriate chemical indicator.

Incidentally, the test writers will want you to know how we add acid to base or base to acid, and the answer is to use a buret. A buret is a little measuring device that allows us to drop small, known amounts of liquid into a container.

Review this section on acids and bases, and then try the following questions. Answers can be found in Part III.

Question Type A

Questions 17–20 refer to the following.

(A) HBr (aq)

(B) NH₃ (aq)

(C) H₂O (l)

(D) HF (aq)

(E) H₂CO₃ (aq)

17. A strip of litmus paper will appear blue in it

18. At 25°C, it has a pH > 7

19. Is essentially a nonelectrolyte

20. Its aqueous ionization goes virtually to completion

Question Type B

110.

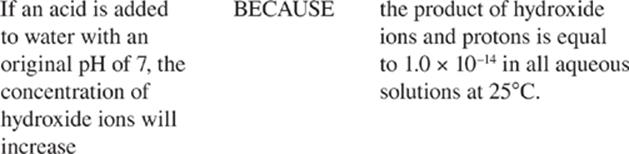
111.

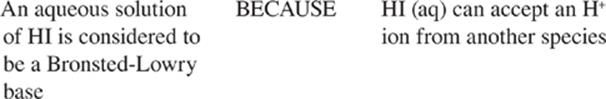
Question Type C

50. HNO₃ (aq) + OH^– (aq) H₂O (l) + NO₃^– (aq)

In the reaction above, which species is the conjugate acid?

(A) HNO₃(aq)

(B) OH^–(aq)

(C) H₂O(l)

(D) NO₃^–(aq)

(E) There is no conjugate acid in the above reaction.

53. A titration experiment is conducted in which 15 milliliters of a 0.015 M Ba(OH)₂ solution is added to 30 milliliters of an HCl solution of unknown concentration and titration is complete. What is the approximate concentration of the HCl solution?

(A) 0.015 M

(B) 0.03 M

(C) 1.5 M

(D) 2.5 M

(E) 3.0 M

55. Which is true regarding an aqueous solution of H₃PO₄ at 25°C?

(A) It has a very large acid ionization constant.

(B) It has a bitter taste.

(C) The concentration of [OH^–] > 1.0 × 10^–7 M.

(D) It is a weak electrolyte.

(E) It can be formed by the reaction of a metal oxide and water.

Summary

· In any aqueous solution, the product of the H⁺ and OH⁻ concentrations will equal 1 × 10^–14 at 25 degrees Celsius.

· The pH and pOH of a solution are given by

pH= –log([H⁺]) pOH = –log([OH⁻])

· pH + pOH = 14

· An Arrhenius acid is anything that produces H⁺, and an Arrhenius base is anything that produces OH⁻.

· A Lewis acid accepts a pair of electrons in solution, and a Lewis base donates a pair of electrons.

· A Bronsted-Lowry acid is a proton donor, and a Bronsted-Lowry base is a proton acceptor.

· Strong acids and strong bases completely and irreversibly dissociate.

· To calculate the pH of a strong acid, simply calculate the molarity of the solution. Because every acid molecule produces 1 H⁺, the molarity equals the H⁺ concentration, and can be used to find pH.

· Weak acids and weak bases partially and reversibly dissociate.

· To calculate pH for a weak acid, use the equation

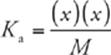
where x is the H⁺ concentration, and M is the molarity of the solution. Solve for x, and then convert to pH.

· After one H⁺ has been removed from an acid molecule, the molecule that remains is the conjugate base.

· For any conjugate acid base pair:

pK_a + pK_b = 14.

· A buffer is a solution of a weak acid/base conjugate pair that resists changes in pH when other acids or bases are added.

· The pH of a buffer is given by the Henderson-Hasselbalch equation:

· In a titration, molarity_(acid) × volume_(acid) = molarity_(base) × volume_(base).

· The equivalence point in the titration of a strong acid or base is always at a pH of 7.

· The equivalence point in a titration is above 7 for a weak acid and below 7 for a weak base.

· In the titration of a weak acid or base, the pH halfway to the equivalence point, or the half-equivalence point, gives the pK_a or pK_b.